前言
前段时间一直在负责某个项目的debug工作,其中一个问题的核心原因是接收电路的输入失调电压过大造成,该接收电路是以op为核心器件构建的信号链电路,负责对信号进行放大、均衡等。这次debug经历让我对失调有更深入的理解之外,也让我认识到自己到失调知识的理解是碎片化的,因此这篇文章主要目的是梳理一下个人对失调的理解,争取有系统性的理解。
作为经验总结性文章,争取用通俗易懂的语言来表达。对于总结过程中提到的内容,如果教科书上有详细介绍的,这里就不再抄书了,毕竟抄书是一件无趣又费时间的事情。此外,为了避免漫无目的地谈论一个话题的无效情景,应该聚焦一个话题展开,且这个话题应该围绕某类具体的电路的来探讨失调。这样的电路不多,我认为选择运放是一个较好的选择,这是基于以下几个原因:
- OP是vwin 电路中最常见的电路,工程中出现频次极高;
- 很多关注失调大小的电路如LDO、ADC等电路,都往往与OP有关;
- OP作为核心电路之一,可获取的资料最多,便于查阅;
因此,本文将主要以OP为例分析其失调电压的影响因素,然后从设计角度给出优化失调的方法。
几个名词
在开始之前,有必要对几个名词做一番解释,如“失调”、“失配”、“匹配”等词。
“失调”和“失配”是两个很容易混淆的词汇,虽然只有一字之差,但表达的含义却完全不同。失配mismatch是芯片工艺加工过程中存在的客观非理想因素,不管工艺如何先进,失配都是存在的。比如两个紧邻的输入对管,尽管我们设计地一样,它们的W和L并不会完全一致、每个管子的掺杂浓度也有差异、它们的栅的光滑程度也不一样。这就像“世界上没有完全相同的两片树叶”一样,任何你期望达到理想匹配的器件总会带有瑕疵,这些瑕疵可以称为“失配”。从这个角度而言,实际制造过程中的偏差以失配呈现在我们眼前。
接下来我们说下“匹配”,因为存在失配,所以我们在版图布局时,会在物理位置的摆放上思考更多,尽量争取用更合理的摆放位置来使两者失配的影响最低。因此就有了诸如书上说的一维匹配、共质心匹配等匹配技术。所以,“匹配”是一种手段,是以物理的方式减弱失配的影响,匹配技术是模拟电路版图设计艺术性的一个重要体现方面。
“失调则是一个参数名词,比如有“失调电压”、“失调电流”等。那么“失调”和“失配”之间存在什么关系呢?答案是:失配是产生失调的充分非必要条件。简单来说,就是有失配一定产生失调,但有失调却不一定存在失配(或者没有失配也有可能产生失调)。
前半句是好理解的,这里解释下后半句,为什么说即使没有失配也有可能存在失调呢?就拿简单的五管运放、电流镜电路来说,他们首先存在结构性的不匹配,也就是说结构本身就不对称,对于这种电路,即使不存在失配mismatch,他们也是存在失调电压的。教科书上对刚描述的情况都有提及,这里不再搬运内容了。总之,这种失调又被称为“系统失调”,属于系统误差,说白了就是结构性不对称导致的失调,解决这类失调,只要采取对称结构,就可以消除结构性失调,即消除系统失调。
那对于全对称结构而言,虽然没有了系统失调,但失配mismatch仍会导致“不对称”,这就像前面说的“世界上没有完全相同的两片树叶”一样,你认为的一样和对称只是你认为的。为什么呢?举一个简单的例子,假设没有失配,同样偏置下的两个尺寸相同的MOS管,其输出电流肯定是完全相同的,假设都为a,其输出电流的差异为0,如果以输出失配电流来衡量的话,那么此时的失配电流为0,也可以说没有失调电流。但真实的情况是,一只输出电流为a,另一只为a+x(x≠0),这时候有了差异,差异以x大小呈现,此时的失调电流为x。
好了,前言到此结束,接下里开始核心内容。本文将从以下几个方面进行展开:
- 什么是运放的失调电压,它是怎么定义的?
- 失调电压是怎么产生的?
- 一个简单全差分OP输入失调大小计算的例子
- 复杂结构的失调计算技巧
什么是运放的失调电压,它是怎么定义的?
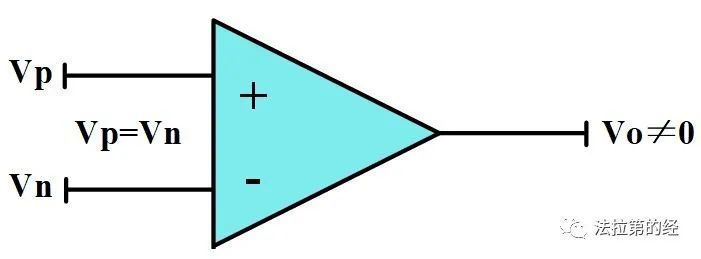
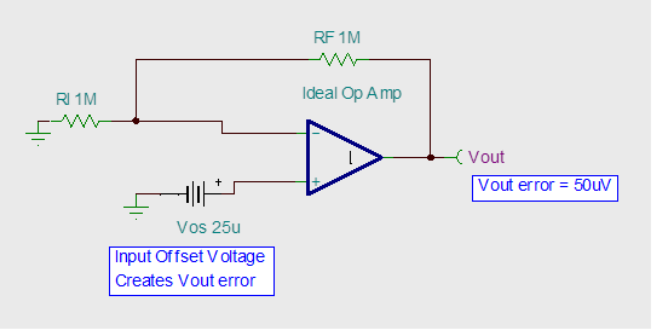
对于一个理想的全差分运放,当差分输入Vin=0时,其差分输出Vout=0,然而在实际运放中这是不可能实现的。举个例子,如果我们有一个真实的运放,当Vin=0时,你会发现其Vout≠0,接着当你慢慢改变Vin的值,终于在某个值,比如Vin=10mV时Vout变为了0,那么此时的Vin值即为运放的输入失调电压,一般用Vos表示。也就是说,你手里的这个实际运放的输入失调电压Vos=10mV。
也就是说,全差分OP的失调电压可以这么定义:可以使差分输出等于0时对应的差分输入即为失调电压。
那对于单端运放,失调应该怎么定义呢?书上一般是这么说的:可以使差分输出等于vdd/2时对应的差分输入即为失调电压。这里的“vdd/2”不应该做僵化的理解,其实可以认为是不考虑mismatch时的输出DC值,它是一个基准值,有失配时输出肯定不等于基准值,而能令输出回归到基准值的输入即为失调电压,所以单端运放的定义可以是:可以使输出等于设定的基准值时对应的输入即为失调电压。
失调电压是怎么产生的?
其实,这个问题在前言部分也有所提及。对于全差分OP而言,失调是因为失配而产生的。我们知道,全差分OP是全对称的,但在真实的物理世界,尤其是每只管子都是在带有随机制造误差的产线上加工出来的,因此“全对称”只是理念上的产物,实际是不存在的。
虽然说失配的存在使全差分只在理想上对称,但这样的结构在抵抗失配影响方面比起单端电路而言仍然具备极大优势。虽然说客观世界上的失配无法避免,但为了做出更优秀的电路,很多人还是为此在不断努力。这样的努力是体现在多方面的,比如工艺工程师不断优化加工精度,减小随机误差的影响;IC设计工程师则分析某种电路在参数性能上是如何受失配影响的,他们通过设计更大的W/L、控制管子的驱动电压或者gm的等方式来尽可能抵抗失配对性能的影响。
其实对作为模拟IC设计师的人们而言,如果选择通用工艺,那么让工艺厂在减小失配方面做更大努力是比较困难的,因此主要还是在设计上发力。既然这样,针对某种常用结构进行失配影响的分析就显得很有必要了,当我们知道失配对性能的限制之后,我们就有方法通过合理的设计来减小失配的影响。
接下来我们找一个全差分OP来进行失配影响分析。
一个简单全差分OP输入失调大小计算的例子
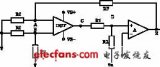
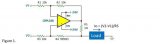
在Razavi的书中,对一个电阻负载的的差分OP进行了失调计算,其结构如下所示:

书上已给出了该结构的Vos,in的计算过程,十分详细,这里不再抄一遍,毕竟抄书是一件无趣的事情。更有价值的是看到这个计算过程背后的一些思想,它可以给我们带来关于分析方法上的思考:
- 以 定义作为计算的切入点,即找到一个Vos,in值,使输出Vout=0;
- 器件不匹配的体现方法:左一半,VTH1=VTH,(W/L)1=W/L, R1=RD,ID1=ID;右一半,VTH2=VTH+△VTH,(W/L)2=W/L+△(W/L), R1=RD+△RD, ID1=ID+△ID;浓缩成一个原则就是:左边的值=标准值,右边的值=标准值+△。
- 忽略次要因素,如λ = γ = 0, μnCox的失配;
- 计算过程中将非线性部分,如根式用泰勒近似得到多项式形式,且忽略两小量乘积项(如△1*△2被忽略),以便得到能够对设计有指导意义的表达式。
对于上图所示的运放,将Vos,in的结果整理如下:

观察上面式(2),负载电阻的失配和晶体管尺寸失配随驱电压Vov的增大而增大;而VTH的失配则直接折合到输入。
对最终公式的的思考:
(1)为了减小Vosin,需要减小Vov,如果电流一定的情况下,则需要增加W/L,假设L保持不变,则需要增加W尺寸,这样一来Vov减小的同时W/L的失配其实也减小了。我们还知道,阈值VTH失配和W*L成反比,因此阈值失配也会减小。而且,Vov↓同时gm↑,也是实现更低噪声、更大的增益、更宽的输出摆幅和共模输入范围、更高的CMRR和PSRR所希望的。当然这里也有折中,实际上Vov要与放大器频率特性相互折衷,例如MOS管自身的本征频率fT是与Vov成正比的。
(2)RD的失配也是可以考虑减小的。RD一般是工艺电阻,保持阻值不变(即L/W不变)的同时可以考虑同比增大L和W,这样有益于降低电阻失配。

复杂结构的失调计算技巧
上面的公式(1)是一个很重要的结果,这个结果虽然是从R负载的全差分OP得到的,但对于更复杂的全差分OP的输入失调计算中仍然会反复利用到该公式,这一点倒并不意外。有些时候我们可以将简单结构看成是复杂结构的简化版,或者说复杂结构其实也是从某简单结构演变而成,本质的拓扑是相同的。从已有结论扩展到复杂结构的计算,无疑可以省却大量的计算过程。
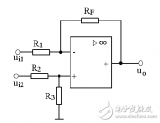
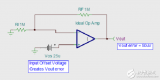
Razavi书上的另一个例子就是电流源负载形式的全差分OP,其结构如下:

计算得到的Vos,in如下

根据公式揭示的信息,在设计上可以按照下面的思路进行失调优化:
- N管Vov取小,W和L可考虑同比扩大。好处:W/L本身失配减小,且受更小的过驱电压衰减、阈值失配也减小、gmn增大,更有益于衰减负载管失调;
- P管的Vov取小,大括号里W/L失配影响减小,但gmp反而会增加。所以我认为设计时首先可以根据gmn大小选择gmp的大小,确定gmp/gmn的衰减比。偏置电流一定时,倒推确定P管的Vov,然后尽量选取大的W和L,以直接减小W/L失配和阈值失配。
下面是这个例子的计算背后的一些经验性思考:
首先,Vos,in包含了所有负载管和对管的失调。书上在计算时,使用到了叠加法的原则,这个原则的应用是十分广泛的。在这个例子里,在计算输入对管的失调时,先假定负载管是理想的;等到计算负载管引入的失调时,则假定对管是理想的,最后只需要将计算得到的两个结果相加即可得到最终结果。能够应用叠加法的前提是认为负载管的失配和对管的失配是两个完全独立的因素,它们之间没有相互影响。在其他场合要使用叠加法时也需要思考一下这个前提是否存在。
其次,式(3)中Vosn、Vosp是其实直接利用了公式(1),只是因为应用叠加法的两次计算中△ID=0,因此这里收过驱电压影响的因素只有W/L失配。为什么这个例子中计算时认为△ID=0?(显然和前一个例子不同),这是因为计算对管失配时,负载管是理想的,所以I3=I4,左右两侧电流不存在失配。同样在计算负载管失调时,输入对管理想,所以I1=I2,左右两侧电流也不存在失配。
最后,是“折算”的方法。虽然我们能够计算出负载管失调Vos,p,但需要将其折算到输入级去。之所以进行这样的折算是因为我们关注的是输入参考失调。对于为什么要折算,我有点个人的理解。在实际层面,显然每个管子的失配最终引起的是输出结果Vout≠0(当Vin=0时),这时的值为Vos,out。为了在数学形式上的简介和理想模型的有效性,富有智慧的人们引入了“折算”概念,即将Vos,out除以gain得到Vos,in,称其为输入参考失调电压。这完全是数学的处理。我想人们总要考虑到某些优点才会别出心裁这么处理的,因为这么处理之后,就可以将一个实际OP等效成(或建模成)一个输入存在Vos,in的理想OP。这么等效之后,在所有其他的计算中,可以将Vos,in与Vin相加得到新输入Vin,new,而OP仍可以视作理想的。

具体折算时,和噪声的处理技巧一样,Vos,p乘以gmp换算为电流,然后再除以gmn等效成输入电压,即Vos,p*gmp/gmn。
这篇文章就先到这里。其实在写这篇文章的过程中,感觉还有很多内容可以写,比如为什么bjt工艺的失调会比cmos工艺的失调好?更复杂的运放结构在计算失调时应该怎么考虑?一个工艺的失调可以通过什么方式来评估?等等。这些问题争取在后续的文章中给出回答。
 德赢Vwin官网
App
德赢Vwin官网
App























评论