德赢Vwin官网
App
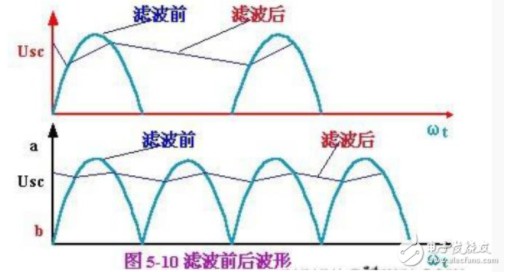
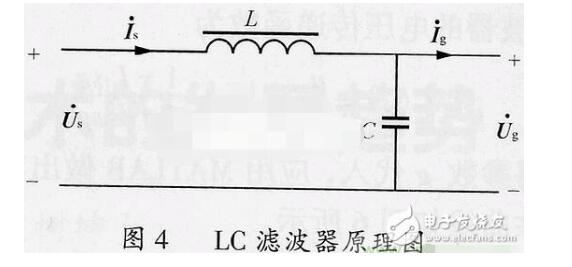
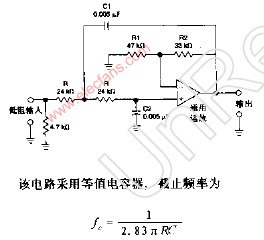
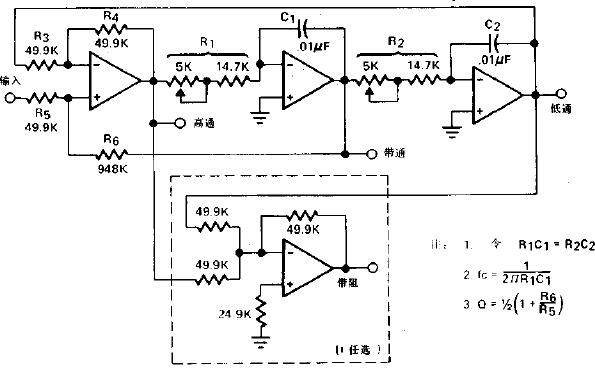
滤波是信号处理中非常重要的一个步骤，常用器件就是滤波器，滤波使输出电压纹波系数降低，波形变得比较平滑。滤波器的阶数可分为一阶、二阶和高阶，阶数越高，幅频特性越陡峭，高阶滤波器通常可由一阶和二阶滤波器级联而成。
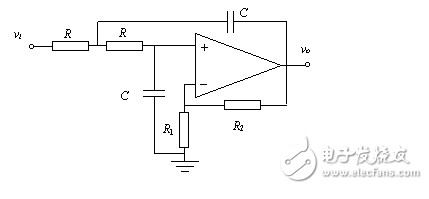
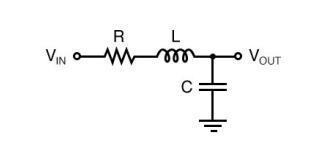
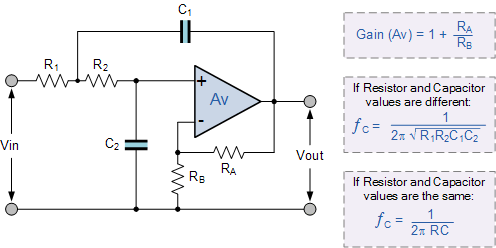
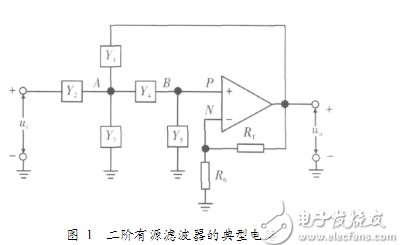
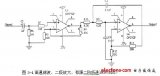
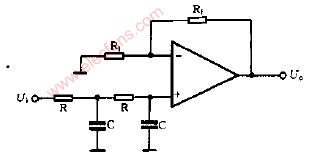
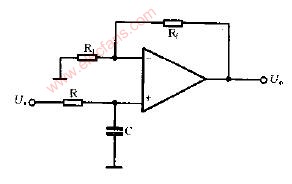
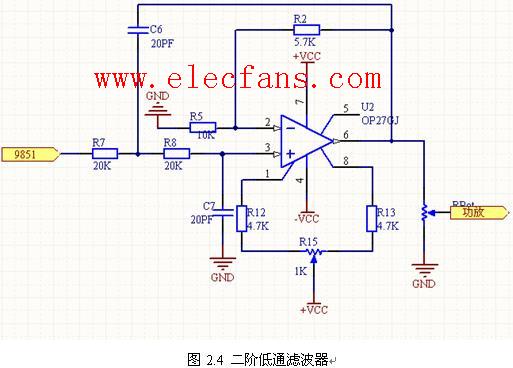
如上图所示：二阶低通滤波器电路图
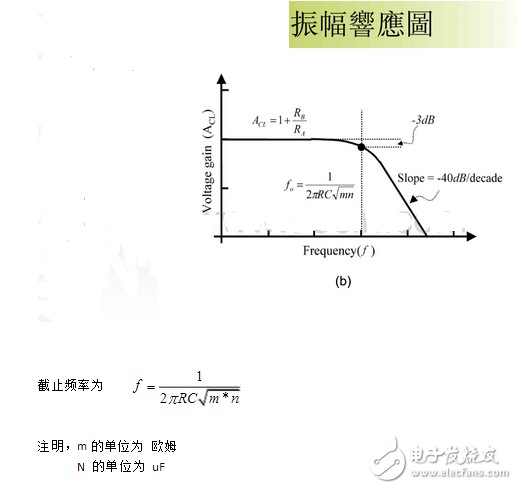
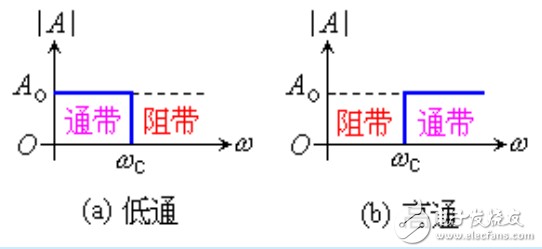
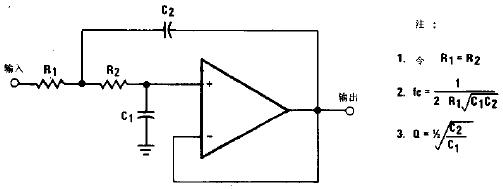
品质因数表明了滤波器通带的状态。一般要求Q=0.707。
由此可以得到
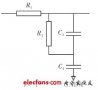
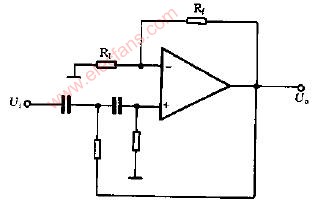
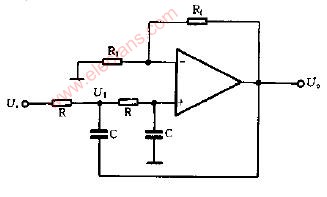
常用二阶低通滤波器电路图
最常用的3种二阶有源低通滤波电路为：
巴特沃兹，最平滑；
切比雪夫，迅速衰减，单通带中有纹波；
贝塞尔，相移与频率成正比，群延时基本是恒定。
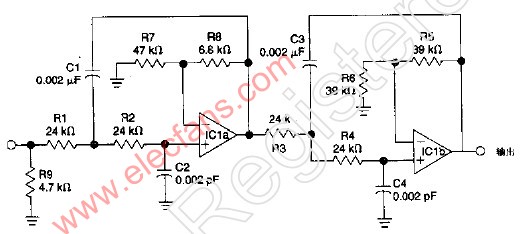
巴特沃斯滤波器
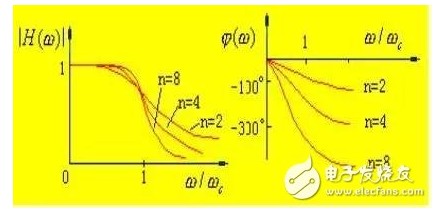
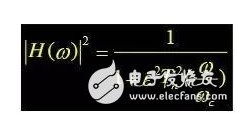
从幅频特性提出要求，而不考虑相频特性。巴特沃斯滤波器具有最大平坦幅度特性，其幅频响应表达式为：
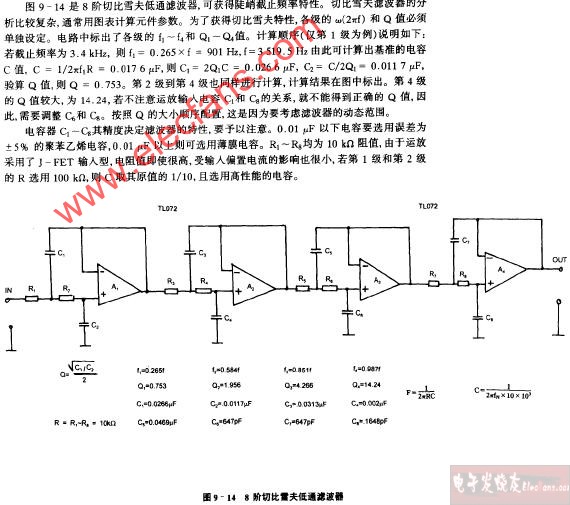
切贝雪夫滤波器
切贝雪夫滤波器也是从幅频特性方面提出逼近要求的，其幅频响应表达式为：
ε是决定通带波纹大小的系数，波纹的产生是由于实际滤波网络中含有电抗元件；Tn是第一类切贝雪夫多项式。
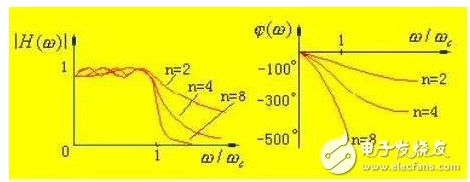
与巴特沃斯逼近特性相比较，这种特性虽然在通带内有起伏，但对同样的n值在进入阻带以后衰减更陡峭，更接近理想情况。ε值越小，通带起伏越小，截止频率点衰减的分贝值也越小，但进入阻带后衰减特性变化缓慢。
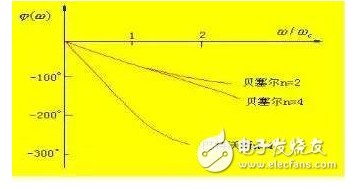
切贝雪夫滤波器与巴特沃斯滤波器进行比较，切贝雪夫滤波器的通带有波纹，过渡带轻陡直，因此，在不允许通带内有纹波的情况下，巴特沃斯型更可取；从相频响应来看，巴特沃斯型要优于切贝雪夫型，通过上面二图比较可以看出，前者的相频响应更接近于直线。
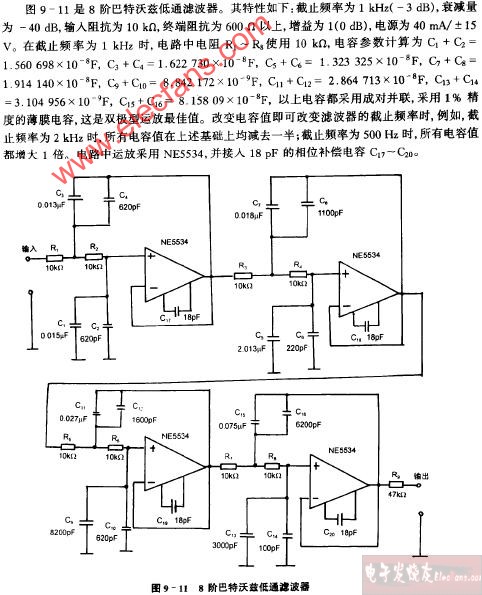
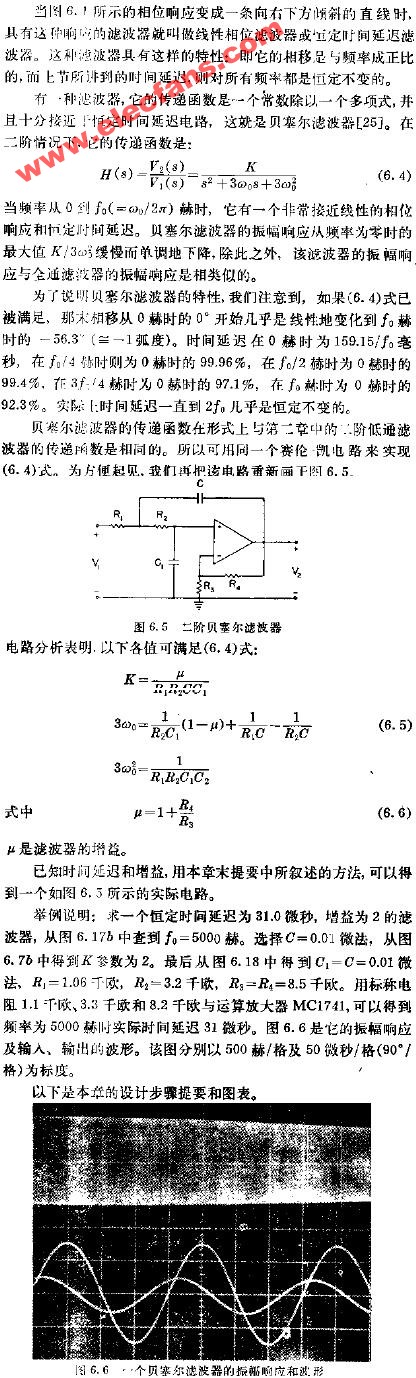
贝塞尔滤波器
贝塞尔滤波器又称最平时延或恒时延滤波器。其相移和频率成正比，即为一线性关系。但是由于它的幅频特性欠佳，而往往限制了它的应用。
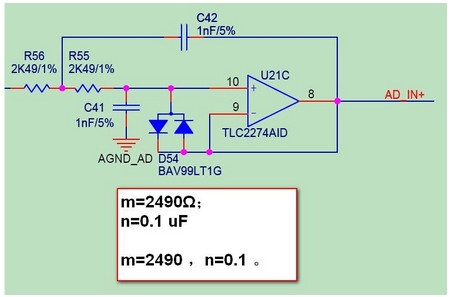
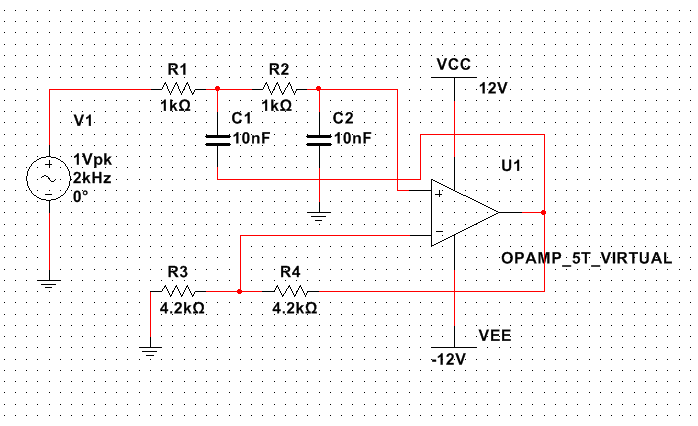
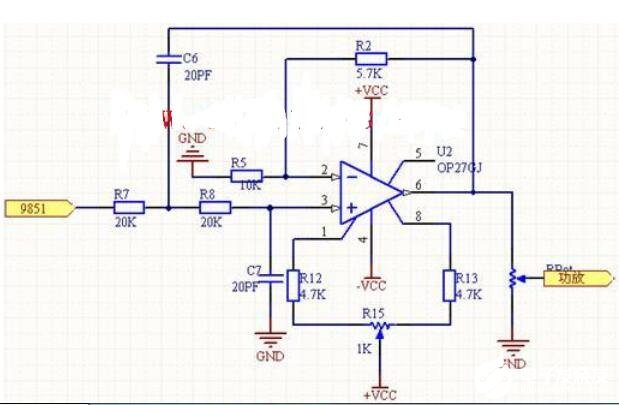
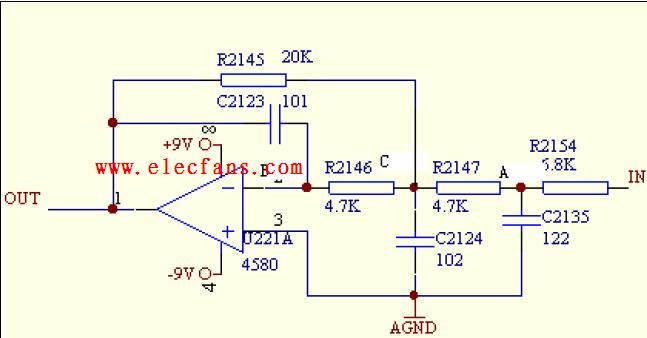
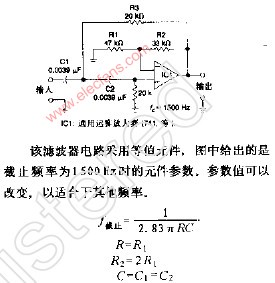
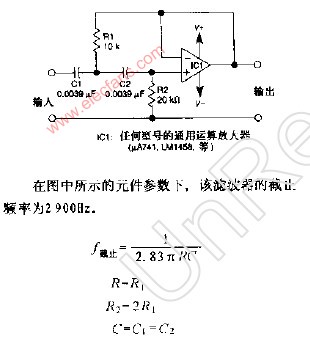
巴特沃兹低通滤波中用的最多的是赛伦凯乐电路，即仿真的该电路。
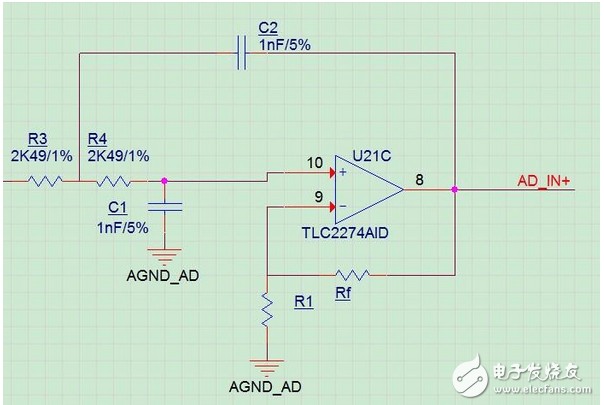
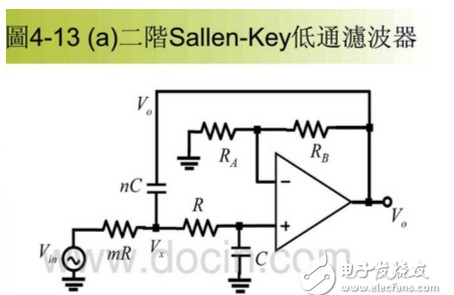
当两级RC电路的电阻、电容值相等时，叫赛伦凯电路，在二阶有源电路中引入一个负反馈，目的是使输出电压在高频率段迅速下降。
二阶有源低通滤波电路的通带放大倍数为 1+Rf/R1 ，与一阶低通滤波电路相同。
工商网监
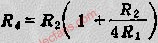
评论