1、特性阻抗
在直流或低频时,各器件或各设备之间互相连接时,随意拉两根线就行了。当频率高到长度与波长可比时,就要用同轴线或双绞线连接了。而且连接时要采用连接器,否则会造成失配甚至乱辐射以致不能正常工作。传输线是用来传输的,要不辐射,最简单的方法就是加个屏蔽套,做成屏蔽线。尺寸均匀,做成同轴状的传输线称为同轴线,内充介质便于弯曲的同轴线称为同轴电缆或射频电缆。
电波在同轴线内传输时,必须尺寸均匀才能顺畅,否则会产生反射。因此同轴线互连
时有个规格或参数问题,必须参数相同才行;这个参数就是特性阻抗ZC,有时也写成Z0.
习惯上Z0表示50Ω,而ZC泛指特性阻抗。无穷长的同轴线缆肯定是没有反射的,这时他的输入阻抗称为特性阻抗。
一段线输出端接上一个负载,假如输入端没有反射的话,这个负载的阻抗就是这段线的特性阻抗。特性阻抗是一个由尺寸与介质决定的电参数,同轴线的特性阻抗公式为:
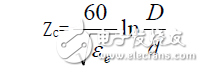
(式中εe为同轴线内充填介质的有效介电常数,D 为外导体内径,d 为内导体外径。)
2、反射系数、回损、驻波比
一段线接上输入阻抗为特性阻抗的负载是没有反射的,这种负载称为终端负载或精密负载。以它为参考,通常认为它的反射为零。假如一段线接上其它不匹配的负载ZL,必然有反射。这个反射必然正比于两者的差异,这就出现了反射系数Г这样一个参数。
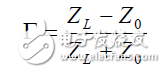
反射系数它是反映负载特性的最原始的参数,要想反射系数小一些,只要负载ZL接近特性阻抗Z0即可。虽然Г是个最原始的参数,也是测量出的参数,但由于是复数,一般人并不习惯用它。习惯上描述不匹配的程度常用回损RL,或驻波比SWR。
返回损失(回损)= 20logΓdB ,由于Γ≤1,一般为负值,但习惯上不讲负号。
驻波比,这是一个天馈线中最常见的一个技术指标,英文缩写为S.W.R,也有用V.S.W.R,即强调是电压之比。
线上电压因反射的存在而出现有高有低的现象并不是我们希望的,我们希望|Г|→0,也就是ρ→1。
3、史密斯圆图
为了便于形象化的理解阻抗情况与匹配的过程,作些简单的计算时,采用圆图就非常方便了。
1)反射系数同心圆(等|Г|圆或等ρ圆)
对于某一传输线端接任一负载的情况下,可用它的Г值来表示,不管你的负载为何值,它必然落在|Г|=1的圆内。
让我们画一个半径为1的圆,则圆心代表反射为零的点,过零点画一根水平线,左右两交点分别代表Г= -1(即∠180°)与Г=1,则任意一段传输线上的任一点,都可以在圆内找到其对应的|Г|∠ф。将直径等分即得如下图所示的等反射圆。
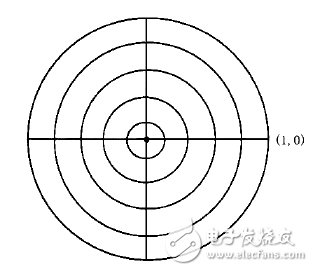
(等|Г|圆或等ρ圆)
在一根传输线上移动时,其|Г|值是不变的,只是相位随距离而变,正好在等|Г
圆上转。看这个图时请注意,相位为-2lβ,即l越长,相位越落后,因此图上l的方向是顺时针方向。另外还有一个2倍,即转角快了一倍;如l=λ/2,在圆上就转了360°,仍在原地。
此图一般是用等驻波比画的,不如等|Γ|均匀等距好画。半径表示|Г|(或ρ),越靠近圆心反射越小。假如将半径分成十等分, 画上十个同心圆,则圆图类似于打靶用的靶。
2)等阻圆与等抗圆
圆图的制作上有这样一个要求,那就是要用归一化阻抗,即z=Z/Z0,对于50Ω的同轴线,50Ω负载的归一化阻抗为1。用小写字母表示归一值:由下式可以简化得到等阻圆和等抗圆。
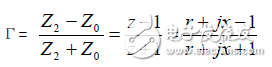
等阻圆为一偏心圆族,圆心在,半径为。
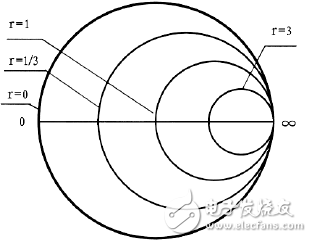
(等阻圆)
等抗圆圆心在,半径为的圆族,上面为正,下面为负。
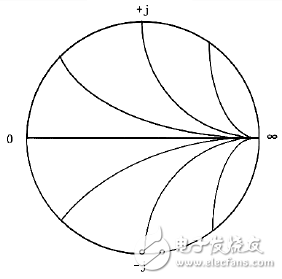
(等抗圆)
3)阻抗圆图
将三种圆画在一起就成了史密斯圆图,也常称阻抗圆图,或简作圆图。通常它是用来表示传输线上的输入阻抗的,水平轴为实数轴,上半面偏电感,下半面偏电容,右面(严格讲来是在r=1的圆内)阻值偏高,左面(在r=1的圆外)阻值偏低,因此将负载频响特性画在圆图上那情况将是一目了然的,该采取什么措施,也是一清二楚的。
阻抗圆图上适于作串联运算,若要作并联运算时,就要转成导纳,在圆图上这非常容易,某一点的反对称点即其导纳。
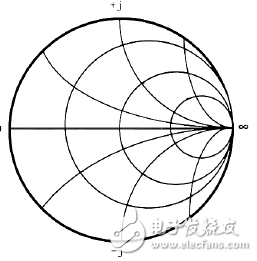
(史密斯圆图)
作阻抗运算时图上即阻抗,当要找某点的导纳值时,可由该点的矢径转180°即得;此时圆图所示值即全部成导纳。
另外注意一点,不管它是负载端还是源端,只要我们向里面看,它就是负载端,永远按离开负载方向为正转圆图,不要用源端作参考。
有人说圆图是微波技术上的一个重大发明,的确,史密斯将R+jX会出现的四个∞(+jx,-jx,r,|Z|)缩为圆上的一个点;而且极坐标上相位是连续的,比用直角坐标好;Γ为线性的同心圆坐标,形象的描述了传输线上的输入阻抗轨迹。在圆图上阻抗与导纳是兼容的。圆图作为输入阻抗特性的表征,用作简单的单节匹配计算是非常有用的,非常直观,把复杂的运算用简单的形象表现出来,概念清楚。
注:当在圆图上用归一化阻抗表示时(这是规定),某点的输入阻抗在经过λ/4后即成为该点的导纳.这是因为经λ/4线后的Z2变成Z1,而Z1Z2=Z02,在用归一化表达后z1z2=1,所以z1= 1/z2 = y2 。
4.参考面概念
要建立一个概念,那就是传输线上每点的输入阻抗都是不同的。也就是说输入阻抗是位置坐标的函数,同时也是频率的函数;只有Z2=Z0这一点除外,而这一点通常是作不到的.因此谈输入阻抗时必须说明是哪一点的 ,或者说参考面设在何处。
如一条线上只有一个产生反射的点,或者说产生最大反射的点,则参考面应当取在该点,这样该采取什么措施就一目了然了.假如参考面差得太远,此时各测试点连成的轨迹呈盘香状.这时就得考虑移参(仪器上的移动参考面功能,简作移参)了。
输入阻抗(或导纳)在圆图上是变的,它的轨迹就是等|Г| 或等驻波比圆;也就是说,无耗传输线反射系数的幅值是不变的,或者说驻波比是不变的,只是相位在变;因此通常用驻波比ρ来对天馈线提要求,是很自然的。因为这样做既简单又明了,比对输入阻抗提要求方便多了。但是若要进行阻抗匹配工作,就得用输入阻抗了,否则就太盲目了。
用圆图来表示反射的性质,或描绘整个匹配过程,那是最明确不过的了。而且用作匹配时,该采取什么措施也可说是一目了然的。另外圆图还可用来做简单计算。
5.相位量φ简单介绍
相位是一个时间上的量,它是描述正弦信号的一个参量。式中ω为角频率(实质为角速率),φ0为初相。
V=Vmsinφ=Vmsin(ωt+φ0)=Vmsin(2πft+φ0)
当线上为纯行波时,由于波行进需要时间,就会产生相位延迟(时)t = x/c,由t造成的相移φ为:ωt=ωx/c=ωx/λf=2πfx/λf=2πx/λ=βx ,这就得到了相移系数β,即一段线x所产生的相移为βx,将时间上的相移与空间上的相移相加,可得φ=ωt±βx+φ0 因此线上(一维)波的瞬时值表达式为:V=Vmsin(ωt±βx+φ0)
±号决定于波行进的方向。Φ虽然与空间有关,但它仍然是个时间变量。讨论问题时,总是假定t不变(或t=0)来讨论x的影响,或者x不变来讨论t的影响。而在某一点上来看,即x不变,而ωt又相同,也就只与φ0有关了,这就使得两信号之间的处理变成了平面上的矢量运算,而能测相位的网络分析仪也就称为矢量网络分析仪了,
一般情况下,传输线上既有入射波,也有反射波,它们分别满足相移与距离的正比关系,而一段线缆的相移却并不一定满足相移与长度的正比关系,除非上面没有反射波。
-
负载
+关注
关注
2文章
564浏览量
34325 -
阻抗
+关注
关注
17文章
957浏览量
45912
发布评论请先 登录
相关推荐
阻抗匹配与史密斯(Smith)圆图:基本原理
阻抗匹配与史密斯圆图
怎样理解阻抗匹配_pcb阻抗匹配如何计算

史密斯圆图的的天线阻抗匹配解决方案





 采用圆图理解阻抗匹配
采用圆图理解阻抗匹配











评论