引言
神经网络中涉及到大量的张量运算,比如卷积,矩阵乘法,向量点乘,求和等。神经网络加速器就是针对张量运算来设计的。一个神经网络加速器通常都包含一个张量计算阵列,以及数据收发控制,共同来完成诸如矩阵乘法,卷积等计算任务。运算灵活多变的特性和硬件的固定架构产生了矛盾,这个矛盾造成了利用硬件执行计算任务的算法多变性。不同的硬件架构实现相同的计算,可能具有不同的算法。我们今天讨论基于脉动阵列的计算架构,脉动阵列的低延迟,低扇出特性使其得到广泛应用,比如TPU中。我们今天就从矩阵计算讲起,谈一谈矩阵计算的几种不同方式,矩阵的一些特性,再讲一讲CNN中的卷积运算,最后谈谈这些张量计算在硬件中的实现形式。
矩阵计算
假设有两个矩阵:
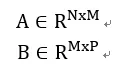
计算这两个矩阵的乘积
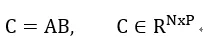
根据矩阵计算形式,我们可以看出有三级循环。根据排列组合,可以有6种计算形式。我们使用ijk分别表示A对应的行,列(B的行),以及B的列的标号。这六种循环计算方式为:ijk, jik, ikj, jki, kij, kji。这六种方式在硬件上(脉动阵列)实现起来,考虑到缓存和计算结构,实际上可以分为2种方式。
1) 矩阵x向量
我们用伪代码表示为:
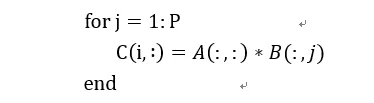
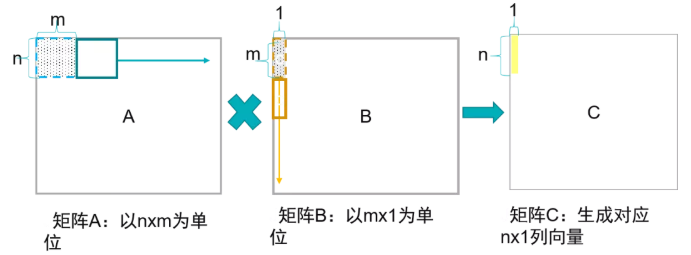
在这种方式下,通过矩阵x向量的方式可以配合脉动阵列的2D结构。这个时候片上要先存储下一个A矩阵和B矩阵的一列,然后通过一个周期完成矩阵x向量的计算,得到了C矩阵的一行。这个时候片上A矩阵数据可以一直保存不更换,而不断更换每一列的B数据,直到完成AB计算。
这种方式在在语音处理的LSTM等网络中比较适用,因为语音通常都是一些连续的向量,而且LSTM网络决定了连续的向量之间有依赖关系,因此矩阵x向量方式可以提高LSTM中权重的时间复用率。所谓时间复用率是指权重可以在片上保持较长的时间,而不断更换输入。从时间维度上看,权重得到了复用。
这种方式的缺点是权重加载到片上会消耗很多时间,突发的load需要占据很大访问内存带宽。而且对片上缓存要求容量较高。特别是当缓存较小权重数量较大的时候,就要通过不断加载权重到片上来满足计算需求,这可能会降低加速器性能。为了满足计算的实时性,权重输出带宽需要足够一个矩阵x向量的计算。这对片上带宽要求也较高。当然这些都能够通过一定手段来缓解,比如通过多batch来增加权重空间复用率,降低对带宽需求和片上缓存要求。
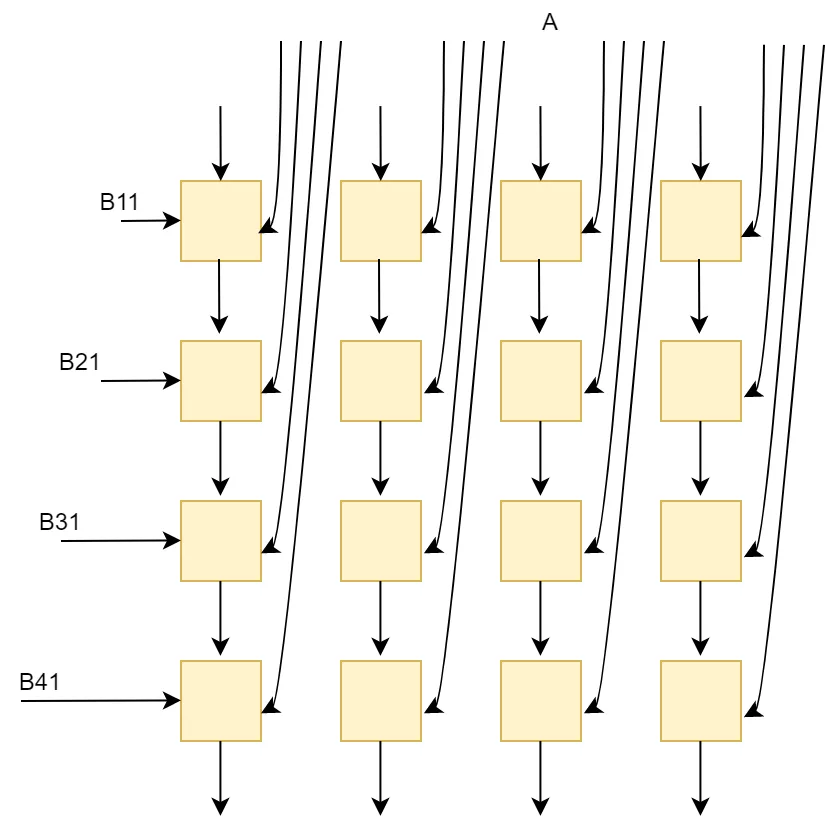
2) 列向量x行向量
用伪代码表示如下:
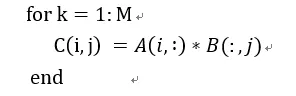
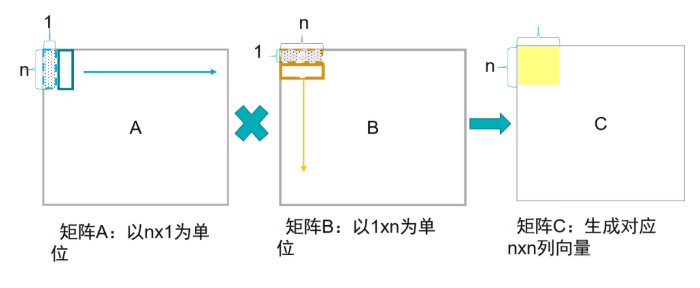
这实际上是取得A的一个列向量和B的行向量进行矩阵乘法,得到一个矩阵,所有对应的A的列和B的行乘积的矩阵和就是最终的C矩阵。这种方式利用了A和B的空间复用率,A的列和B的行的元素彼此求积,也适配了2D的脉动阵列结构。
这种方式对A和B的带宽需求最低,一般外部DDR的内存可以满足这样的要求。对片上缓存需求较低,带宽也较低。A的列元素和B的行元素分别从脉动阵列的左侧和上侧进入,相互乘积,达到了元素最大空间复用率。这种方式可能会要求对某个矩阵进行转置,比如当矩阵按行序列排的时候,B矩阵就需要经过转置后送入矩阵运算单元进行计算。
但是这种方式也有一定应用限制,对于矩阵x向量的语音识别来说,只有对于batch size较大时,效率才会高,否则会比较低。而且这种结构不太利于脉动阵列在其它方面的应用,比如卷积计算,接下来我们会讲到。
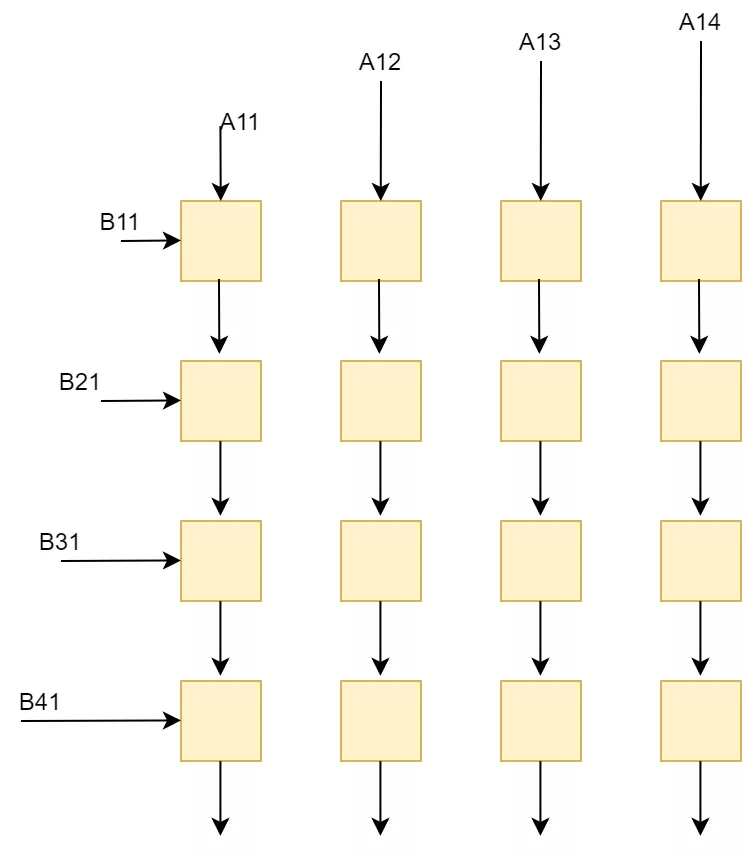
块矩阵计算
硬件上计算阵列通常都是和要进行计算的矩阵大小是不匹配的,一种情况就是计算阵列维度比矩阵维度小,一种就是大于矩阵的维度。
当小于矩阵维度时,可以通过对矩阵切块来分别计算,如果大于矩阵维度,可以对矩阵进行“补块”。比如硬件上计算阵列大小是32x32,而A矩阵是64x64,B矩阵是64x64。
如果采用列向量x行向量的方法,我们就可以将A和B分别切分成4个矩阵快,这些矩阵块分别进行计算。
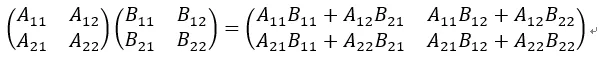
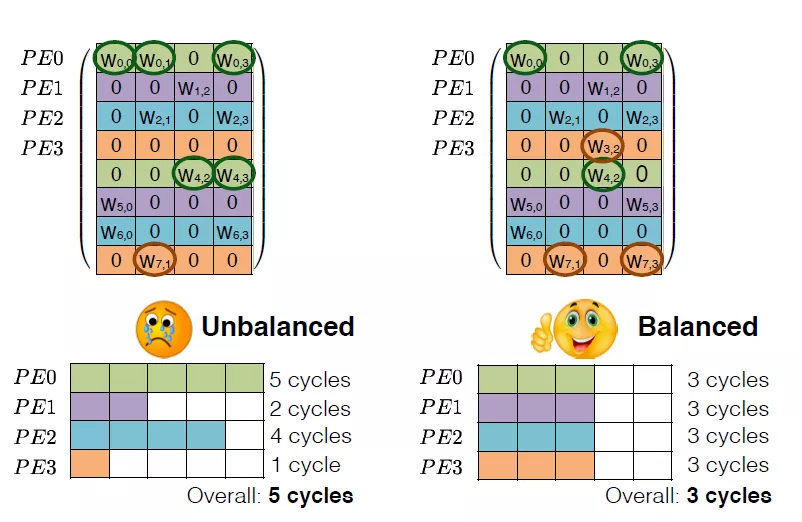
先计算A11xB11(分别将A11按列送入阵列,B11按行输入阵列,阵列中每个计算单元保留结果继续和下一次数据求累加和),然后计算A12xB21(继续不断将矩阵送入计算阵列,并和上次A11xB11结果求和),两者求和就得到了第一个矩阵块。
如果采用矩阵x向量的方法,就可以这样分块:

我们先在片上缓存下A1矩阵块,然后分别加载B1矩阵的列和A1进行矩阵向量计算,分别得到了A1B1矩阵的第一列,第二列,…结果。
矩阵数据表示宽度
硬件上进行神经网络加速都采用量化后的数据,一般将训练的模型定点到16bit,8bit,4bit等对硬件计算友好的宽度。因此具有宽bit计算单元的硬件架构可以兼容低bit的神经网络计算,但是这样会造成计算资源浪费。所以通常有两个办法:一种是针对不同位宽开发不同硬件架构,另外一种是开发出一种同时兼容多种bit的架构。FPGA可重配置的特点,可以在开发阶段考虑多种bit计算架构,通过使用参数化定义来为使用者提供架构的可配置选项,客户可以依据自己需求选择使用哪种功能。这种方式既满足了不同bit的计算需求,同时又能够最大化FPGA资源的使用。
如果我们在低bit架构的基础上,增加一些其它模块,也能够同时兼容宽bit计算任务。这利用到了数据的分解。比如两个矩阵A和B分别是8bit,我们要用4bit硬件架构加以实现。将A和B按照4bit进行分解:

这个时候看到存在移位和求和,因此硬件中除了4bit计算阵列外,还需要有移位模块,加法模块,以及数据位宽转换模块。

假设矩阵乘法模块输入位宽4bit,输出32bit可以满足一般的矩阵大小的乘法,这输出的32bit数据先通过片上bus缓存到buffer或者给到shift+add模块,shift+add模块进行移位求和操作,得到的结果就是正常一个8bit矩阵乘法的结果,这个结果通常在神经网络中还会被进一步量化,我们假设量化到16bit,那么输出结果就存放到buffer中。在设计片上buffer的时候,数据单位如果是固定的会使得逻辑简单,但是现在存在4种数据位宽,所以对buffer中数据的使用就要能灵活处理4bit,8bit,16bit,32bit这样的大小。这些无疑增加了bufer复杂度。而且shift+add的结构也会增加大量的加法和移位逻辑。
矩阵压缩
神经网络种含有的参数很多,大的话都在几十M甚至上百M。为了在FPGA上能容纳更多参数,加速计算任务。通常有两种方式来对权重进行压缩:一种是对神经网络种冗余权重进行剪枝,另外一种是在FPGA上实现对参数压缩存储。
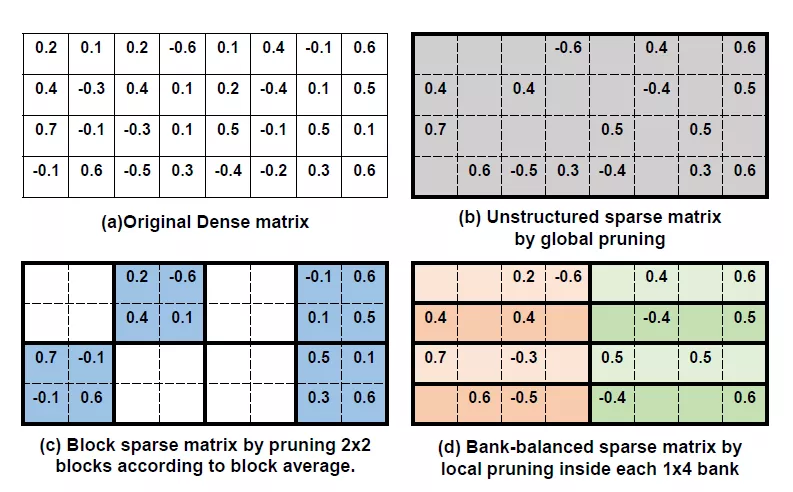
剪枝算法有很多,比如针对LSTM的有权重矩阵的稀疏化,设定阈值,去除阈值以下的数据,然后进行fine-tune。这样得到的矩阵是稀疏矩阵。可以大大减少权重数量。但是这样的矩阵结构不太利于硬件进行加速,因为它的结构不够整齐。
为了得到利于硬件部署的矩阵压缩结构,可以对权重进行结构化剪枝,即去除一整行或者一整列的数据,保持权重整齐的结构,有利于硬件上进行加速。
Huffman编码是一种简洁无损压缩的熵编码,简单来讲就是通过统计输入数据的分布概率,然后重新使用字符来表达原始数据。用最少bit的字符来描述出现概率最大的原始数据,这样就可以得到一个最优的压缩比率。编码可以提前进行,FPGA部分主要是完成解码。Huffman编码的压缩率对于矩阵数据压缩率很高,唯一的问题是解码逻辑比较大,解码效率比较低。这也是很少使用的原因。
卷积
CNN网络用大量的卷积运算来不断提取图像特征,使用了LSTM网络的语音识别中也有很多包含了卷积处理。CNN中大部分是2D卷积运算,语音识别中很多是1D卷积。通常在每一层卷积神经网络中含有多个输入通道和输出通道,本层输出通道就是下层的输入通道。每层的输入通道都有一个卷积核,这些输入通道会在卷积之后求和,得到一个输出通道的结果。
当我们采用脉动阵列来实现卷积的时候,可以有以下几种方式:
1) 卷积运算->稀疏矩阵乘法
我们以一个1D卷积举例,假设有个卷积核大小为3x1,输入向量长度为32。这个卷积用伪代码表示为:
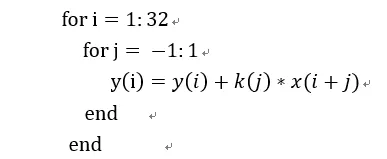
我们将卷积核扩展为一个稀疏矩阵,就可以表达为矩阵向量:

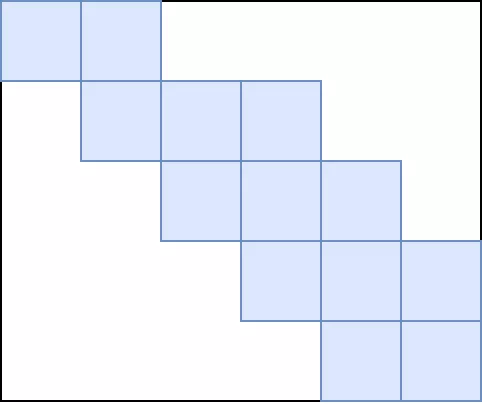
这个卷积矩阵用图像更清楚:蓝色是有效数据,白色是0。用这种方式很简单的就可以在脉动阵列上进行计算,只需要预先将卷积转化为矩阵。但是这样做的缺点就是需要浪费很多存储空间,同时对计算单元的利用率很低,除非卷积核维度比较大,否则如上卷积核和向量的维度比率,利用率只有3/32。
2) 利用输入输出通道,将卷积转化为矩阵乘法和求和。
我们假设1D卷积核为k,输入输出通道分别为i和o。则卷积核表示为:K(o,i)
还假设它是3x1大小。输入向量是x,假设它长度是32,则某个输入通道的向量就是:x(i)
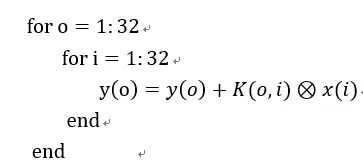
我们看出这个是不是特别像矩阵x向量。如果我们把卷积核分解为三组矩阵,每个矩阵由卷积核对应某个元素在i和o方向拓展得到,那么这样一个卷积运算就可以被我们转化为矩阵x向量+矩阵x向量。假设这三组卷积核矩阵是K1(o,i),K2(o,i)和K3(o,i)。同时x按照每个通道的对应元素展开成一个输入通道i的向量,X1(i), X2(i), …X32(i)。那么我们就可以算出输出结果是(用第一个y的结果举例):
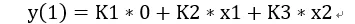
3) 利用脉动阵列结构,改动控制逻辑,直接进行卷积计算。
这个时候需要修改控制逻辑,让矩阵乘法阵列可以进行卷积计算。其实还可以在i和o的方向将之看作矩阵,但是每个计算单元还存在内部循环读取卷积核数据。

总结
以上分别总结了矩阵乘法,卷积运算在FPGA加速器上的实现方式。设计一款神经网络加速器是很多部门的通力合作,算法FPGA编译器架构,往往一个方案对于某个部门简单,但是令另外一个部门痛苦。大家在不断的“拉锯扯皮”中,一个方案就出来了。
-
FPGA
+关注
关注
1629文章
21729浏览量
602957 -
加速器
+关注
关注
2文章
796浏览量
37838 -
神经网络
+关注
关注
42文章
4771浏览量
100708 -
张量
+关注
关注
0文章
7浏览量
2562
发布评论请先 登录
相关推荐




 张量计算在神经网络加速器中的实现形式
张量计算在神经网络加速器中的实现形式










评论