贝叶斯优化是机器学习超参数优化的常用技术之一,本文不会使用艰深的数学论证,而是通过简单的术语带你领略贝叶斯优化之美。
假设有一个函数 f(x)。其计算成本很高,它不一定是分析表达式,而且你不知道它的导数。
你的任务:找到全局最小值。
当然,这是一个困难的任务,而且难度超过机器学习领域内的其它优化问题。梯度下降就是一种解决方案,它能通过函数的导数,利用数学捷径来实现更快的表达式评估。
或者,在某些优化场景中,函数的评估成本较低。如果你能在几秒内得到输入 x 的变体的数百种结果,那么使用简单的网格搜索就能得到很好的结果。
或者,你还可以使用一整套非常规的非梯度优化方法,比如粒子群或vwin 退火。
不幸的是,当前的任务没有这样的便利。我们的优化受到了多个方面的限制,其中最显著的包括:
计算成本高。理想情况下,只要我们查询函数的次数足够多,我们就能在实质上将它复现出来,但在实际情况下,输入的采样很有限,优化方法必须在这种情况下也能有效工作。
导数未知。在深度学习以及其它一些机器学习算法中,梯度下降及其变体方法依然是最常用的方法,这当然是有原因的。知道了导数,能让优化器获得一定的方向感——我们没有这种方向感。
我们需要找到全局最小值,这个任务即使对于梯度下降这种复杂精细的方法来说也很困难。我们的模型有时需要某种机制来避免被困于局部最小值。
解决方案:针对以最少的步骤寻找全局最小值的问题,贝叶斯优化是一个优雅的框架。
我们来构建一个假设的示例函数 c(x),即一个模型在给定输入 x 下的成本。当然,这个函数的实际情况对优化器来说是未知的。假设 c(x) 的实际形状如下:这就是所谓的「目标函数」。
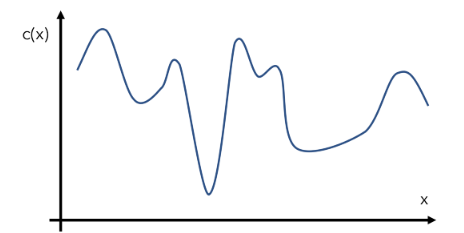
贝叶斯优化可通过一种名为「代理优化(surrogate optimization)」的方法解决这一问题。在语境中,代理母亲(代孕妈妈)是指同意为其他人生小孩的女人。基于同样的语境,代理函数是指目标函数的一种近似。
代理函数可基于采样得到的数据点而构建。
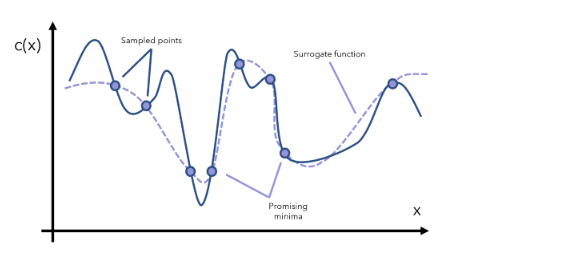
我们可以根据代理函数来识别哪些点是有潜力的最小值。然后我们在这些有潜力的区域执行更多采样,然后据此更新代理函数。
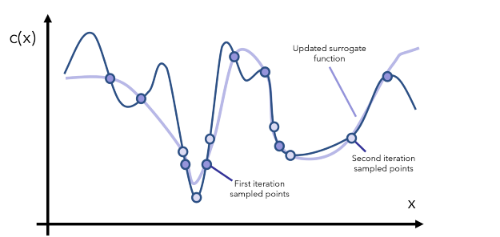
在每一次迭代中,我们都要继续观察当前的代理函数,通过采样对相关区域有更多了解,然后更新函数。注意,代理函数可表示成评估成本低得多的数学形式(比如用 y=x 近似表示一个成本更高的函数 y=arcsin((1-cos²x)/sin x) 的某个特定范围)。
经过一定数量的迭代之后,我们的目标是抵达全局最小值,除非该函数的形状非常古怪(比如其中有大量大起大落的部分),这时候你就要问自己了:是不是数据有问题?
我们先来欣赏一下这种方法的美妙之处。它不会对函数做出任何假设(只要它是可优化的既可)、不需要导数的相关信息、可通过巧妙地使用不断更新的近似函数来执行常识推理。对原本的目标函数的高成本估计也不再是问题。
这是一种基于代理的优化方法。但它的贝叶斯性质体现在哪里?
贝叶斯统计和建模和本质是基于新信息先验(之前的)信念,然后得到更新后的后验(之后的)信念。这里的代理优化就是这样工作的,使得其能通过贝叶斯系统、公式和思想很好地表示。
我们来更仔细地看看这个代理函数,其通常表示成高斯过程,这可被看作是一种掷骰子过程,返回的是与给定数据点拟合的函数(比如 sin 或 log),而不是数字 1 到 6. 这个过程会返回若干函数以及它们各自的概率。
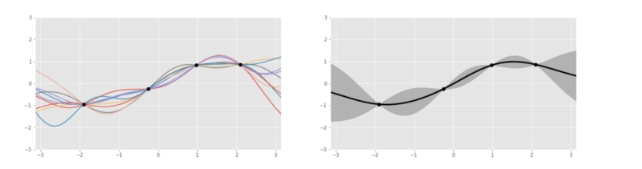
左图:基于 4 个数据点生成的几个基于高斯过程的函数;右图:将这些函数聚合之后。
Oscar Knagg 这篇文章直观地介绍了高斯过程的工作方式:https://towardsdatascience.com/an-intuitive-guide-to-gaussian-processes-ec2f0b45c71d
为什么要使用高斯过程来建模代理函数,而不是使用其它曲线拟合方法?这是因为高斯过程本质上就是贝叶斯模式的。高斯过程是一种概率分布,就像一个事件的最终结果分布一样(比如掷硬币的 1/2 概率),只不过高斯过程是在所有可能的函数上的分布。
举个例子,我们也许可以定义当前的数据点集可由函数 a(x) 表示 40%、由函数 b(x) 表示 10% 等等。通过将代理函数表示成概率分布,可使用新信息,通过固有的概率贝叶斯过程来完成更新。也许当新信息被引入时,a(x) 函数又只能表示 20% 的数据了。这样的变化受贝叶斯公式的约束。
这会使得类似于新数据点的多项式回归拟合这样的目标难以完成甚至不可能完成。
表示成先验概率分布的代理函数会通过一个「获取函数(acquisition function)」而更新。这个函数负责在探索与利用权衡的基础上,对提议的新点进行测试。
利用的目标是采样代理模型能很好地预测目标函数的地方。这会用到已知的有潜力的位置。但是,如果我们已经充分探索了某个特定的区域,再继续利用已知信息也收益不大了。
探索的目标是采样不确定度较高的位置。这能确保空间中不留下未探索的主要区域——全局最小值可能就藏在此处。
太过重视利用而不太重视探索的获取函数会让模型驻留于其发现的第一个最小值(通常是局部最小值)。反过来,重探索而轻利用的获取函数则一开始就不会留在某个最小值,不管是局部最小值还是全局最小值。因此,为了得到很好的结果,需要达到微妙精巧的平衡。
获取函数 a(x) 必须兼顾探索和利用。常见的获取函数包括预期提升和提升的最大可能性,所有这些衡量的都是给定有关先验(高斯过程)的信息下,一个特定输入在未来产生回报的概率。
我们归总一下这些知识点。贝叶斯优化的执行方式为:
初始化一个高斯过程「代理函数」先验分布。
选择几个数据点 x 使得获取函数 a(x) 在当前先验分布上的结果是最大的。
在目标成本函数 c(x) 中评估数据点 x 并获取其结果 y。
使用新数据更新高斯过程先验分布,得到一个后验分布(这将作为下一步的先验分布)。
重复第 2-5 步并多次迭代。
解读当前的高斯过程分布(成本很低),找到全局最小值。
贝叶斯优化的核心是将概率思想融入到代理优化思想之中。这两种思想组合到一起,能创造出一种强大的系统。该系统具有很多应用场景,从医药产品开发到自动驾驶汽车。
不过,贝叶斯优化最常见的应用领域还是机器学习,尤其是超参数优化任务。举个例子,如果我们要训练一个梯度上升分类器,则会遇到几十个超参数,从学习率到最大深度再到最小不纯度拆分值。在这里,x 表示模型的超参数,c(x) 表示模型在给定超参数 x 下的表现。
使用贝叶斯优化的主要动机是:在有些场景中,评估输出的成本非常高。首先,需要使用这些参数构建一整个集成树;其次,它们需要运行并完成几次预测,这对于集成方法来说成本高昂。
可以这样说,在给定一组参数的条件下,使用神经网络来评估损失函数的速度更快:只是重复执行矩阵乘法,这是非常快的,尤其是使用专用计算硬件时。这是使用梯度下降的原因之一,也就是反复查询以找到前进的方向。
总结
代理优化是使用一个代理函数或近似函数来通过采样估计目标函数。
贝叶斯优化是通过将代理函数表示成概率分布而将代理优化放入一个概率框架中,然后再使用新信息更新这个分布。
获取函数则是用于基于已知的先验,评估利用空间中的某个特定点得到「好」结果的概率。其关键在于探索与利用的平衡。
贝叶斯优化的主要使用场景是目标函数评估成本高的任务,比如超参数调节。有一些用于该任务的软件库,比如 HyperOpt。
编辑:hfy
-
函数
+关注
关注
3文章
4327浏览量
62567 -
贝叶斯
+关注
关注
0文章
77浏览量
12564 -
机器学习
+关注
关注
66文章
8406浏览量
132555
发布评论请先 登录
相关推荐
使用PyMC3包实现贝叶斯线性回归
机器学习之朴素贝叶斯应用教程

如何理解贝叶斯公式
机器学习之朴素贝叶斯
带你入门常见的机器学习分类算法——逻辑回归、朴素贝叶斯、KNN、SVM、决策树
一文秒懂贝叶斯优化/Bayesian Optimization





 机器学习:简单的术语带你领略贝叶斯优化之美
机器学习:简单的术语带你领略贝叶斯优化之美












评论