在强化学习(五)用时序差分法(TD)求解中,我们讨论了用时序差分来求解强化学习预测问题的方法,但是对控制算法的求解过程没有深入,本文我们就对时序差分的在线控制算法SARSA做详细的讨论。
SARSA这一篇对应Sutton书的第六章部分和UCL强化学习课程的第五讲部分。
1.SARSA算法的引入
SARSA算法是一种使用时序差分求解强化学习控制问题的方法,回顾下此时我们的控制问题可以表示为:给定强化学习的5个要素:状态集SS, 动作集AA, 即时奖励RR,衰减因子γγ, 探索率ϵϵ, 求解最优的动作价值函数q∗q∗和最优策略π∗π∗。
这一类强化学习的问题求解不需要环境的状态转化模型,是不基于模型的强化学习问题求解方法。对于它的控制问题求解,和蒙特卡罗法类似,都是价值迭代,即通过价值函数的更新,来更新当前的策略,再通过新的策略,来产生新的状态和即时奖励,进而更新价值函数。一直进行下去,直到价值函数和策略都收敛。
再回顾下时序差分法的控制问题,可以分为两类,一类是在线控制,即一直使用一个策略来更新价值函数和选择新的动作。而另一类是离线控制,会使用两个控制策略,一个策略用于选择新的动作,另一个策略用于更新价值函数。
我们的SARSA算法,属于在线控制这一类,即一直使用一个策略来更新价值函数和选择新的动作,而这个策略是ϵ−ϵ−贪婪法,在强化学习(四)用蒙特卡罗法(MC)求解中,我们对于ϵ−ϵ−贪婪法有详细讲解,即通过设置一个较小的ϵϵ值,使用1−ϵ1−ϵ的概率贪婪地选择目前认为是最大行为价值的行为,而用ϵϵ的概率随机的从所有m个可选行为中选择行为。用公式可以表示为:
π(a|s)={ϵ/m+1−ϵϵ/mifa∗=argmaxa∈AQ(s,a)elseπ(a|s)={ϵ/m+1−ϵifa∗=argmaxa∈AQ(s,a)ϵ/melse
2. SARSA算法概述
作为SARSA算法的名字本身来说,它实际上是由S,A,R,S,A几个字母组成的。而S,A,R分别代表状态(State),动作(Action),奖励(Reward),这也是我们前面一直在使用的符号。这个流程体现在下图:
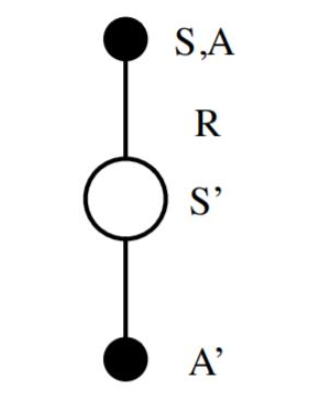
在迭代的时候,我们首先基于ϵ−ϵ−贪婪法在当前状态SS选择一个动作AA,这样系统会转到一个新的状态S′S′, 同时给我们一个即时奖励RR, 在新的状态S′S′,我们会基于ϵ−ϵ−贪婪法在状态S‘′S‘′选择一个动作A′A′,但是注意这时候我们并不执行这个动作A′A′,只是用来更新的我们的价值函数,价值函数的更新公式是:
Q(S,A)=Q(S,A)+α(R+γQ(S′,A′)−Q(S,A))Q(S,A)=Q(S,A)+α(R+γQ(S′,A′)−Q(S,A))
其中,γγ是衰减因子,αα是迭代步长。这里和蒙特卡罗法求解在线控制问题的迭代公式的区别主要是,收获GtGt的表达式不同,对于时序差分,收获GtGt的表达式是R+γQ(S′,A′)R+γQ(S′,A′)。这个价值函数更新的贝尔曼公式我们在强化学习(五)用时序差分法(TD)求解第2节有详细讲到。
除了收获GtGt的表达式不同,SARSA算法和蒙特卡罗在线控制算法基本类似。
3. SARSA算法流程
下面我们总结下SARSA算法的流程。
算法输入:迭代轮数TT,状态集SS, 动作集AA, 步长αα,衰减因子γγ, 探索率ϵϵ,
输出:所有的状态和动作对应的价值QQ
1. 随机初始化所有的状态和动作对应的价值QQ. 对于终止状态其QQ值初始化为0.
2. for i from 1 to T,进行迭代。
a) 初始化S为当前状态序列的第一个状态。设置AA为ϵ−ϵ−贪婪法在当前状态SS选择的动作。
b) 在状态SS执行当前动作AA,得到新状态S′S′和奖励RR
c) 用ϵ−ϵ−贪婪法在状态S′S′选择新的动作A′A′
d) 更新价值函数Q(S,A)Q(S,A):
Q(S,A)=Q(S,A)+α(R+γQ(S′,A′)−Q(S,A))Q(S,A)=Q(S,A)+α(R+γQ(S′,A′)−Q(S,A))
e)S=S′,A=A′S=S′,A=A′
f) 如果S′S′是终止状态,当前轮迭代完毕,否则转到步骤b)
这里有一个要注意的是,步长αα一般需要随着迭代的进行逐渐变小,这样才能保证动作价值函数QQ可以收敛。当QQ收敛时,我们的策略ϵ−ϵ−贪婪法也就收敛了。
4. SARSA算法实例:Windy GridWorld
下面我们用一个著名的实例Windy GridWorld来研究SARSA算法。
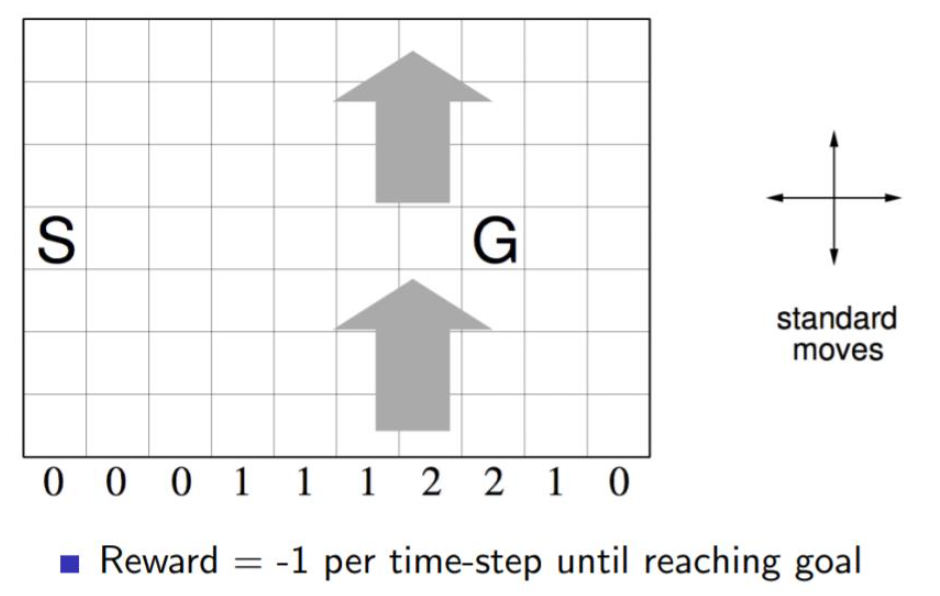
如下图一个10×7的长方形格子世界,标记有一个起始位置 S 和一个终止目标位置 G,格子下方的数字表示对应的列中一定强度的风。当个体进入该列的某个格子时,会按图中箭头所示的方向自动移动数字表示的格数,借此来vwin 世界中风的作用。同样格子世界是有边界的,个体任意时刻只能处在世界内部的一个格子中。个体并不清楚这个世界的构造以及有风,也就是说它不知道格子是长方形的,也不知道边界在哪里,也不知道自己在里面移动移步后下一个格子与之前格子的相对位置关系,当然它也不清楚起始位置、终止目标的具体位置。但是个体会记住曾经经过的格子,下次在进入这个格子时,它能准确的辨认出这个格子曾经什么时候来过。格子可以执行的行为是朝上、下、左、右移动一步,每移动一步只要不是进入目标位置都给予一个 -1 的惩罚,直至进入目标位置后获得奖励 0 同时永久停留在该位置。现在要求解的问题是个体应该遵循怎样的策略才能尽快的从起始位置到达目标位置。
逻辑并不复杂,完整的代码在我的github。这里我主要看一下关键部分的代码。
算法中第2步步骤a,初始化SS,使用ϵ−ϵ−贪婪法在当前状态SS选择的动作的过程:
# initialize state
state = START
# choose an action based on epsilon-greedy algorithm
if np.random.binomial(1, EPSILON) == 1:
action = np.random.choice(ACTIONS)
else:
values_ = q_value[state[0], state[1], :]
action = np.random.choice([action_ for action_, value_ in enumerate(values_) if value_ == np.max(values_)])
算法中第2步步骤b,在状态SS执行当前动作AA,得到新状态S′S′的过程,由于奖励不是终止就是-1,不需要单独计算:
def step(state, action):
i, j = state
if action == ACTION_UP:
return [max(i - 1 - WIND[j], 0), j]
elif action == ACTION_DOWN:
return [max(min(i + 1 - WIND[j], WORLD_HEIGHT - 1), 0), j]
elif action == ACTION_LEFT:
return [max(i - WIND[j], 0), max(j - 1, 0)]
elif action == ACTION_RIGHT:
return [max(i - WIND[j], 0), min(j + 1, WORLD_WIDTH - 1)]
else:
assert False
算法中第2步步骤c,用ϵ−ϵ−贪婪法在状态S‘S‘选择新的动作A′A′的过程:
next_state = step(state, action)
if np.random.binomial(1, EPSILON) == 1:
next_action = np.random.choice(ACTIONS)
else:
values_ = q_value[next_state[0], next_state[1], :]
next_action = np.random.choice([action_ for action_, value_ in enumerate(values_) if value_ == np.max(values_)])
算法中第2步步骤d,e,更新价值函数Q(S,A)Q(S,A)以及更新当前状态动作的过程:
# Sarsa update
q_value[state[0], state[1], action] += \
ALPHA * (REWARD + q_value[next_state[0], next_state[1], next_action] -
q_value[state[0], state[1], action])
state = next_state
action = next_action
代码很简单,相信大家对照算法,跑跑代码,可以很容易得到这个问题的最优解,进而搞清楚SARSA算法的整个流程。
5. SARSA(λλ)
在强化学习(五)用时序差分法(TD)求解中我们讲到了多步时序差分TD(λ)TD(λ)的价值函数迭代方法,那么同样的,对应的多步时序差分在线控制算法,就是我们的SARSA(λ)SARSA(λ)。
TD(λ)TD(λ)有前向和后向两种价值函数迭代方式,当然它们是等价的。在控制问题的求解时,基于反向认识的SARSA(λ)SARSA(λ)算法将可以有效地在线学习,数据学习完即可丢弃。因此SARSA(λ)SARSA(λ)算法默认都是基于反向来进行价值函数迭代。
在上一篇我们讲到了TD(λ)TD(λ)状态价值函数的反向迭代,即:
δt=Rt+1+γV(St+1)−V(St)δt=Rt+1+γV(St+1)−V(St)
V(St)=V(St)+αδtEt(S)V(St)=V(St)+αδtEt(S)
对应的动作价值函数的迭代公式可以找样写出,即:
δt=Rt+1+γQ(St+1,At+1)−Q(St,At)δt=Rt+1+γQ(St+1,At+1)−Q(St,At)
Q(St,At)=Q(St,At)+αδtEt(S,A)Q(St,At)=Q(St,At)+αδtEt(S,A)
除了状态价值函数Q(S,A)Q(S,A)的更新方式,多步参数λλ以及反向认识引入的效用迹E(S,A)E(S,A),其余算法思想和SARSA类似。这里我们总结下SARSA(λ)SARSA(λ)的算法流程。
算法输入:迭代轮数TT,状态集SS, 动作集AA, 步长αα,衰减因子γγ, 探索率ϵϵ,多步参数λλ
输出:所有的状态和动作对应的价值QQ
1. 随机初始化所有的状态和动作对应的价值QQ. 对于终止状态其QQ值初始化为0.
2. for i from 1 to T,进行迭代。
a) 初始化所有状态动作的效用迹EE为0,初始化S为当前状态序列的第一个状态。设置AA为ϵ−ϵ−贪婪法在当前状态SS选择的动作。
b) 在状态SS执行当前动作AA,得到新状态S′S′和奖励RR
c) 用ϵ−ϵ−贪婪法在状态S′S′选择新的动作A′A′
d) 更新效用迹函数E(S,A)E(S,A)和TD误差δδ:
E(S,A)=E(S,A)+1E(S,A)=E(S,A)+1
δ=Rt+1+γQ(St+1,At+1)−Q(St,At)δ=Rt+1+γQ(St+1,At+1)−Q(St,At)
e) 对当前序列所有出现的状态s和对应动作a, 更新价值函数Q(s,a)Q(s,a)和效用迹函数E(s,a)E(s,a):
Q(s,a)=Q(s,a)+αδE(s,a)Q(s,a)=Q(s,a)+αδE(s,a)
E(s,a)=γλE(s,a)E(s,a)=γλE(s,a)
f)S=S′,A=A′S=S′,A=A′
g) 如果S′S′是终止状态,当前轮迭代完毕,否则转到步骤b)
对于步长αα,和SARSA一样,一般也需要随着迭代的进行逐渐变小才能保证动作价值函数QQ收敛。
6. SARSA小结
SARSA算法和动态规划法比起来,不需要环境的状态转换模型,和蒙特卡罗法比起来,不需要完整的状态序列,因此比较灵活。在传统的强化学习方法中使用比较广泛。
但是SARSA算法也有一个传统强化学习方法共有的问题,就是无法求解太复杂的问题。在 SARSA 算法中,Q(S,A)Q(S,A)的值使用一张大表来存储的,如果我们的状态和动作都达到百万乃至千万级,需要在内存里保存的这张大表会超级大,甚至溢出,因此不是很适合解决规模很大的问题。当然,对于不是特别复杂的问题,使用SARSA还是很不错的一种强化学习问题求解方法。
-
算法
+关注
关注
23文章
4607浏览量
92819 -
控制算法
+关注
关注
4文章
166浏览量
21712 -
SARSA
+关注
关注
0文章
2浏览量
1318
发布评论请先 登录
相关推荐
对Rijndael的JAVA差分攻击与防范
SHACAL-2算法的差分故障攻击
修正的强跟踪有限差分滤波算法
基于差分隐私的轨迹模式挖掘算法

基于邻域差分和协方差信息处理单目标优化的进化算法
面向随机森林的差分隐私保护算法
浅谈Q-Learning和SARSA时序差分算法
强化学习的双权重最小二乘Sarsa算法





 浅谈时序差分的在线控制算法—SARSA
浅谈时序差分的在线控制算法—SARSA












评论