带你重新认识了一下真正的PID-德赢Vwin官网网

网上关于PID算法的文章很多，但是感觉有必要自己再进行一次总结，抽丝剥茧地重新认识了一下PID；

1 前言

2 开环控制

3 闭环控制

4 PID

4.1 系统架构

4.2 理论基础

4.3 离散化

4.4 伪算法

5 C++实现

6 总结

1 前言

控制系统通常根据有没有反馈会分为开环系统和闭环系统，在闭环系统的控制中，PID算法非常强大，其三个部分分别为；

P：比例环节；

I：积分环节；

D：微分环节；

PID算法可以自动对控制系统进行准确且迅速的校正，因此被广泛地应用于工业控制系统。

2 开环控制

首先来看开环控制系统，如下图所示，隆哥蒙着眼，需要走到虚线旗帜所表示的目标位置，由于缺少反馈（眼睛可以感知当前距离和位置，由于眼睛被蒙上没有反馈，所以这也是一个开环系统），最终隆哥会较大概率偏离预期的目标，可能会运行到途中实线旗帜所表示的位置。

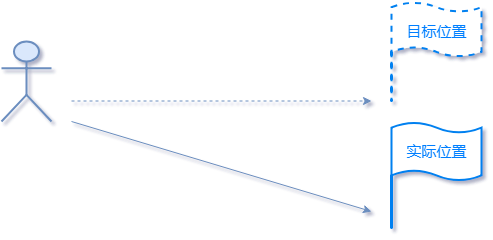
开环系统的整体结构如下所示；

这里做一个不是很恰当的比喻；

Input：告诉隆哥目标距离的直线位置（10米）；

Controller：隆哥大脑中计算出到达目标所需要走多少步；

Process：双腿作为执行机构，输出了相应的步数，但是最终仍然偏离了目标；

看来没有反馈的存在，很难准确到达目标位置。

3 闭环控制

所以为了准确到达目标位置，这里就需要引入反馈，具体如下图所示；

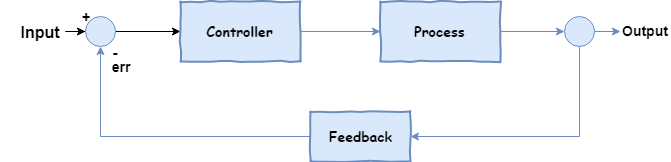
在这里继续举个不怎么恰当的比喻；隆哥重获光明之后，基本可以看到目标位置了；

第一步Input：告诉隆哥目标距离的直线位置（10米）；

第二步Controller：隆哥大脑中计算出到达目标所需要走多少步；

第三步Process：双腿作为执行机构，输出了相应的步数，但是最终仍然偏离了目标；

第四步Feedback：通过视觉获取到目前已经前进的距离，（比如前进了2米，那么还有8米的偏差）；

第五步err：根据偏差重新计算所需要的步数，然后重复上述四个步骤，最终隆哥达到最终的目标位置。

4 PID

4.1 系统架构

虽然在反馈系统下，隆哥最终到达目标位置，但是现在又来了新的任务，就是又快又准地到达目标位置。所以这里隆哥开始采用PID Controller，只要适当调整P，I和D的参数，就可以到达目标位置，具体如下图所示；

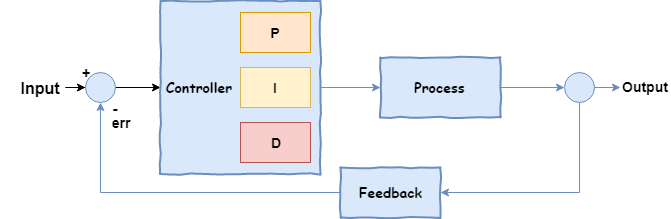
隆哥为了最短时间内到达目标位置，进行了不断的尝试，分别出现了以下几种情况；

跑得太快，最终导致冲过了目标位置还得往回跑；

跑得太慢，最终导致到达目标位置所用时间太长；

经过不断的尝试，终于找到了最佳的方式，其过程大概如下图所示；

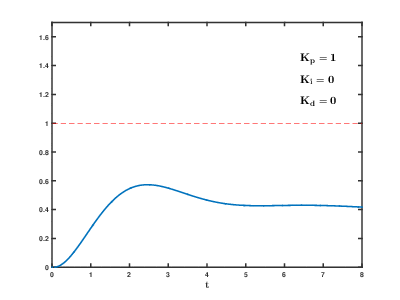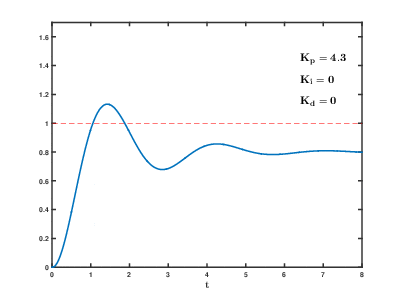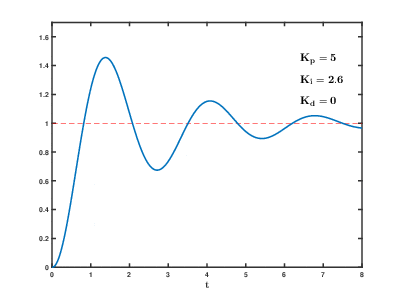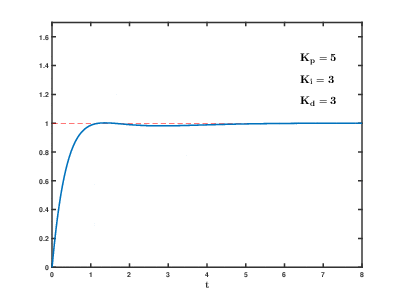
这里依然举一个不是很恰当的比喻；

第一步：得到与目标位置的距离偏差（比如最开始是10米，后面会逐渐变小）；

第二步：根据误差，预估需要多少速度，如何估算呢，看下面几步；

P比例则是给定一个速度的大致范围，满足下面这个公式；

因此比例作用相当于某一时刻的偏差（err）与比例系数的乘积，具体如下所示；

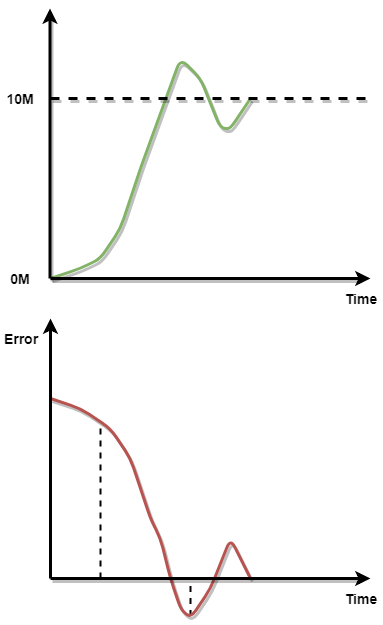
比例作用

绿色线为上述例子中从初始位置到目标位置的距离变化；红色线为上述例子中从初始位置到目标位置的偏差变化，两者为互补的关系；

I积分则是误差在一定时间内的和，满足以下公式；

如下图所示；

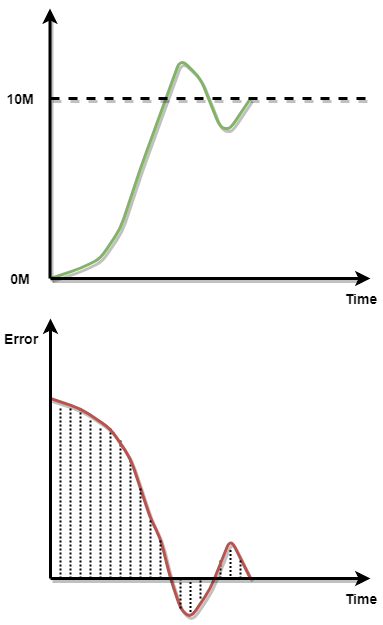
红色曲线阴影部分面积即为积分作用的结果，其不断累积的误差，最终乘以积分系数就得到了积分部分的输出；

D微分则是误差变化曲线某处的导数，或者说是某一点的斜率，因此这里需要引入微分；

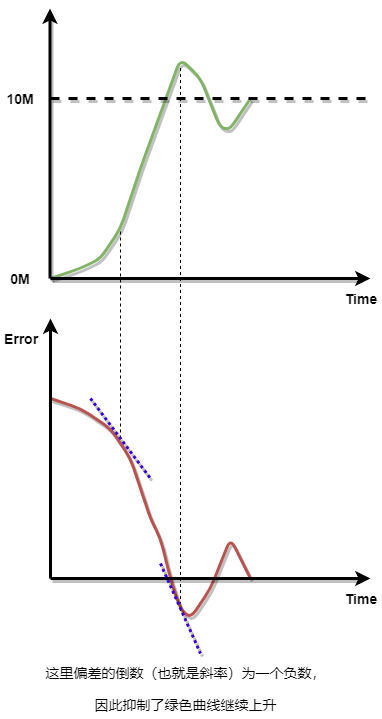
从图中可知，当偏差变化过快，微分环节会输出较大的负数，作为抑制输出继续上升，从而抑制过冲。

综上，，分别增加其中一项参数会对系统造成的影响总结如下表所示；

参数	上升时间	超调量	响应时间	稳态误差	稳定性
Kp	减少	增加	小变化	减少	降级
Ki	减少	增加	增加	消除	降级
Kd	微小的变化	减少	减少	理论上没有影响	小，稳定性会提升

4.2 理论基础

上面扯了这么多，无非是为了初步理解PID在负反馈系统中的调节作用，下面开始推导一下算法实现的具体过程；PID控制器的系统框图如下所示；

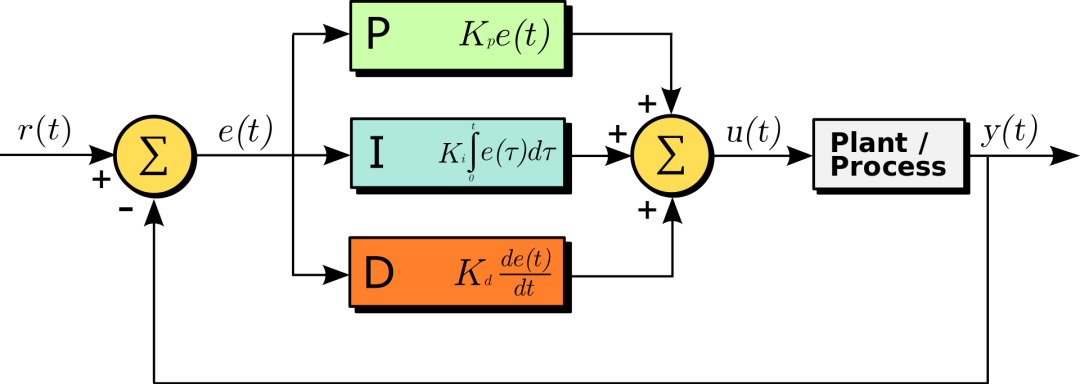
图片来自Wiki

因此不难得出输入和输出的关系；

是比例增益；是积分增益；是微分增益；

4.3 离散化

在数字系统中进行PID算法控制，需要对上述算法进行离散化；假设系统采样时间为则将输入序列化得到；

将输出序列化得到；

比例项：离散化

积分项：

微分项：

所以最终可以得到式①，也就是网上所说的位置式PID：

将式①再做一下简化；

最终得到增量式PID的离散公式如下：

4.4 伪算法

这里简单总结一下增量式PID实现的伪算法；

previous_error:=0//上一次偏差 integral:=0//积分和 //循环 //采样周期为dt loop: //setpoint设定值 //measured_value反馈值 error:=setpoint−measured_value//计算得到偏差 integral:=integral+error×dt//计算得到积分累加和 derivative:=(error−previous_error)/dt//计算得到微分 output:=Kp×error+Ki×integral+Kd×derivative//计算得到PID输出 previous_error:=error//保存当前偏差为下一次采样时所需要的历史偏差 wait(dt)//等待下一次采用 gotoloop

5 C++实现

这里是增量式PID算法的C语言实现；

pid.cpp

#ifndef_PID_SOURCE_ #define_PID_SOURCE_ #include #include #include"pid.h" usingnamespacestd; classPIDImpl { public: PIDImpl(doubledt,doublemax,doublemin,doubleKp,doubleKd,doubleKi); ~PIDImpl(); doublecalculate(doublesetpoint,doublepv); private: double_dt; double_max; double_min; double_Kp; double_Kd; double_Ki; double_pre_error; double_integral; }; PID::PID(doubledt,doublemax,doublemin,doubleKp,doubleKd,doubleKi) { pimpl=newPIDImpl(dt,max,min,Kp,Kd,Ki); } doublePID::calculate(doublesetpoint,doublepv) { returnpimpl->calculate(setpoint,pv); } PID::~PID() { deletepimpl; } /** *Implementation */ PIDImpl::PIDImpl(doubledt,doublemax,doublemin,doubleKp,doubleKd,doubleKi): _dt(dt), _max(max), _min(min), _Kp(Kp), _Kd(Kd), _Ki(Ki), _pre_error(0), _integral(0) { } doublePIDImpl::calculate(doublesetpoint,doublepv) { //Calculateerror doubleerror=setpoint-pv; //Proportionalterm doublePout=_Kp*error; //Integralterm _integral+=error*_dt; doubleIout=_Ki*_integral; //Derivativeterm doublederivative=(error-_pre_error)/_dt; doubleDout=_Kd*derivative; //Calculatetotaloutput doubleoutput=Pout+Iout+Dout; //Restricttomax/min if(output>_max) output=_max; elseif(output< _min ) output = _min; // Save error to previous error _pre_error = error; return output; } PIDImpl::~PIDImpl() { } #endif

pid.h

#ifndef_PID_H_ #define_PID_H_ classPIDImpl; classPID { public: //Kp-proportionalgain //Ki-Integralgain //Kd-derivativegain //dt-loopintervaltime //max-maximumvalueofmanipulatedvariable //min-minimumvalueofmanipulatedvariable PID(doubledt,doublemax,doublemin,doubleKp,doubleKd,doubleKi); //Returnsthemanipulatedvariablegivenasetpointandcurrentprocessvalue doublecalculate(doublesetpoint,doublepv); ~PID(); private: PIDImpl*pimpl; }; #endif

pid_example.cpp

#include"pid.h" #include intmain(){ PIDpid=PID(0.1,100,-100,0.1,0.01,0.5); doubleval=20; for(inti=0;i< 100; i++) { double inc = pid.calculate(0, val); printf("val:% 7.3f inc:% 7.3f ", val, inc); val += inc; } return 0; }

编译并测试；

g++-cpid.cpp-opid.o #Tocompileexamplecode: g++pid_example.cpppid.o-opid_example

6 总结

本文总结了PID控制器算法在闭环系统中根据偏差变化的具体调节作用，每个环节可能对系统输出造成什么样的变化，给出了位置式和增量式离散PID算法的推导过程，并给出了位置式算法的C++程序实现。

由于作者能力和水平有限，文中难免存在错误和纰漏，请不吝赐教。

责任编辑：YYX

声明：本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人，不代表德赢Vwin官网网立场。文章及其配图仅供工程师学习之用，如有内容侵权或者其他违规问题，请联系本站处理。举报投诉