在直流电路中,功耗仅是直流电压乘以直流电流(以瓦特为单位)的乘积。但是,对于带有无功分量的交流电路,我们必须以不同的方式计算消耗的功率。
电功率是电路中能量消耗的“速率”,因此,所有电气和电子组件及设备都对其可安全处理的电功率量有所限制。例如,一个1/4瓦的电阻器或一个20瓦的放大器,电力可能随直流量或交流量而随时间变化。电路在任何时刻的电量都称为瞬时电量,它由功率等于伏特乘以安培(P = V * I)的众所周知的关系给出。因此,一瓦特(每秒消耗一焦耳的能量的比率)将等于一伏特乘以一安培的伏安乘积。
那么,电路元件吸收或提供的功率就是该元件两端的电压V和流经该元件的电流I的乘积。因此,如果我们有一个电阻为“ R”欧姆的直流电路,则电阻的耗散功率(以瓦特为单位)可以通过以下任一通用公式得出:
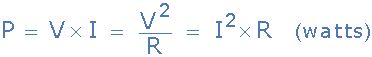
其中:V是直流电压,I是直流电流,R是电阻值。
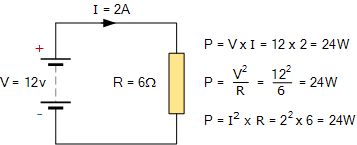
因此,只有当电压和电流同时存在时,电路中的功率才存在,即没有开路或闭路条件。考虑以下标准电阻直流电路的简单示例:
直流电阻电路
交流电路中的电力在直流电路中,电压和电流通常是恒定的,不会随时间变化,因为没有与电源相关的正弦波形。但是,在交流电路中,电压,电流和功率的瞬时值受电源的影响而不断变化。因此,我们无法以与直流电路相同的方式来计算交流电路中的功率,但仍可以说功率(p)等于电压(v)乘以安培(i)。
另一个重要的一点是,交流电路包含电抗,因此存在功率成分,这是由该成分产生的磁场和/或电场造成的。结果是,与纯电阻组件不同,该功率被存储,然后在正弦波形经过一个完整的周期周期后返回电源。
因此,电路吸收的平均功率是一个完整周期内存储的功率与返回的功率之和。因此,电路的平均功耗将是一个完整周期内瞬时功率与瞬时功率的平均值p,瞬时功率p定义为瞬时电压v与瞬时电流i的乘积。请注意,由于正弦函数是周期性且连续的,因此在所有时间内给出的平均功率将与在单个周期内给出的平均功率完全相同。
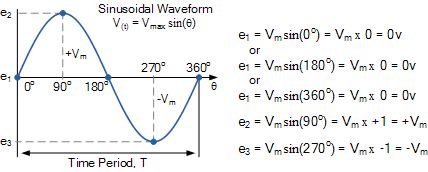
让我们假设电压和电流的波形都是正弦波,因此我们回想一下:
正弦电压波形
由于瞬时功率是任何时刻的功率,因此:
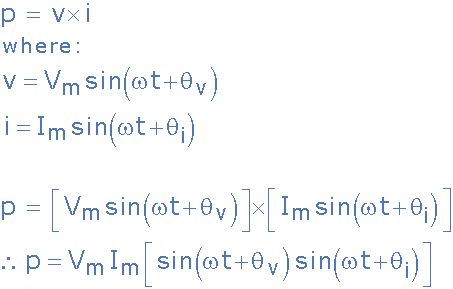
应用以下公式的三角积和和:
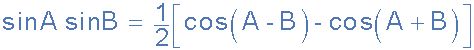
和θ =θ v - θ 我入上式(电压和电流波形之间的相位差)给出:
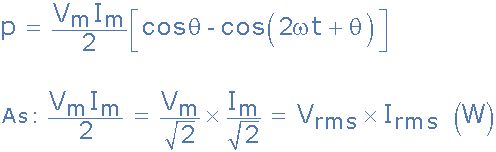
其中V和I分别是正弦波形的均方根(rms)值,v 和i,θ是两个波形之间的相位差。因此,我们可以将瞬时功率表示为:
瞬时交流功率方程

该方程式向我们显示瞬时交流功率具有两个不同的部分,因此是这两个项的总和。第二项是随时间变化的正弦曲线,由于项的2ω部分,其频率等于电源角频率的两倍。但是,第一项是一个常数,其值仅取决于电压(V)和电流(I)之间的相位差θ。
由于瞬时功率会随着时间的变化而正弦曲线的轮廓不断变化,因此很难进行测量。因此,在数学上使用幂的平均值或平均值更方便,也更容易。因此,在固定的周期数内,正弦曲线瞬时功率的平均值简单地表示为:
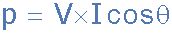
其中V和I是正弦有效值,而θ(Theta)是电压和电流之间的相角。功率单位为瓦特(W)。
如图所示,也可以使用流过电路的电压V rms或电流I rms,从电路的阻抗(Z)中找到在电路中耗散的交流电源。
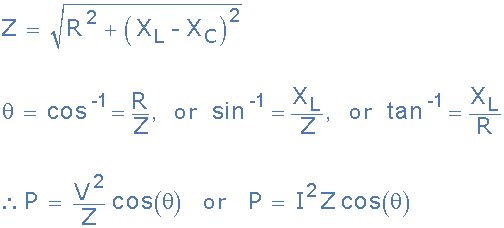
交流电路中的电源(二)
50Hz正弦电源的电压和电流值分别为:v t = 240 sin(ωt+60°)Volts和i t = 5 sin(ωt-10°)Amps。求出电路的瞬时功率和平均功率值。
由上可知,电路吸收的瞬时功率为:
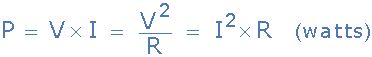
从上面应用三角恒等式规则可得出:

然后计算平均功率为:

您可能已经注意到205.2瓦的平均功率值也是瞬时功率p(t)的第一项值,因为该第一项常数值是电源和负载之间的平均或平均能量变化率。
纯电阻电路中的交流电源
到目前为止,我们已经看到,在直流电路中,功率等于电压和电流的乘积,这种关系对于纯电阻交流电路也是如此。电阻器是消耗能量的电气设备,电阻器中的功率由p = VI = I 2 R = V 2 / R给出。这种力量永远是积极的。
如图所示,考虑下面的纯电阻性电路(即,无穷大电容,C =∞,零电感,L = 0),其电阻器连接到交流电源。
纯电阻电路
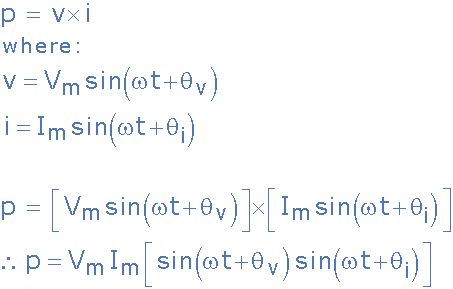
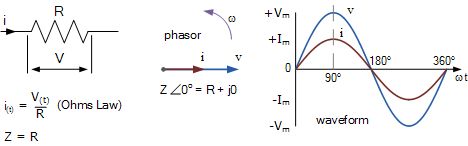
当将纯电阻器连接到正弦电压电源时,流经电阻器的电流将与电源电压成比例地变化,即电压和电流波形彼此“同相”。由于电压波形和电流波形之间的相位差为0 o,导致cos 0°的相位角等于1。
然后,电阻器消耗的电能为:
纯电阻中的电能
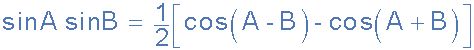
由于电压和电流波形是同相的,即两个波形同时达到其峰值,并且同时也通过零,因此上面的功率方程式减小为:V * I。因此,可以通过将两个波形相乘得到伏安乘积来找到任意时刻的功率。这称为“有功功率”,以瓦特(W),千瓦(kW),兆瓦(MW)等度量的(P)。
纯电阻的交流电源波形
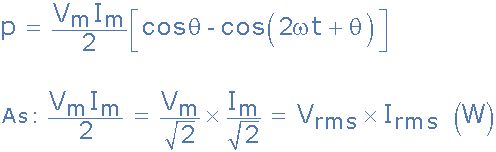
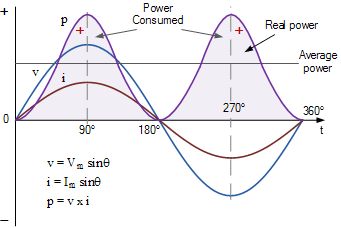
该图显示了电压,电流和相应的功率波形。由于电压波形和电流波形都是同相的,因此在正半周期内,当电压为正时,电流也为正,因此功率为正,正数乘以正数就等于正数。在负半周期内,电压为负,导致功率为正的电流也为负,因为负乘以负就等于正。
然后,在纯电阻电路中,在电流流过电阻器的所有时间中都会消耗电能,并表示为:P = V * I = I 2 R瓦。请注意,V和I都可以是其均方根值,其中:V = I * R和I = V / R
纯感应电路中的交流电源
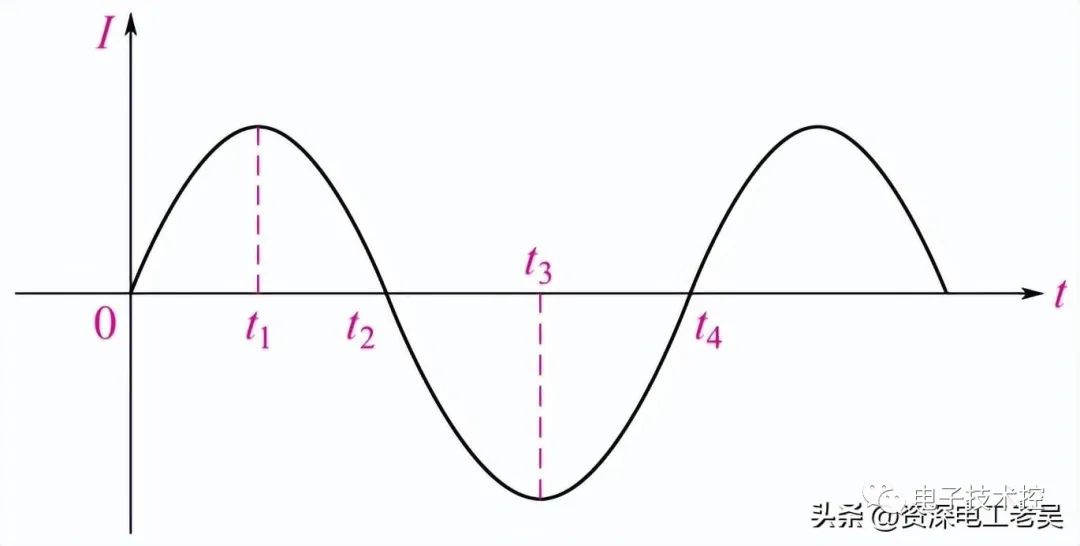
在L Henries的纯电感性电路(即,无穷大电容,C =∞,零电阻,R = 0)中,电压和电流波形不是同相的。每当将变化的电压施加到纯感应线圈上时,由于其自感,线圈会产生“反”电动势。这种自感与线圈中流动的电流相反并限制了其变化。
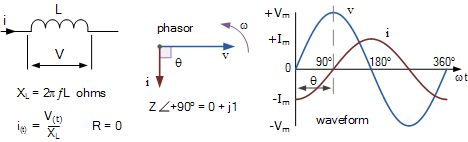
反电动势的作用是,电流不能立即与施加的电压同相地通过线圈,从而导致电流波形在电压峰值之后的某个时间达到其峰值或最大值。结果是,在纯电感电路中,如图所示,电流总是在电压之后“滞后”(ELI)90°(π/ 2)。
纯感应电路

上面的波形向我们展示了纯电感线圈上的瞬时电压和瞬时电流随时间的变化。最大电流I max出现在电压的最大值(峰值)之后的一个四分之一周期(90°)内。此处显示的电流在电压周期开始时具有负的最大值,并且当电压波形在90°处达到最大值时,通过零增加到其正的最大值。
因此,由于电压和电流波形不再一起上升和下降,而是在线圈中引入了90°(π/ 2)的相移,因此电压和电流波形彼此“异相”另一种是电压使电流领先90°。由于电压波形和电流波形之间的相位差为90°,因此相位角导致cos 90° = 0。
因此,由一个纯电感器Q L存储的电能由下式给出:
纯电感中的有功功率
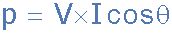
显然,纯电感器不会消耗或消耗任何有功或有功功率,但是由于我们同时具有电压和电流,因此在表达式中使用cos(θ):P = V * I * cos(θ)不再有效。在这种情况下,电流和电压的乘积是虚功率,通常称为“无功功率”,(Q)以无功伏安(VAr),千伏无功(KVAr)等度量。
伏安无功,VAr不应与用于有功功率的瓦特(W)混淆。VAr代表彼此异相90°的伏特和安培数的乘积。为了在数学上识别无功平均功率,使用了正弦函数。然后,电感中平均无功功率的等式变为:
纯电感中的无功功率
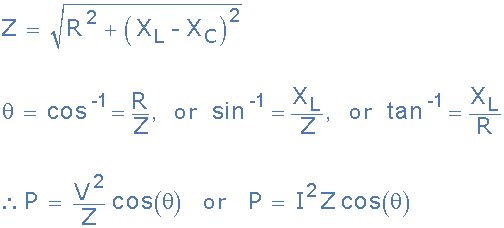
像有功功率(P)一样,无功功率(Q)也取决于电压和电流,还取决于它们之间的相位角。因此,它是所施加电压与电流分量的乘积,该分量与所示电压异相90°。
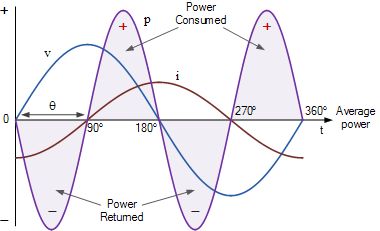
纯电感器的交流电源波形

在0°和90°夹角之间的电压波形的正一半中,电感电流为负,而电源电压为正。因此,伏特和安培乘积给出的负功率为负乘以正等于负。在90 °和180°之间,电流和电压波形均为正值,从而产生正功率。该正功率表示线圈正在消耗电源的电能。
在介于180°和270°之间的电压波形的负一半中,存在负电压和表示负功率的正电流。该负功率表示线圈正在将存储的电能返回给电源。在270°和360°之间,电感器电流和电源电压均为负值,从而导致一段正功率。
然后,在电压波形的一个完整周期内,我们有两个相同的正负功率脉冲,其平均值为零,因此,由于功率交替往返于电源,因此没有实际功率用完。这意味着纯电感器在一个完整周期内所消耗的总功率为零,因此电感器的无功功率不会执行任何实际工作。
纯电容电路中的交流电源C Farads的纯电容性电路(电感为零,L = 0,无穷大电阻,R =∞)具有延迟电路两端电压变化的特性。电容器以电介质形式的电场形式存储电能,因此纯电容器不会耗散任何能量,而是将其存储起来。
在纯电容电路中,电压不能与电流同相增加,因为它需要首先“充电”电容器极板。这导致电压波形在电流波形之后的某个时间达到其峰值或最大值。结果是,在纯电容电路中,电流始终将电压“领先”(ICE)90°(ω/ 2),如图所示。
纯电容电路

然后计算平均功率为:
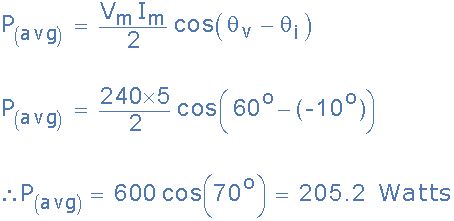
您可能已经注意到205.2瓦的平均功率值也是瞬时功率p(t)的第一项值,因为该第一项常数值是电源和负载之间的平均或平均能量变化率。
纯电阻电路中的交流电源
到目前为止,我们已经看到,在直流电路中,功率等于电压和电流的乘积,这种关系对于纯电阻交流电路也是如此。电阻器是消耗能量的电气设备,电阻器中的功率由p = VI = I 2 R = V 2 / R给出。这种力量永远是积极的。
如图所示,考虑下面的纯电阻性电路(即,无穷大电容,C =∞,零电感,L = 0),其电阻器连接到交流电源。
纯电阻电路
当将纯电阻器连接到正弦电压电源时,流经电阻器的电流将与电源电压成比例地变化,即电压和电流波形彼此“同相”。由于电压波形和电流波形之间的相位差为0 o,导致cos 0°的相位角等于1。
然后,电阻器消耗的电能为:
纯电阻中的电能
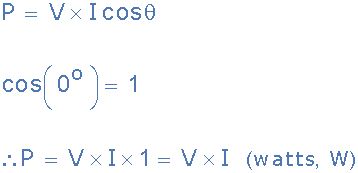
由于电压和电流波形是同相的,即两个波形同时达到其峰值,并且同时也通过零,因此上面的功率方程式减小为:V * I。因此,可以通过将两个波形相乘得到伏安乘积来找到任意时刻的功率。这称为“有功功率”,以瓦特(W),千瓦(kW),兆瓦(MW)等度量的(P)。
纯电阻的交流电源波形
该图显示了电压,电流和相应的功率波形。由于电压波形和电流波形都是同相的,因此在正半周期内,当电压为正时,电流也为正,因此功率为正,正数乘以正数就等于正数。在负半周期内,电压为负,导致功率为正的电流也为负,因为负乘以负就等于正。
然后,在纯电阻电路中,在电流流过电阻器的所有时间中都会消耗电能,并表示为:P = V * I = I 2 R瓦。请注意,V和I都可以是其均方根值,其中:V = I * R和I = V / R
纯感应电路中的交流电源
在L Henries的纯电感性电路(即,无穷大电容,C =∞,零电阻,R = 0)中,电压和电流波形不是同相的。每当将变化的电压施加到纯感应线圈上时,由于其自感,线圈会产生“反”电动势。这种自感与线圈中流动的电流相反并限制了其变化。
反电动势的作用是,电流不能立即与施加的电压同相地通过线圈,从而导致电流波形在电压峰值之后的某个时间达到其峰值或最大值。结果是,在纯电感电路中,如图所示,电流总是在电压之后“滞后”(ELI)90°(π/ 2)。
纯感应电路
上面的波形向我们展示了纯电感线圈上的瞬时电压和瞬时电流随时间的变化。最大电流I max出现在电压的最大值(峰值)之后的一个四分之一周期(90°)内。此处显示的电流在电压周期开始时具有负的最大值,并且当电压波形在90°处达到最大值时,通过零增加到其正的最大值。
因此,由于电压和电流波形不再一起上升和下降,而是在线圈中引入了90°(π/ 2)的相移,因此电压和电流波形彼此“异相”另一种是电压使电流领先90°。由于电压波形和电流波形之间的相位差为90°,因此相位角导致cos 90° = 0。
因此,由一个纯电感器Q L存储的电能由下式给出:
纯电感中的有功功率
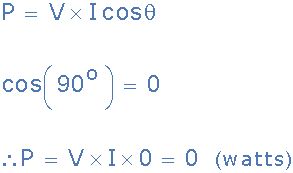
显然,纯电感器不会消耗或消耗任何有功或有功功率,但是由于我们同时具有电压和电流,因此在表达式中使用cos(θ):P = V * I * cos(θ)不再有效。在这种情况下,电流和电压的乘积是虚功率,通常称为“无功功率”,(Q)以无功伏安(VAr),千伏无功(KVAr)等度量。
伏安无功,VAr不应与用于有功功率的瓦特(W)混淆。VAr代表彼此异相90°的伏特和安培数的乘积。为了在数学上识别无功平均功率,使用了正弦函数。然后,电感中平均无功功率的等式变为:
纯电感中的无功功率
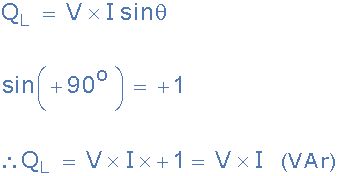
像有功功率(P)一样,无功功率(Q)也取决于电压和电流,还取决于它们之间的相位角。因此,它是所施加电压与电流分量的乘积,该分量与所示电压异相90°。
纯电感器的交流电源波形
在0°和90°夹角之间的电压波形的正一半中,电感电流为负,而电源电压为正。因此,伏特和安培乘积给出的负功率为负乘以正等于负。在90 °和180°之间,电流和电压波形均为正值,从而产生正功率。该正功率表示线圈正在消耗电源的电能。
在介于180°和270°之间的电压波形的负一半中,存在负电压和表示负功率的正电流。该负功率表示线圈正在将存储的电能返回给电源。在270°和360°之间,电感器电流和电源电压均为负值,从而导致一段正功率。
然后,在电压波形的一个完整周期内,我们有两个相同的正负功率脉冲,其平均值为零,因此,由于功率交替往返于电源,因此没有实际功率用完。这意味着纯电感器在一个完整周期内所消耗的总功率为零,因此电感器的无功功率不会执行任何实际工作。
纯电容电路中的交流电源C Farads的纯电容性电路(电感为零,L = 0,无穷大电阻,R =∞)具有延迟电路两端电压变化的特性。电容器以电介质形式的电场形式存储电能,因此纯电容器不会耗散任何能量,而是将其存储起来。
在纯电容电路中,电压不能与电流同相增加,因为它需要首先“充电”电容器极板。这导致电压波形在电流波形之后的某个时间达到其峰值或最大值。结果是,在纯电容电路中,电流始终将电压“领先”(ICE)90°(ω/ 2),如图所示。
纯电容电路
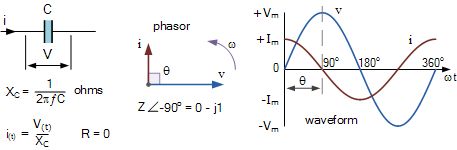
该波形向我们显示了纯电容器两端的电压和电流随时间的变化。最大电流Im出现在电压的最大值(峰值)之前的一个四分之一周期(90°)。此处显示的电流在电压周期开始时具有正的最大值,并且流过零,当电压波形在90°处达到最大值时减小到其负的最大值。与纯感应电路相反的相移。
因此,对于纯电容性电路,相角θ= -90°,电容器中平均无功功率的等式变为:
纯电容器中的无功功率
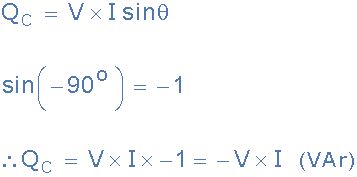
其中–V * I * sin(θ)是负正弦波。同样,容性无功功率的符号是Q C,其度量单位相同,即与电感器相同的伏安无功(VAR)。然后我们可以看到,就像上面的纯电感电路一样,纯电容器不会消耗或消耗任何有功功率或有功功率P。
纯电容器的交流电源波形
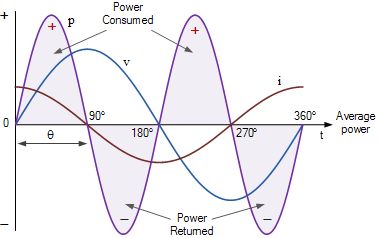
在0的角度之间的电压波形的正半周和90°,无论是电流和电压波形是在产生正功率值正被消耗。在90°至180°之间,电容器电流为负,电源电压仍为正。因此,伏安乘积给出的负功率为负乘以正等于负。该负功率表示线圈正在将存储的电能返回给电源。
在介于180°和270°之间的电压波形的负一半中,电容器电流和电源电压均为负值,从而导致一段正功率。这个正功率周期表示线圈正在消耗电源的电能。在270°和360°之间,存在负电压和正电流,再次表示负功率。
然后,在电压波形的一个完整周期内,存在与纯电感电路相同的情况,因为我们有两个相同的正负功率脉冲,其平均值为零。因此,从电源到电容器的功率恰好等于电容器返回电源的功率,因此没有实际功率用完,因为功率交替地流入和流出电源。这意味着纯电容器在一个完整周期内所消耗的总功率为零,因此电容器的无功功率不会执行任何实际工作。
电源示例2
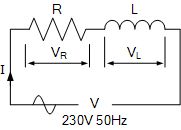
电阻为30欧姆,电感为200mH的电磁线圈连接到230VAC,50Hz电源。计算:(a)螺线管阻抗,(b)螺线管消耗的电流,(c)电流与施加电压之间的相角,以及(d)螺线管消耗的平均功率。
给出的数据为:R =30Ω,L = 200mH,V = 230V和ƒ= 50Hz。
(a)电磁线圈的阻抗(Z):
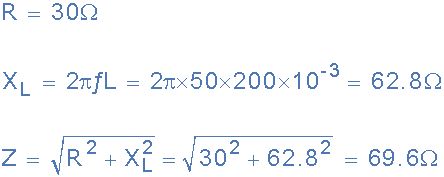
(b)电磁线圈消耗的电流(I):
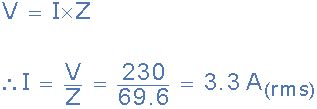
(c)相角θ:
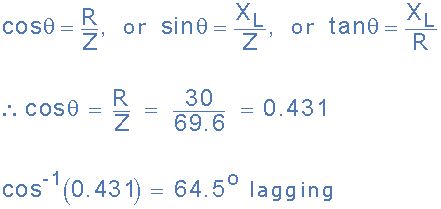
(d)电磁线圈平均消耗的交流功率:

交流电源摘要我们在这里已经看到,在交流电路中,纯无源电路中流动的电压和电流通常是异相的,因此,它们不能用于完成任何实际工作。我们还看到,在直流(DC)电路中,电功率等于电压乘以电流,即P = V * I,但是我们无法按照与交流电路相同的方式进行计算。考虑任何相位差,在纯电阻电路中,电流和电压都是同相的,并且电阻通常将所有电能消耗为热量。最后,没有电力返回到电源或电路。
因此,在包含电抗的纯电感或纯电容电路中,(X)电流将使电压超前或滞后恰好为90°(相角),因此功率既被存储又返回电源。因此,在一个完整的周期内计算出的平均功率将等于零。电阻(R)消耗的电功率称为有功功率或有功功率,只需将均方根电压乘以均方根电流即可获得。电抗所存储的功率(X)称为无功功率,是通过将它们之间的电压,电流和相角的正弦值相乘而获得的。相角的符号是θ(Theta),它表示AC电路相对于总无功阻抗(Z)的低效率,该阻抗与电路中的电流相反。
责任编辑人:CC
-
电源技术
+关注
关注
5文章
564浏览量
44579 -
交流电路
+关注
关注
0文章
184浏览量
28835
原文标题:交流电路中的电源
文章出处:【微信号:A1411464185,微信公众号:multisim】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
交流电路中电容和阻抗之间的关系,如何计算电容器的阻抗?




 一文详解交流电路中的电源技术
一文详解交流电路中的电源技术
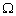











评论