2020年10月16日下午,中共中央政治局举行第二十四次集体学习,主题是“量子科技研究和应用前景”。为更好地了解国内外量子密码科技发展态势,更好地推进我国量子科技发展,本专委会邀请广东工业大学的教授专门撰文介绍后量子密码技术。
一、后量子密码技术的发展历程
后量子密码技术是指可以抵抗量子计算机攻击的密码技术。所谓“后”,是指在大规模稳定的量子计算机出现后,现有的绝大多数公钥密码算法(RSA、Diffie-Hellman、椭圆曲线等)将会被攻破,只有能抵抗这种攻击的密码算法可以在进入量子计算时代之后存活,因此也称为“抗量子密码技术”。
近年来,量子计算机的发展非常迅速,许多大学或企业如加州大学、Google、IBM、Intel等为之都投入了大量人力物力[1]。
2007年,加拿大一家名为D-Wave System的公司已经造出了一台量子计算机D-Wave,尽管人们还在争论这台计算机是否能达到原理上所要求的特性与效果(即无法使所有量子比特发生纠缠),但NASA和Google已经测试出这台计算机在解决某些问题上比传统的单核计算机快1亿倍 [2]。
2014年,Google的研究团队宣布建成9量子比特的可编程量子机器,直到2018年3月,该研究团队发布了新的72量子比特的量子处理器Bristlecone,标志着量子计算技术的发展进入了一个极速发展的阶段。与此同时,IBM公司也宣称他们已经成功开发出一台50量子比特的原型机,该50量子比特的量子计算机能vwin 传统计算机的所有操作。
在国内,2017年5月,阿里巴巴与中科院、中科大合作团队研发出10 量子比特的线路样品。
2018年2月,阿里合作团队宣布11量子比特超导量子计算服务将在阿里的量子计算云平台上线。
一般来说,密码系统在开发过程中都会考虑到破解其的计算技术发展的速度和水平,传统密码的安全性依赖于某些问题对现代计算机的难解性,例如,RSA依赖于大数因式分解难题。传统的计算机采用二进制数即0和1来处理信息,因此处理一个1024位的大数(0-21024)因式分解是一个难解问题。但量子计算机不同,它利用量子力学,并使用 “量子位元”而不是0和1来处理信息。因此,在处理大数因子分解时,量子计算机会有更好的效果。图1展示了量子计算机对现有密码标准的影响。
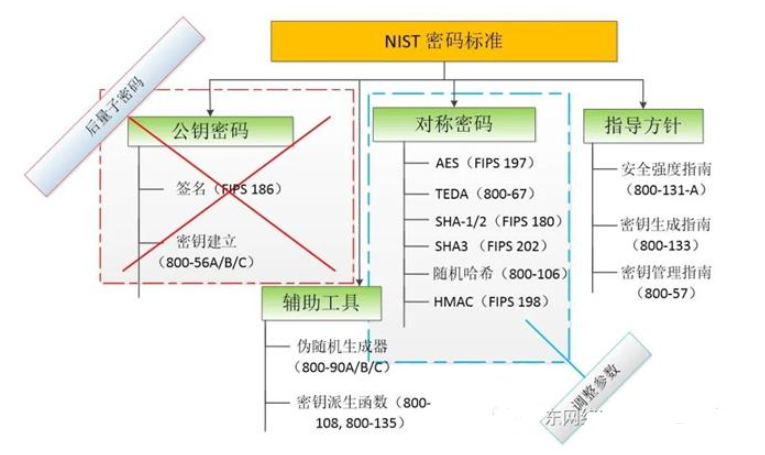
图1 量子计算机对现有密码标准的影响
其中:红色叉,代表量子计算机可以完全攻破,需要后量子密码算法代替;蓝色框,不那么紧迫需要新算法代替,可以通过调整算法参数解决。
总的来说,量子计算机对现有密码标准的影响有以下几个要点:
1.对于公钥密码算法,量子计算机对安全性的影响包括:
(1)完全攻破目前广泛使用的公钥密码算法。公钥密码算法安全性依赖的数学问题可以被高效的量子算法所解决。由于底层依赖的数学问题被解决,所以这些公钥密码算法不再安全。这些数学问题包括:离散对数 (及椭圆曲线版本)、大整数分解等。这直接影响目前使用的 RSA、Diffie-Hellman、椭圆曲线等算法。着名的量子算法是1994年的Shor‘s algorithm[4]。
(2)增大密钥参数的长度没有用。增大密钥长度对于现有的传统计算机和攻击算法是可以的,但对于量子计算机和算法,这是徒劳的。
(3)需要全新的公钥密码算法即后量子密码算法。
2.对于对称密码算法,量子计算机对安全性的影响:
(1)降低现有算法的安全性:安全性减半。关于对称密码算法和哈希函数(例如 AES、SHA1、SHA2 等),虽然有量子算法可以理论上攻破,但这个算法的影响有限,且有很多限制条件。着名的量子算法是1996年的Grover’s algorithm[5],可将安全性从k-bit 降低为k/2-bit。
(2)增大参数的长度有用,把密钥长度或哈希的长度加倍即可,例如:AES-128升级至AES-256,SHA-256升级至SHA-512等。
3.量子计算机具有强大的算力,但利用的前提是:存在能高效解决问题的量子算法,否则量子计算机没什么用,反而因为其高昂的成本带来劣势。
4.量子比特数量重要,但更重要的是质量。目前建造的量子计算机(例如 Google 的 72 量子位芯片)中,量子物理比特的质量较差。由于量子相干等物理机制,必须引入纠错机制,但需要成百上千个量子物理比特进行纠错,来实现一个量子逻辑比特的功能。
5.攻破现有的公钥密码算法需要几千甚至几万个逻辑比特,而建造量子计算机目前仍处在很初级的阶段。
6.对于某些量子算法(例如 Grover),需要指数级别的内存,因此 Grover 算法的威胁不如Shor的算法那么紧迫。
二、后量子密码的技术现状
密码学界在研究可以抵抗量子计算机攻击的密码算法方面,最早可以追溯到 1978年的 McEliece加密、Merkle哈希签名等算法。但那时量子计算机对密码算法的威胁并没有很明确,也没有“后量子”的概念,直到最近十几年,后量子密码的重要性逐渐显现出来。
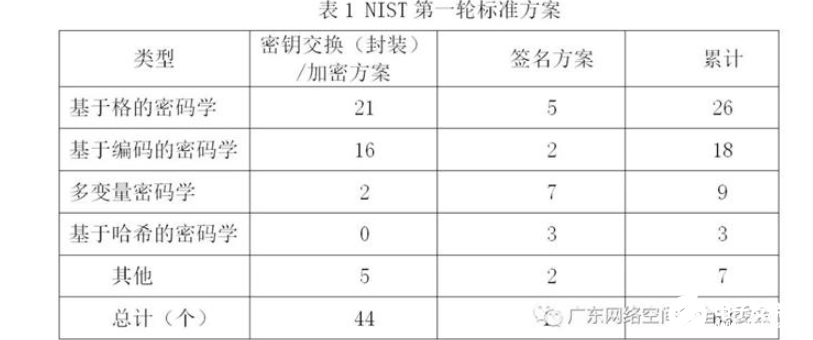
2016年秋,美国国际标准技术研究所(NIST)发布后量子领域标准化方案征求稿[6],正式在全球范围征集后量子密码学标准协议。2017年12月,NIST公布后量子密码学标准协议的第一轮预选协议,协议均为后量子密码学基础方案,即加密(含密钥交换KE或密钥封装KEM)和签名方案。此次共收到82个基础方案,其中公开69个被认为是完整的方案,随后6个被撤销。第一轮标准中基于格的密码学方案有26个,基于编码的密码学方案有18个,多变量密码学方案有9个,基于哈希的密码学方案有3个,以及其他类型密码学方案有7个。具体情况如表1所示。
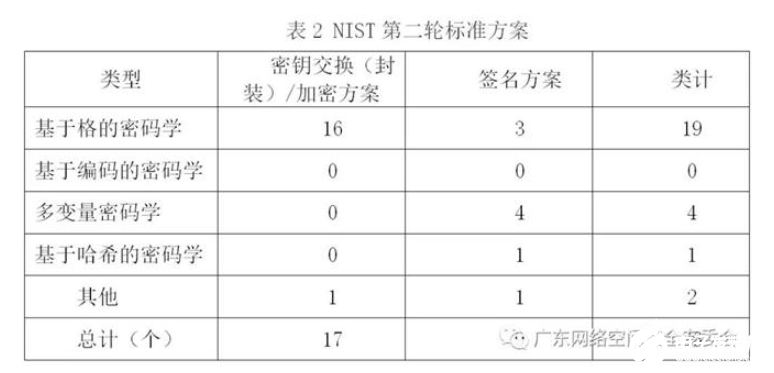
2018年11月,NIST再次发布第二轮的标准方案,从第一轮标准方案以及最新研究成果中遴选出26个进入第二轮,其中包括17个公钥加密和密钥交换方案及9个数字签名方案。具体情况如表2所示。
在NIST候选方案中,主要包括以下四种数学方法构造的后量子密码算法:基于哈希的公钥密码学、基于编码的公钥密码学、基于多变量的公钥密码学以及基于格的公钥密码学。
1. 基于哈希 (Hash-based)的公钥密码学
基于哈希的签名算法最早出现于1979年,被认为是传统数字签名 (RSA、DSA、ECDSA等)的可行代替算法之一[7]。该方案使用哈希函数的输入作为私钥,输出作为公钥。这些密钥仅适用于一个签名,因为签名本身会显示密钥的一部分。基于哈希的签名会使用Merkle树认证机制来减少空间消耗。使用Merkle树认证后,哈希树的根是公钥,一次性的签名密钥是树中的叶子节点。基于哈希的签名算法的安全性依赖哈希函数的抗碰撞性,由于没有有效的量子算法能快速找到哈希函数的碰撞,因此(输出长度足够长的)基于哈希的构造可以抵抗量子计算机攻击。此外,基于哈希的数字签名算法的安全性不依赖某一个特定的哈希函数。即使目前使用的某些哈希函数被攻破,也可以用更安全的哈希函数直接代替被攻破的哈希函数。
例如,一个经典的基于哈希的签名方案设计如下图2所示。
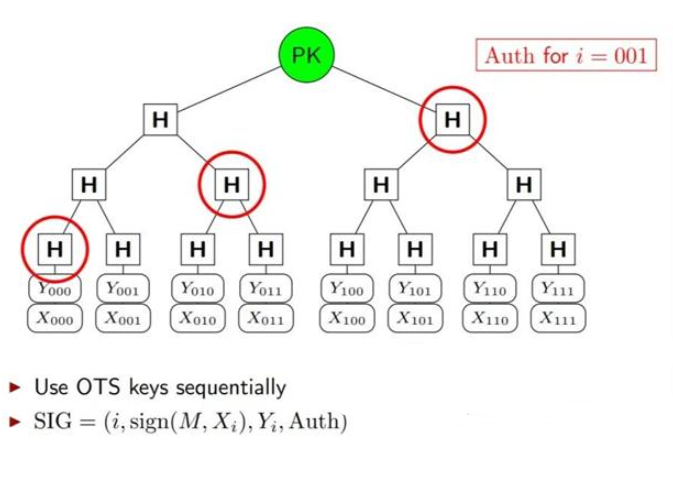
图2 基于哈希的签名方案设计图
方案中的Xi和Yi分别为一次性密钥的私钥和公钥,对消息的签名增加了两个状态参数i和Auth,i用来保证所有叶子不会被使用超过1次,Auth是路径,用来存储中间结果,能使签名快速运行。
基于哈希的代表算法有:Merkle 哈希树签名、XMSS、Lamport签名等。
2.基于编码 (Code-based) 的公钥密码学
基于编码的算法最早出现于1978年,主要用于构造加密算法。目前技术方向主要分为两种:基于海明度量(Hamming metric)的编码方案和基于秩度量(Rank metric)的编码。
基于海明度量的编码方案的数学困难假设是校验子译码问题(Syndrome Decoding Problem)。校验子译码问题已被证明为NP完全(NP-Complete)问题[8]。此方向一个着名的加密算法是 McEliece [9],该方案使用了Goppa Codes,迄今为止仍然是安全的设计方案。但该方案最大的缺点就在于其公钥需要1MB左右的大小才能达到256bit的安全度。
目前NIST标准预选方案中,大部分是基于秩度量的编码方案。基于此技术而建构的加密或密钥交换方案包括Loi17[10]、RQC[11]、ROLLO[12]、LG[13]和McNie [14]等等。我国在秩度量加密方案的设计方面也有进展,如中科院信工所研究员设计的两项加密方案:Piglet[15]和Loong[16]。
基于编码的代表算法有:McEliece、Loi17、ROLLO等。
3. 基于多变量 (Multivariate-based) 的公钥密码学
基于多变量的算法使用有限域上具有多个变量的二次多项式组构造加密、签名、密钥交换等算法[17]。多变量密码的安全性依赖于求解非线性方程组的困难程度,即多变量二次多项式问题。该问题已被证明为非确定性多项式时间(NP)困难。目前没有已知的经典和量子算法可以快速求解有限域上的多变量方程组。与经典的基于数论问题的密码算法相比,基于多变量的算法的计算速度快,但公钥较大,因此适用于无需频繁进行公钥传输的应用场景(如物联网设备等)。
多变量密码的基础方案设计就形式来说,可以分为两种形式。
一种是既基于MQ 又基于IP (Isomorphism of Polynomials,多项式同构)问题的MPKC 加密或签名方案设计,该方向的设计思路和密码分析方法等都较为成熟,因而产生了较多的研究成果,如Rainbow[18],UOV[19],LUOV[20],PFlash[21]等,以及近年基于大域上变量平方构造的SQUARE[22],EFC[23],使用了双重HFE 的ZHFE[24],Simple Matrix(ABC)加密方案[25],Cubic ABC 加密方案[26],基于中间域(大域小域特点结合的思想)的多变量加密方案有中国的[27][28]等。
另一种是基于新设计思路、困难问题的方案设计。虽然目前基于IP问题设计MPKC方案依然是主流,但在设计思路与安全分析都相对成熟的情况下,取得突破性的成就反而不容易。因此MPKC 也需要提出一些新的设计思路,提出一些新的困难性假设来保持这个领域的活力和创新性。比如在PKC2012,有文献结合格密码中LWE的一些特性提出了一种新的困难性假设问题[29],并在此困难性假设下提出了一种安全的加密方案。而在2014 年的Asia crypt会上有学者提出了一种不同于IP或者IP1S 的全新MPKC 设计结构ASASA [30],设计结合了对称密码中的S盒(使用二次多项式构造)以及A(仿射的)的构造特点。在国际顶级会议CRYPTO 2011 上,则有文献提出了一种身份识别方案[31],它的安全性依赖于非交互的承诺方案的存在性, 并给出了形式化的可证安全。从该身份识别方案出发,有学者通过Fiat-Shamir转换构造了后量子第一轮标准签名方案MQDSS[32]。该类型的密码方案还包括最近基于新困难问题的第一轮标准协议Giophantus[33]。此外,我国方面,基于Hyper-Sphere 超球面方程的多变量方案则可以用于群组签名的设计并提出了相关的安全性证明[34],武汉大学有教授提出了一个可证安全的基于多项式同态(Morphism of polynomials, MP)的密钥交换协议[35]等等。
基于多变量的代表算法有:LUOV、Rainbow、MQDSS等。
4. 基于格 (Lattice-based) 的公钥密码学
在后量子加密的所有方法中,对格的研究是最活跃和最灵活的。这是因为基于格的算法在安全性、公私钥大小、计算速度上达到了更好的平衡[36]。与基于数论问题的密码算法构造相比,基于格的算法可以实现明显提升的计算速度、更高的安全强度和略微增加的通信开销 [37]。与其他几种实现后量子密码的方式相比,格密码的公私钥更小,并且安全性和计算速度等指标更优。此外,基于格的算法可以实现加密、数字签名、密钥交换、属性加密、函数加密、全同态加密等各类功能的密码学构造。
基于格的算法的安全性依赖于求解格中问题的困难性。这些问题在达到相同的安全强度时,基于格的算法的公私钥大小比上述三种结构的方法更小,计算速度也更快,且能被用于构造多种密码学原语,因此更适用于真实世界中的应用。
近年来,基于LWE(Learning with Errors) 问题 [38] 和 RLWE (Ring-LWE) 问题[39]的格密码学构造发展迅速,被认为是最有希望被标准化的技术路线之一。
基于格的代表算法有:Kyber、Dilithium、NTRU系列、NewHope(Google 测试过)、一系列同态加密算法 (BGV、GSW、FV等)。
下表中给出了四种后量子密码算法的简要对比:
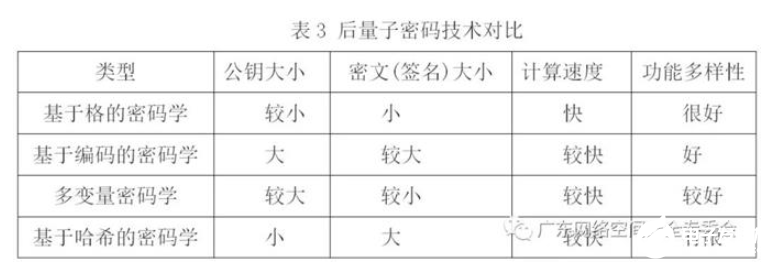
表中的对比反映出该类后量子密码算法的平均性能指标。在实际应用中具体采用哪个类别/哪个算法更好,需要针对应用场景进行详细分析。例如,在一些频繁需要交换公钥的场景(例如 HTTPS),可以使用 Lattice-based 的算法等。
除这四种类型的后量子密码技术之外,还有基于超奇异椭圆曲线 (Supersingular elliptic curve isogeny)、量子随机漫步 (Quantum walk)等技术的后量子密码构造方法。
三、后量子密码的发展前景
近年来,欧洲国家的“安全密码”(SafeCrypto)项目和日本的CREST密码数学项目都取得了显着成果,美国NIST的“后量子密码”(PQCrypto)项目和处于后量子密码研究和应用领域的领先地位。
对于后量子密码的发展前景大致如下。
1. 公钥密码系统向后量子密码系统的稳步推进
传统计算技术和量子计算技术的进步,推动了对更强大密码技术的需求。为了抵御对传统计算的攻击,NIST已经建议从提供80位安全性的密钥大小和算法过渡到提供112位或128位安全性的密钥大小和算法。而为了提供抵御量子攻击的安全性,未来还需要进行一个过渡,即把公钥密码系统过渡到新的后量子密码系统。
欧洲电信标准协会与加拿大滑铁卢大学量子计算中心联合举办的量子安全密码工作组会议(IQC/ETSI Quantum-Safe Crypto Workshop)也在国际后量子密码研究领域产生了重要影响。该会始于2013年,参会代表来自于数学、密码学、物理学、计算机等不同研究领域,目标是实现标准化和部署下一代密码基础设施,特别是抵御量子计算能力威胁的冲击。
2. 后量子密码技术标准制定逐步受到政府组织的重视
后量子密码学标准的制定将需要大量的资源分析候选的抗量子计划,为了确保对算法的信任,需要大量的研究人员参与密码分析。国际上对量子计算和后量子密码学领域的兴趣最近有所增加,这跟量子计算硬件的发展和各国国家安全局最近对后量子标准的政策制定有关,大致总结如下。
美国方面,2015年8月,美国国家安全局公开宣布由于面临量子计算的威胁,其计划将联邦政府各部门目前使用的ECC/RSA算法体系向后量子算法进行迁移。而负责标准制定的NIST则在2016年2月正式面向全球公开了后量子密码标准化的路线图,并在同年秋正式公布征集密码方案建议的计划,其中包括公钥密码、数字签名以及密钥交换算法。2017年12月获得第一轮的建议方案;2018年12月征集后得到第二轮的建议方案;NIST会利用3-5年时间分析这些建议并发布相关分析报告,最终的标准拟制工作也将耗时1-2年。换言之,美国国家标准与技术局的后量子密码算法标准最终可能会在2021-2023年出台。
欧洲量子密码学术和工业界研究者联合组织“后量子密码”项目(PQCrypto)在2015年发布了一份初始报告,在对称加密、对称授权、公钥加密以及公钥签名系统领域都提出了相关标准化建议。
我国方面,从2018年12月开始,中国密码学会在国家密码管理局的指导下,启动全国密码算法设计竞赛[40],其中包含分组密码算法设计和公钥密码算法设计两部分。而后者则主要是后量子密码算法的设计,当年即收到第一轮共38个公钥密码算法设计,并于2019年10月从中遴选出第二轮12个算法。
3. 企业界将在后量子密码发展应用过程中发挥重要影响力
从以往的密码系统标准化发展历史来看,任何密码系统都必须在应用过程中增强和完善性能,后量子密码也不例外。因此,通过新型密码产品的商业化推广使用活动,企业界能够不断积累和分析用户数据,从而促进后量子密码系统安全性能和运行效应的提升。
美国安全创新公司(Security Innovation)注册并拥有NTRU算法的专利,其提供两种授权选项:开源GNUGPL v2授权以及商业授权。从2011年起,该公司发布了多种实现NTRU算法的软件库,其中包括安全套接字协议层(SSL)和ARM7/9处理器库等。NTRU工程(NTRUProject)网站中已经存在使用NTRU加密算法的Java和C程序应用。目前,NTRU算法已经在处理能力有限的移动设备以及大容量服务器中得到应用。
微软公司2016年发布了基于格密码库(Lattice Crypto),这种可移植软件的底层机制是基于环上带误差学习问题(Ring Learning With Errors)。无论对于使用经典计算机或者量子计算机的攻击者,该软件库至少能够实现128位安全性能。谷歌公司在对当前后量子密码技术发展进行调查后,也提出了基于环上带误差学习问题的密钥交换协议。这些工作都对量子密码系统的标准化具有重要影响。
编辑:hfy
-
量子密码技术
+关注
关注
0文章
13浏览量
7335 -
量子技术
+关注
关注
0文章
127浏览量
12770
发布评论请先 登录
相关推荐
“安徽造”量子随机数芯片通过国家密码管理局检测
大研智造 全面剖析焊锡机器人技术应用现状及发展前景

浅谈自动驾驶技术的现状及发展趋势
【《计算》阅读体验】量子计算
2.晶体和振荡器 行业研究及十五五规划分析报告(行业发展现状及“十五五”前景预测)
抵御量子计算机攻击!中国首个!
【量子计算机重构未来 | 阅读体验】 跟我一起漫步量子计算
量子梦
【量子计算机重构未来 | 阅读体验】+ 了解量子叠加原理
【量子计算机重构未来 | 阅读体验】+ 初识量子计算机
万兆电口模块的产业发展现状与前景展望
博捷芯BJCORE:划片机行业背景、发展历史、现状及趋势





 浅谈后量子密码技术的现状及前景
浅谈后量子密码技术的现状及前景











评论