电子产品设计日益轻薄,使得电源模块亦须提升切换频率以缩小体积。藉由傅里叶级数频域分析,研发人员将可掌握切换式降压转换器电源模块输出端涟波变化量,从而搭配最适合的电感和电容,使电路板尺寸与能源效率达到最佳设计。
电子3C产品功能愈来愈丰富且IC制程的进化趋向于低压大电流,使得芯片对电源的涟波及噪声(Ripple Noise)要求更为严谨。数字产品强调轻薄,相对地,电源模块为符合此要求势必提升切换频率以缩小外部零件体积。高频涟波与噪声对数字电路信号的影响势必严重,尤其是影音(Video/Audio)信号及差动对数据传输信号(Differential Pair Signal)。
基于此因素,本文将以傅里叶函数(Fourier Series Expansion)方式来探讨同步交换式降压转换器(Synchronous Step Down Converter)输出电压纹波的波形,并依电容完整等效串联电阻(ESR)、等效串联电感(ESL)、电容值(Capacitance)对应的公式,经由理论推导,有效地分析电源模块输出端纹波成分。
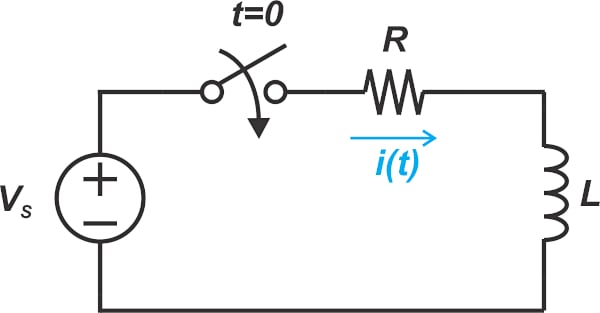
同步降压交换式电源转换器的应用电路如图1所示,系统工作原理是藉由交错式切换High Side (Q1)/Low Side (Q2)金属氧化物场效晶体管(MOSFET)(上、下桥晶体管),将输入能量转换成输出端适当电压以提供到负载侧。系统关键性被动组件电感及输出电容组成的低通滤波器(Low Pass Filter),用于传送与储存能量并滤除交流成分,让输出电压成为平顺的准直流需求。
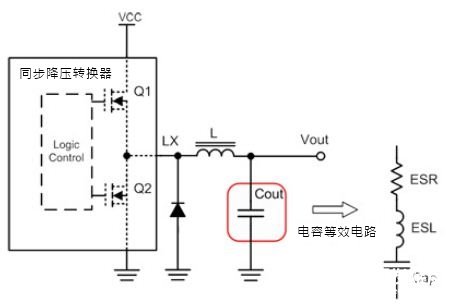
图1同步降压转换器应用电路
在常规技术的认知下,当切换频率愈快,即可得到较小的输出纹波,若以流经电感电流乘上输出电容的等效串联电阻来估算峰值纹波电压是可得到近似数据,但与实际的输出纹波波形有程度上的误差,因此必须考虑电容完整的等效电路特性,便可获得正确的解答。
在切换式降压转换器中,电感电流会对电容充电或放电,因此所有的纹波电流都会流经电容使得输出到负载的电压为稳定的直流电压Vo。然而,实际情形不是如 此,因为实际电容除了本身电容值外,还包含等效串联电阻与等效串联电感参数特性,让输出纹波电压(Ripple Voltage)ΔVo大于默认值,因此欲得到正确的输出纹波,则须将如图1所示完整的电容等效电路加以说明。
其中,Cap全称为Capacitance,意思是电容值,其为电容最主要的参数,应用于电路稳压,补偿或滤噪声之用,可用电容公式来表示其特性,亦即Q = C·Vc或
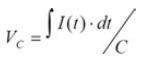
。
而ESR(Equivalent Series Resistance)为等效串联电阻,其为电容能量损耗及纹波的来源,可用欧姆定律来表示其特性,亦即
![]()
。
至于ESL(Equivalent Series Inductance),表示等效串联电感,可用电感微分公式来表示其特性,公式为
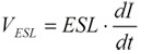
。其感抗正比于频率,在低频时其感抗低,不易观测到其作用,但在频率较高时,其感抗增加,会降低电容稳压滤波的功能。另外要补充的是,I为IL A.C成分,也就是电感电流的交流成分。
一般而言,在稳态(Steady State)及负载固定时,输出电容的纹波电压主要是由电感的纹波电流造成,可先计算出电感的纹波电流,再利用欧姆定律,电感微分公式及电容电荷储存公式,分别计算出ESR、ESL及Capacitance的纹波电压。再将此三种纹波加总起来,便可得输出电容的纹波电压,如公式1所示:

。..。..公式1
电感电流函数IL(t)可由公式2求得,其波形如图2所示。在Ton时(上桥MOSFET导通),输入电源VCC供应能量到负载端且电感组件储存磁能(电感电流为线性递增),依据法拉第定律(Faraday‘s Law):
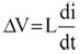
,将可得到导通周期(On-time Duty)电感电流斜率:

图2(A)LX的波形;(B)电感电流的波形;(C)输出纹波波形
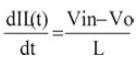
。..。..公式2
在Toff时(下桥MOSFET导通),电感释放能量到负载(电感电流为线性递减);其关断周期(Off-time Duty)电感电流斜率如公式3所示:
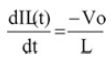
。..。..公式3
应用傅里叶函数频域分析输出纹波波形
依傅里叶级数展开任意周期性函数可得到频率信号的幅度,也代表着信号在不同频率分量成分的大小。频域分析是以输入信号的频率为变量,并能够提供比时域 (Time Domain)信号波形更直观且包含频率、振幅和相位信息。相对的傅里叶变换(Fourier Transform)可将频域函数转换成时域的稳态输出纹波Vo。因此,傅里叶级数与傅里叶变换的优点是可让分析者依所提供的任意输入波形,容易得到输出纹波波形。
周期T傅里叶级数为:
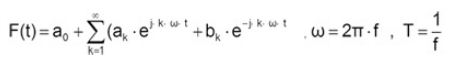
傅里叶系数则是:
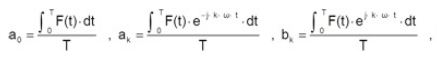
ak及bk是共轭复数。
等效电感阻抗包含ZESR、ZESL、ZCo,计算方式如下所示:

而LX电压波形使用傅里叶级数展开,表示如下:

因此,ESR Ripple傅里叶级数展开如下所示:

ESL Ripple傅里叶级数展开如下所示:

Cap Ripple傅里叶级数展开如下所示:

Vo Ripple傅里叶级数展开如下所示:

应用傅里叶变换数值分析输出电压纹波
在处理信号时,常藉由傅里叶变换来取得信号所对应的频谱,然后再由频谱来读取信号的参数。但由于所做的计算量过于庞大,当处理大量的数据时,则需要快速计 算的算法,因而衍生出快速傅里叶变换(Fast Fourier Transform, FFT)。快速傅里叶变换大幅提高了频谱的计算速度。
快速傅里叶变换的使用条件包括:信号必须是周期性的、取样周期必须为信号周期的整数倍、采样率(Sampling Rate)必须高于信号最高频率的两倍以上、取样点数N必须为2k个数据。
快速傅里叶变换原理的表示法,则如下所示:

举例来说,当切换频率(fsw)为1050kHz的降压电路,输入电压为Vin=3.3伏特(V),Vo=1.8伏特,L=2.7微亨 (μH),Co=10微法(μF),ESR=4毫奥姆(mΩ),ESL=1.1奈亨(nH),fsw=280kHz。其实际量测的输出电压纹波、LX及电感纹波电流如图3所示。若给予任意输入波形,由傅里叶级数分析方法可得到对应的输出纹波,利用此方法提供一个快速有效的方式,可分析计算输入任意周期波的输出纹波。

图3 快速傅里叶变换vwin 波形与实际量测波形
应用时域分析输出纹波波形
时域分析是以时间函数(Time Function)表示信号之特性,依据时间及振幅所组成之坐标平面来呈现出任何信号波形随时间变化的瞬间物理量。时域分析输出电压纹波说明如下:

选择适当电感/电容值让设计优化
本文提供了傅里叶级数频域分析,其特色就是无须求解复杂的微分公式并与时域分析相对应,充分验证理论推导及实际量测波形的对比。目的是想以较严谨的输出电容等效电路来分析交换式降压转换器输出纹波电压。
经由上述论证可得知,电容的等效串联电阻、等效串联电感及电容值等特性均会影响输出纹波振幅及相位,并利用基本的奥姆定律、电感的微分公式推导电感与电流纹波变化,及电容器依据操作频率充/放电荷以维持输出电位稳定。
将上述三种影响纹波因素波形(等效串联电阻、等效串联电感及电容值)线性迭加,便可得到完整的输出纹波波形。透过此方法,可使研发工程师在设计切换式降压转换器电源时,根据电源需求及纹波允许变化量规格来选择适当的电感和电容值,使其设计达到优化。
责任编辑:gt
-
电源
+关注
关注
184文章
17704浏览量
249954 -
MOSFET
+关注
关注
147文章
7156浏览量
213133 -
晶体管
+关注
关注
77文章
9682浏览量
138077
发布评论请先 登录
相关推荐
小波与傅里叶分析基础





 通过傅里叶函数方法分析电源模块输出端纹波
通过傅里叶函数方法分析电源模块输出端纹波
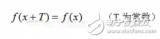










评论