引言
所谓的理想光学系统,就是对足够大空间内的各个点能以足够宽光束成完善像、理想像的光学系统。
1
理想光学系统
高斯光学(Gaussian optics)是指1841年C.高斯建立的研究理想光学系统的几何光学理论。它适用于任何结构的光学系统,但所研究的光线必须满足近轴条件。
所谓近轴条件,指的是光线与系统光轴的夹角α的正弦值可用角值(单位为弧度)代替,即sinα≈tanα≈α,cosα≈1。为便于一般地了解光学系统的成像性质和规律,在研究近轴区成像规律的基础上建立了理想光学系统的光学模型。
理想光学系统将物空间的同心宽光束转换到像空间的同心光束,这种从一个空间变换到另一个空间的情况,在数学上可以归结成“共线变换”或“共线成像”的问题,这种共轴理想光学系统理论是由高斯建立起来的,因此人们也把理想光学系统理论称为高斯光学。
2
物像关系的特性
1、点成点像:即对于物空间的每一点,在像空间必有一个点与之相对应,且只有一个点与之对应,这样的两个对应点称为物像空间的共轭点(如下图中的A点和A′点)。
2、线成线像:即对于物空间的每一条直线,在像空间必有一条直线与之相对应,且只有一条直线与之对应,这样的两条对应直线称为物像空间的共轭线(如下图中的BC和B′C′)。
3、平面成平面像:即物空间的每一个平面,在像空间必有一个平面与之相对应,且只有一个平面与之对应,这样的两个对应平面称为物像空间的共轭面(如下图中的PQ面和P′Q′面)。
由此推广,如果物空间上任意一点D位于直线BC上,那么其在像空间的共轭点D′也必位于共轭线B′C′上。同样,物空间中的一个同心光束必对应于像空间中的另一同心光束。上述这种点对点、直线对直线、平面对平面的成像,称为共线成像。
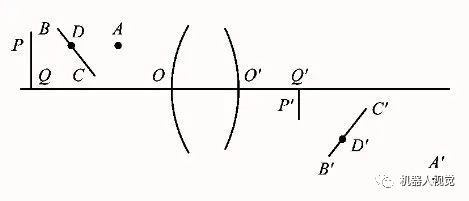
3
基点 基面
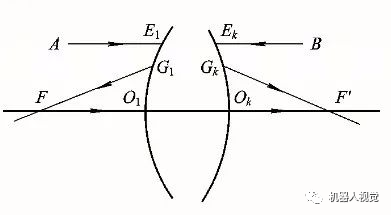
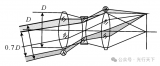
如下图所示,O1和Ok两点分别是理想光学系统第一面和最后一面的顶点,FO1OkF′为光轴。物空间的一条平行于光轴的直线AE1经光学系统折射后,其折射光线GkF′交光轴于F′点,另一条物方光线FO1与光轴重合,其折射光线OkF′无折射地仍沿光轴方向射出。
由于像方GkF′、OkF′分别与物方AE1、FO1相共轭,因此,交点F′为AE1和FO1交点(位于物方无穷远的光轴上)的共轭点,所以F′是物方无穷远轴上点的像,所有其它平行于光轴的入射光线均会聚于点F′,点F′称为光学系统的像方焦点(或称后焦点、第二焦点)。显然,像方焦点是物方无限远轴上点的共轭点。
基点 基面
同理,点F称为光学系统的物方焦点(或称前焦点、第一焦点),它与像方无穷远轴上点相共轭。任意一条过F点的入射光线经理想光学系统折射后,出射光线必平行于光轴。
通过像方焦点F′且垂直于光轴的平面,称为像方焦平面(像方焦面);通过物方焦点F且垂直于光轴的平面,称为物方焦平面(物方焦面)。
显然,像方焦平面的共轭面在无穷远处;同样,物方焦平面的共轭面也在无穷远处。像方焦平面上任何一个物点发出的光束,经理想光学系统出射后必为一平行光束;任何一束入射的平行光,经理想光学系统折射后,必会聚于像方焦平面上的某一点。
必须指出,焦点和焦面是理想光学系统的一对特殊的点和面。物方焦点F和像方焦点F′彼此之间不共轭,同样,物方焦平面和像方焦平面也不共轭。
如下图所示,O1和Ok两点分别是理想光学系统第一面和最后一面的顶点,FO1OkF′为光轴。物空间的一条平行于光轴的直线AE1经光学系统折射后,其折射光线GkF′交光轴于F′点,另一条物方光线FO1与光轴重合,其折射光线OkF′无折射地仍沿光轴方向射出。由于像方GkF′、OkF′分别与物方AE1、FO1相共轭,因此,交点F′为AE1和FO1交点(位于物方无穷远的光轴上)的共轭点,所以F′是物方无穷远轴上点的像,所有其它平行于光轴的入射光线均会聚于点F′,点F′称为光学系统的像方焦点(或称后焦点、第二焦点)。显然,像方焦点是物方无限远轴上点的共轭点。
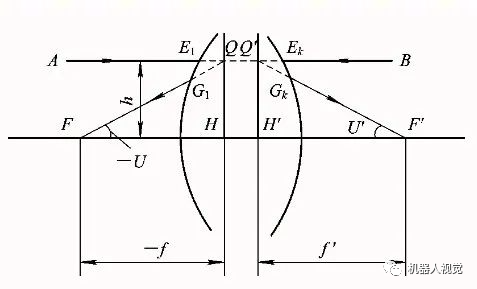
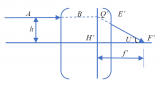
如下图所示,延长入射光线AE1和出射光线GkF′,得到交点Q′;同样,延长入射光线BEk和G1F,可得交点Q。
设光线AE1和BEk的入射高度相同,且都在子午面内。显然点Q和点Q′是一对共轭点。点Q是光线AE1和FQ交成的“虚物点”;点Q′是光线BEk和GkF′交成的“虚像点”。
过点Q和点Q′作垂直于光轴的平面QH和Q′H′,则这两个平面亦相互共轭。由图可知,位于这两个平面内的共轭线段QH和Q′H′具有相同的高度,且位于光轴的同一侧,故其垂轴放大率β =+1。我们称垂轴放大率为+1的这一对共轭面为主平面,其中的QH称为物方主平面(或前主面、第一主面),Q′H′称为像方主平面(或后主面、第二主面)。
物方主平面QH与光轴的交点H称为物方主点,像方主平面Q′H′与光轴的交点H′称为像方主点。
基点 基面
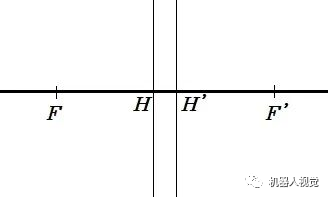
一对主点和一对焦点构成了光学系统的基点,一对主面和一对焦面构成了光学系统的基面,它们构成了一个光学系统的基本模型(下图所示)。
对于理想光学系统,不管其结构(r,d,n)如何,只要知道其焦距值和焦点或主点的位置,其性质就确定了。
参考文献:
【1】施特格。 机器视觉算法与应用[M]。 清华大学出版社, 2008.
【2】理想光学系统。百度百科
【3】工程光学(六)——几何光学(进阶).Tyalmath 。知乎
编辑:jq
-
光学系统
+关注
关注
4文章
243浏览量
18298
原文标题:【视觉知识】高斯光学,理想的光学系统
文章出处:【微信号:vision263com,微信公众号:新机器视觉】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
高倍金相自动测量显微镜无限远光学系统

高质量激光光束光学系统中的空间滤波
工业镜头光学系统的成像质量客观评价
如何检测光学系统的纵向色差
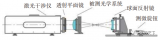
知语云智能科技揭秘:光学干扰技术全景解读
光学设计中的杂散光
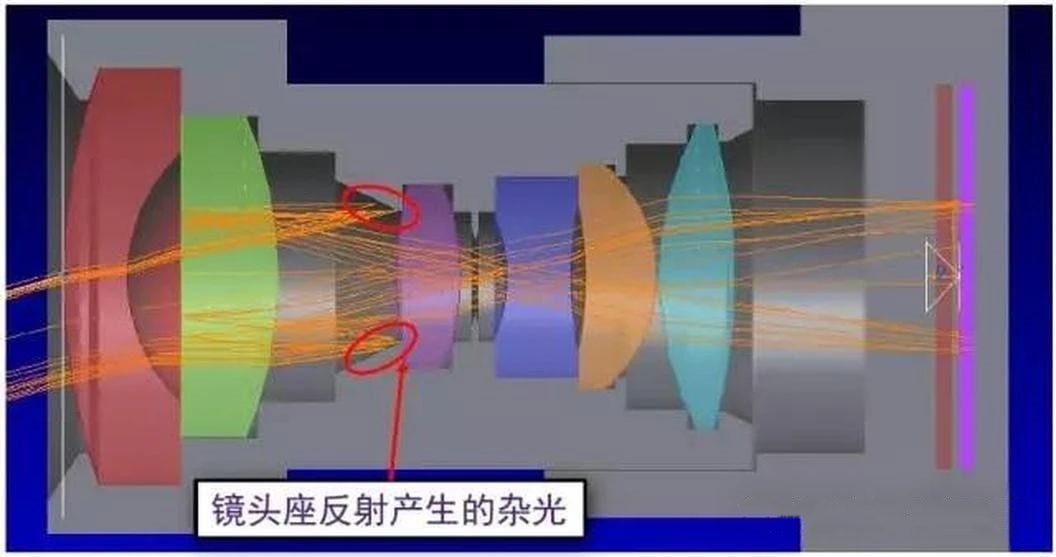
光学系统无热化技术的三个大类
光学设计的常用软件有哪些及其特点?
双波段CCTV鱼眼镜头光学系统设计
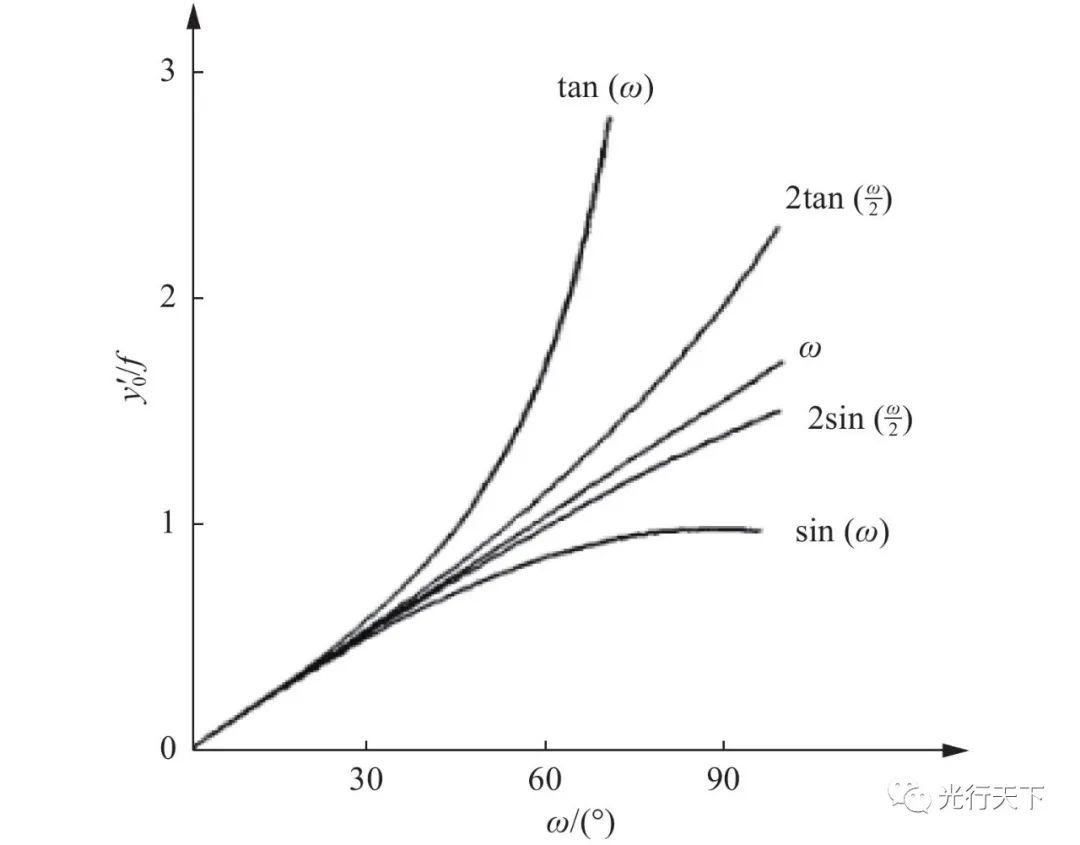




 高斯光学,理想的光学系统
高斯光学,理想的光学系统











评论