SPICE滞后建模的解决办法-德赢Vwin官网网

本文提供了一种构建标准 SPICE 模型的技术，该模型能够对具有连续滞后的系统的基本特征进行建模。

本文中的示例模型显示了向音频信号添加高频正弦波偏置以减少vwin 磁带录音机上的信号失真。该技术允许足够精确的近似值，说明滞后产生的失真以及如何通过添加高频偏置来减少它。

滞后模型

建模滞后的本质问题是它是具有记忆的静态或直流效应。也就是说，下一个值不仅取决于当前值，还取决于上一个值。然而，这个最后的值依赖不依赖于时间。这导致多值传递函数。

不幸的是，标准 SPICE 并不直接支持这种类型的建模。对 SPICE 中最后一个值的所有依赖通常是线性积分的结果，它固有地导致频率相关的传递函数，并且没有考虑失真机制。

解决这个问题的一种方法是简单地认识到一个人可以作弊。模拟模型只需要在有限的频率范围内大约做他们需要做的事情。分析表明，与非线性二极管电阻相结合的小电容器可用于在信号改变斜率方向以提供有效滞后之前连续存储信号的最后一个值，但不会过度依赖频率。

这与一些 SPICE“滞后”模型形成对比，这些模型只有两个输出状态模型，不允许连续传递函数。

线性模型

以下示意图构成了可用于建模的连续滞后模型的基础；例如，磁芯。

请注意，这里的输出电压是多值的，但本质上是线性超出死区的。当信号改变方向时会产生死区。它可以通过二极管参数 N 进行调整。

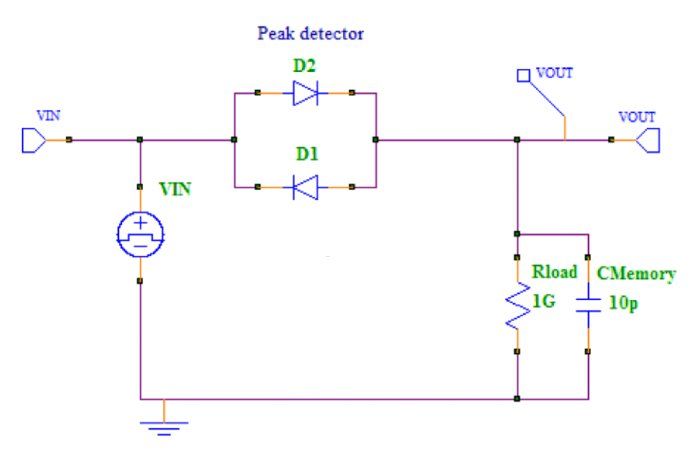
图 1. 连续滞后模型示意图

该模块的输出电压基本上线性跟随输入，但带有偏移电压。当输入反转时，电容器保持电压，使得从达到的峰值电压开始存在死区。

工作的关键原理是存在非线性阻抗，该阻抗在正向和反向偏置条件下具有急剧的电阻比。标准二极管方程是最简单的，但不是该技术的必要方程。这里用它来说明方法。

替代方程可用于微调响应特性。输入电压也可以进一步处理以获得不同的非线性传递曲线。此处的示例使用二极管的行为模型：

b1 aci={is}*（exp（{k}*v（a，c）） - 1）

为了获得准确的模型，选择组件的值，以便在希望对系统进行建模的频率范围内使频率影响最小化。

R load和 C memory的时间常数应使转弯前的最后一个电压不会泄漏太多。通过驱动阻抗（即在这种特殊情况下为二极管）的充电电流不会限制系统在所需工作频率范围内的响应。

对于各种输入电压和频率，上述拓扑产生以下一组传递函数和滞后图：

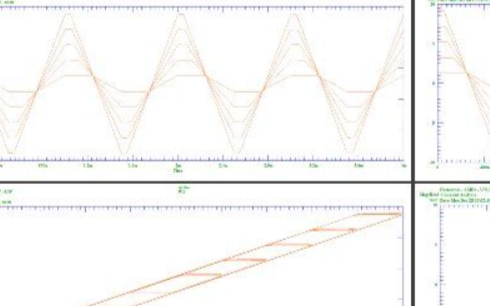
图 2. 斜坡输入传递函数 - F=1KHz， VIN=2V， 4V， 6V， 8V， 10V

图 3.斜坡输入传递函数 - F=1MHz， VIN=2V， 4V， 6V， 8V， 10V

图 4. 迟滞 - F=1kHz， VIN=2V， 4V， 6V， 8V， 10V

图 5. 迟滞 - F=1MHz， VIN=2V， 4V， 6V， 8V， 10V

图表的关键点是，在 1000:1 的频率范围内，电压传递函数和磁滞电压相对恒定，因此可以很好地逼近真实的直流磁滞。

通常，人们从具有所需正向和反向特性的受控电流源构建 SPICE 行为电阻。例如，正如我们上面指出的，滞后死区电压可以通过改变二极管参数“N”的默认值“1”来调整。

声明：本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人，不代表德赢Vwin官网网立场。文章及其配图仅供工程师学习之用，如有内容侵权或者其他违规问题，请联系本站处理。举报投诉

SPICE滞后建模的解决办法