二叉树的最大深度
尽管之前你可能做过这道题目，但只要认真看完，相信你会收获满满！可以一起解决如下两道题目：
- 104.二叉树的最大深度
- 559.n叉树的最大深度
104.二叉树的最大深度
题目地址：https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/
给定一个二叉树，找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例：给定二叉树 [3,9,20,null,null,15,7]，
返回它的最大深度 3 。
递归法
本题可以使用前序（中左右），也可以使用后序遍历（左右中），使用前序求的就是深度，使用后序求的是高度。
而根节点的高度就是二叉树的最大深度，所以本题中我们通过后序求的根节点高度来求的二叉树最大深度。
这一点其实是很多同学没有想清楚的，很多题解同样没有讲清楚。
我先用后序遍历（左右中）来计算树的高度。
- 确定递归函数的参数和返回值：参数就是传入树的根节点，返回就返回这棵树的深度，所以返回值为int类型。
代码如下：
intgetdepth(treenode*node)
- 确定终止条件：如果为空节点的话，就返回0，表示高度为0。
代码如下：
if(node==null)return0;
- 确定单层递归的逻辑：先求它的左子树的深度，再求的右子树的深度，最后取左右深度最大的数值 再+1 （加1是因为算上当前中间节点）就是目前节点为根节点的树的深度。
代码如下：
intleftdepth=getdepth(node->left);//左
intrightdepth=getdepth(node->right);//右
intdepth=1+max(leftdepth,rightdepth);//中
returndepth;
所以整体c++代码如下：
classsolution{
public:
intgetdepth(treenode*node){
if(node==null)return0;
intleftdepth=getdepth(node->left);//左
intrightdepth=getdepth(node->right);//右
intdepth=1+max(leftdepth,rightdepth);//中
returndepth;
}
intmaxdepth(treenode*root){
returngetdepth(root);
}
};
代码精简之后c++代码如下：
classsolution{
public:
intmaxdepth(treenode*root){
if(root==null)return0;
return1+max(maxdepth(root->left),maxdepth(root->right));
}
};
精简之后的代码根本看不出是哪种遍历方式，也看不出递归三部曲的步骤，所以如果对二叉树的操作还不熟练，尽量不要直接照着精简代码来学。
本题当然也可以使用前序，代码如下：(充分表现出求深度回溯的过程)
classsolution{
public:
intresult;
voidgetdepth(treenode*node,intdepth){
result=depth>result?depth:result;//中
if(node->left==null&&node->right==null)return;
if(node->left){//左
depth++;//深度+1
getdepth(node->left,depth);
depth--;//回溯，深度-1
}
if(node->right){//右
depth++;//深度+1
getdepth(node->right,depth);
depth--;//回溯，深度-1
}
return;
}
intmaxdepth(treenode*root){
result=0;
if(root==0)returnresult;
getdepth(root,1);
returnresult;
}
};
可以看出使用了前序（中左右）的遍历顺序，这才是真正求深度的逻辑！
注意以上代码是为了把细节体现出来，简化一下代码如下：
classsolution{
public:
intresult;
voidgetdepth(treenode*node,intdepth){
result=depth>result?depth:result;//中
if(node->left==null&&node->right==null)return;
if(node->left){//左
getdepth(node->left,depth+1);
}
if(node->right){//右
getdepth(node->right,depth+1);
}
return;
}
intmaxdepth(treenode*root){
result=0;
if(root==0)returnresult;
getdepth(root,1);
returnresult;
}
};
迭代法
使用迭代法的话，使用层序遍历是最为合适的，因为最大的深度就是二叉树的层数，和层序遍历的方式极其吻合。
在二叉树中，一层一层的来遍历二叉树，记录一下遍历的层数就是二叉树的深度，如图所示：
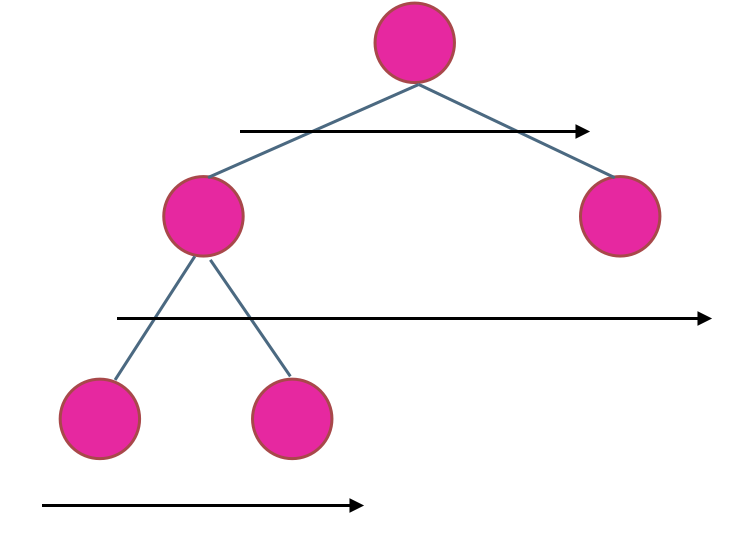
所以这道题的迭代法就是一道模板题，可以使用二叉树层序遍历的模板来解决的。
如果对层序遍历还不清楚的话，可以看这篇：二叉树：层序遍历登场！
c++代码如下：
classsolution{
public:
intmaxdepth(treenode*root){
if(root==null)return0;
intdepth=0;
queueque;
que.push(root);
while(!que.empty()){
intsize=que.size();
depth++;//记录深度
for(inti=0;i< size; i++) {
treenode* node = que.front();
que.pop();
if(node->left)que.push(node->left);
if(node->right)que.push(node->right);
}
}
returndepth;
}
};
那么我们可以顺便解决一下n叉树的最大深度问题
559.n叉树的最大深度
题目地址：https://leetcode-cn.com/problems/maximum-depth-of-n-ary-tree/
给定一个 n 叉树，找到其最大深度。
最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。
例如，给定一个 3叉树 :
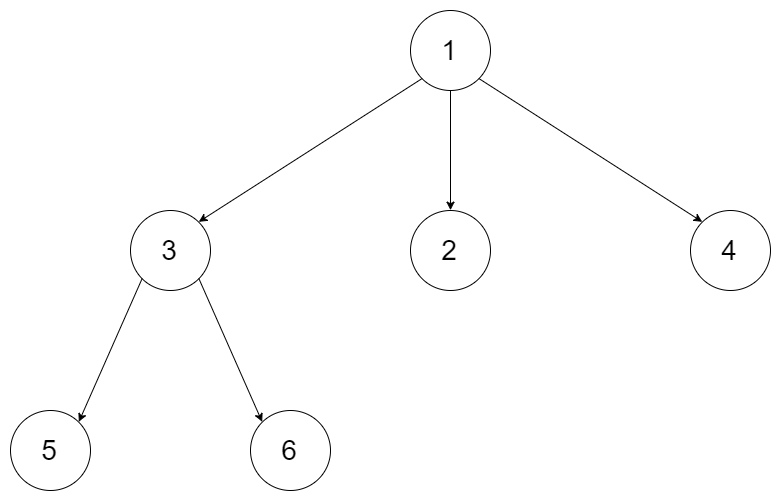
我们应返回其最大深度，3。
思路：
依然可以提供递归法和迭代法，来解决这个问题，思路是和二叉树思路一样的，直接给出代码如下：
递归法
c++代码：
classsolution{
public:
intmaxdepth(node*root){
if(root==0)return0;
intdepth=0;
for(inti=0;i< root->children.size();i++){
depth=max(depth,maxdepth(root->children[i]));
}
returndepth+1;
}
};
迭代法
依然是层序遍历，代码如下：
classsolution{
public:
intmaxdepth(node*root){
queueque;
if(root!=null)que.push(root);
intdepth=0;
while(!que.empty()){
intsize=que.size();
depth++;//记录深度
for(inti=0;i< size; i++) {
node* node = que.front();
que.pop();
for(intj=0;j< node->children.size();j++){
if(node->children[j])que.push(node->children[j]);
}
}
}
returndepth;
}
};
其他语言版本
java
104.二叉树的最大深度
classsolution{
/**
*递归法
*/
publicintmaxdepth(treenoderoot){
if(root==null){
return0;
}
intleftdepth=maxdepth(root.left);
intrightdepth=maxdepth(root.right);
returnmath.max(leftdepth,rightdepth)+1;
}
}
classsolution{
/**
*迭代法，使用层序遍历
*/
publicintmaxdepth(treenoderoot){
if(root==null){
return0;
}
dequedeque=newlinkedlist<>();
deque.offer(root);
intdepth=0;
while(!deque.isempty()){
intsize=deque.size();
depth++;
for(inti=0;i< size; i++) {
treenode poll = deque.poll();
if(poll.left!=null){
deque.offer(poll.left);
}
if(poll.right!=null){
deque.offer(poll.right);
}
}
}
returndepth;
}
}
python
104.二叉树的最大深度
递归法：
classsolution:
defmaxdepth(self,root:treenode)->int:
returnself.getdepth(root)
defgetdepth(self,node):
ifnotnode:
return0
leftdepth=self.getdepth(node.left)#左
rightdepth=self.getdepth(node.right)#右
depth=1+max(leftdepth,rightdepth)#中
returndepth
递归法：精简代码
classsolution:
defmaxdepth(self,root:treenode)->int:
ifnotroot:
return0
return1+max(self.maxdepth(root.left),self.maxdepth(root.right))
迭代法：
importcollections
classsolution:
defmaxdepth(self,root:treenode)->int:
ifnotroot:
return0
depth=0#记录深度
queue=collections.deque()
queue.append(root)
whilequeue:
size=len(queue)
depth+=1
foriinrange(size):
node=queue.popleft()
ifnode.left:
queue.append(node.left)
ifnode.right:
queue.append(node.right)
returndepth
559.n叉树的最大深度
递归法：
classsolution:
defmaxdepth(self,root:'node')->int:
ifnotroot:
return0
depth=0
foriinrange(len(root.children)):
depth=max(depth,self.maxdepth(root.children[i]))
returndepth+1
迭代法：
importcollections
classsolution:
defmaxdepth(self,root:'node')->int:
queue=collections.deque()
ifroot:
queue.append(root)
depth=0#记录深度
whilequeue:
size=len(queue)
depth+=1
foriinrange(size):
node=queue.popleft()
forjinrange(len(node.children)):
ifnode.children[j]:
queue.append(node.children[j])
returndepth
使用栈来vwin 后序遍历依然可以
classsolution:
defmaxdepth(self,root:'node')->int:
st=[]
ifroot:
st.append(root)
depth=0
result=0
whilest:
node=st.pop()
ifnode!=none:
st.append(node)#中
st.append(none)
depth+=1
foriinrange(len(node.children)):#处理孩子
ifnode.children[i]:
st.append(node.children[i])
else:
node=st.pop()
depth-=1
result=max(result,depth)
returnresult
审核编辑 ：李倩
声明：本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人，不代表德赢Vwin官网
网立场。文章及其配图仅供工程师学习之用，如有内容侵权或者其他违规问题，请联系本站处理。
举报投诉
-
C++
+关注
关注
22文章
2108浏览量
73616 -
代码
+关注
关注
30文章
4779浏览量
68516 -
二叉树
+关注
关注
0文章
74浏览量
12324
原文标题：看看这些树的最大深度！
文章出处：【微信号：TheAlgorithm，微信公众号：算法与数据结构】欢迎添加关注！文章转载请注明出处。
发布评论请先 登录
相关推荐
GPU深度学习应用案例
能力，可以显著提高图像识别模型的训练速度和准确性。例如，在人脸识别、自动驾驶等领域，GPU被广泛应用于加速深度学习模型的训练和推理过程。 二、自然语言处理 自然语言处理（NLP）是深度学习的另一个重要应用领域。GPU可以加速NL
镭神智能机器人三向叉式3D SLAM无人叉车：重塑高位堆垛与窄通道仓储新境界
在智能制造与智慧物流的浪潮中，镭神智能凭借其卓越的技术实力，推出了革命性的三向叉式3DSLAM无人叉车LXK12-B。这款无人叉车不仅集成了自主搬运、智能堆垛等功能，更以举升高度5m、货叉180
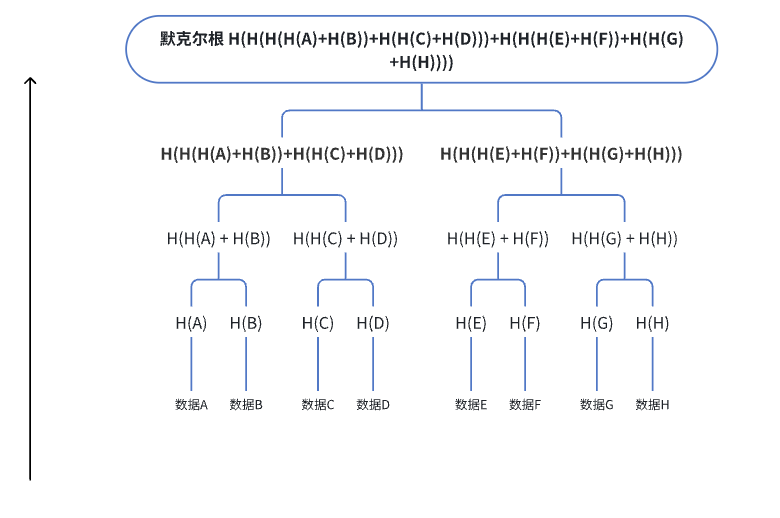
什么是默克尔树(Merkle Tree)？如何计算默克尔根?
01 默克尔树的概念 默克尔树(Merkle Tree)是一种特殊的二叉树，它的每个节点都存储了一个数据块的哈希值。哈希值是一种可以将任意长度的数据转换为固定长度的字符串的算法，它具有唯一性和不可
二极管击穿电压是最大值还是有效值
二极管击穿电压是指二极管在反向偏置下，电流突然增大，导致二极管损坏的电压值。 最大值（Peak Value）：最大值是指在一个周期内，电压或
二极管的最大整流电流是什么
二极管是一种半导体器件，其主要功能是允许电流单向流动。在电子电路中，二极管被广泛应用于整流、稳压、开关等场合。二极管的最大整流电流是指在保证二
影响二极管最大整流电流的因素
二极管是一种半导体器件，广泛应用于电子电路中，其主要功能是实现单向导电。在实际应用中，二极管的整流能力是非常重要的一个参数，它直接影响到电路的稳定性和可靠性。 一、二极管最大整流电流的
多叉指MOSFET器件静电防护鲁棒性提升技巧
栅极接地NMOS是一种广泛应用的片上ESD器件结构，为达到特定ESD防护等级，一般会采用多叉指版图形式来减小器件占用的芯片面积。但是，多叉指栅极接地NMOS在ESD应力作用下，各个叉指难于做到均匀
原理图设计里两颗重要的树（国产EDA）
原理图里面两颗重要的树，那就是元件树和网络树，作为EDA工具中的重要视图和概念，虽然看似枯燥，但它们扮演着非常重要的角色，它们为电路图的层次化结构提供了有力支撑。想象一个大型的电路设计项目，就像一个
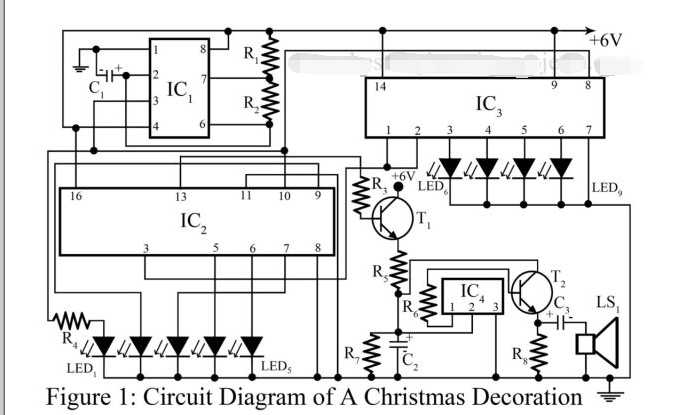
圣诞树灯电路图分享
圣诞装饰的电路分为两个主要部分，即灯光和声音部分。照明部分由五组 LED 组成，它们以二进制顺序运行，每隔几分钟就会重复一次。在这里，根据我们的兴趣，LED 可以是任何颜色。这件装饰品可以装饰您的圣诞树以及您的家。
迅镭激光中标叉车行业龙头杭叉集团！
中国制造业企业500强、中国民营企业500强——杭叉集团响应号召，更“新”设备，引入迅镭高功率激光切割设备，建设智能工厂，向世界展示中国制造的智慧与力量！
华睿科技近期推出新一代堆高式叉取型AMR FD150
华睿科技近期推出新一代堆高式叉取型AMR FD150。FD150基于AMR专用车身设计，额定负载1500KG，最大举升高度2m，满足最小2.2m通道内自主识别取放货。
哈夫曼编码怎么算 哈夫曼编码左边是0还是1
二叉树，将出现频率高的字符用较短的编码表示，而出现频率低的字符则用较长的编码表示。通过这种方式，可以实现对数据进行高效的编码和解码。 下面我们将详细介绍哈夫曼编码的算法过程。 统计字符频率 在进行哈夫曼编码前，首先需
MCP251X can驱动移植nuc980采样用设备树配置时，中断如何配置设备树?
MCP251X can驱动移植nuc980 采样用设备树配置时，中断如何配置设备树?
spi0: spi@b0061000 {
status = \"okay\"
发表于 01-17 06:43
工商网监
评论