抽样在Python中是如何实现的
今天来和大家聊聊抽样的几种常用方法，以及在Python中是如何实现的。 抽样是统计学、机器学习中非常重要，也是经常用到的方法，因为大多时候使用全量数据是不现实的，或者根本无法取到。所以我们需要抽样，比如在推断性统计中，我们会经常通过采样的样本数据来推断估计总体的样本。 上面所说的都是以概率为基础的，实际上还有一类非概率的抽样方法，因此总体上归纳为两大种类：
概率抽样：根据概率理论选择样本，每个样本有相同的概率被选中。
非概率抽样：根据非随机的标准选择样本，并不是每个样本都有机会被选中。
概率抽样技术
1.随机抽样(Random Sampling)
这也是最简单暴力的一种抽样了，就是直接随机抽取，不考虑任何因素，完全看概率。并且在随机抽样下，总体中的每条样本被选中的概率相等。 
比如，现有10000条样本，且各自有序号对应的，假如抽样数量为1000，那我就直接从1-10000的数字中随机抽取1000个，被选中序号所对应的样本就被选出来了。 在Python中，我们可以用random函数随机生成数字。下面就是从100个人中随机选出5个。
importrandom population=100 data=range(population) print(random.sample(data,5)) >4,19,82,45,41
2.分层抽样(Stratified Sampling)
分层抽样其实也是随机抽取，不过要加上一个前提条件了。在分层抽样下，会根据一些共同属性将带抽样样本分组，然后从这些分组中单独再随机抽样。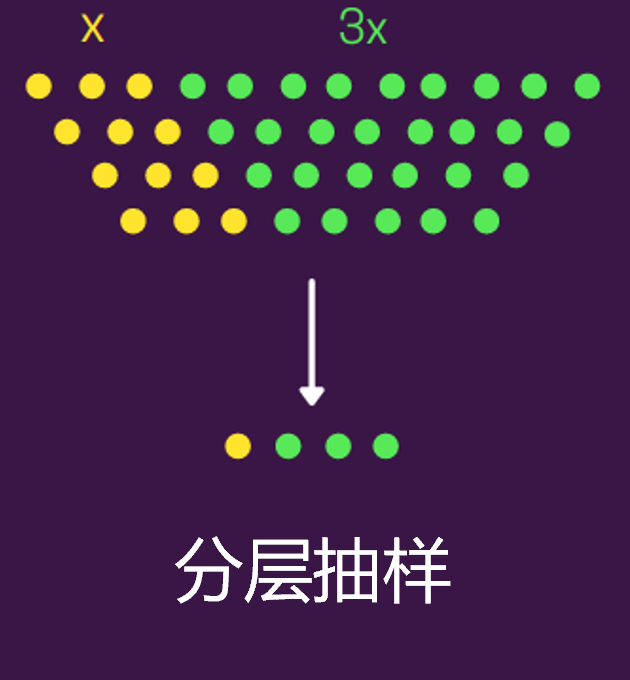 
因此，可以说分层抽样是更精细化的随机抽样，它要保持与总体群体中相同的比例。 比如，机器学习分类标签中的类标签0和1，比例为3:7，为保持原有比例，那就可以分层抽样，按照每个分组单独随机抽样。 Python中我们通过train_test_split设置stratify参数即可完成分层操作。
fromsklearn.model_selectionimporttrain_test_split stratified_sample,_=train_test_split(population,test_size=0.9,stratify=population[['label']]) print(stratified_sample)
3.聚类抽样(Cluster Sampling)
聚类抽样，也叫整群抽样。它的意思是，先将整个总体划分为多个子群体，这些子群体中的每一个都具有与总体相似的特征。也就是说它不对个体进行抽样，而是随机选择整个子群体。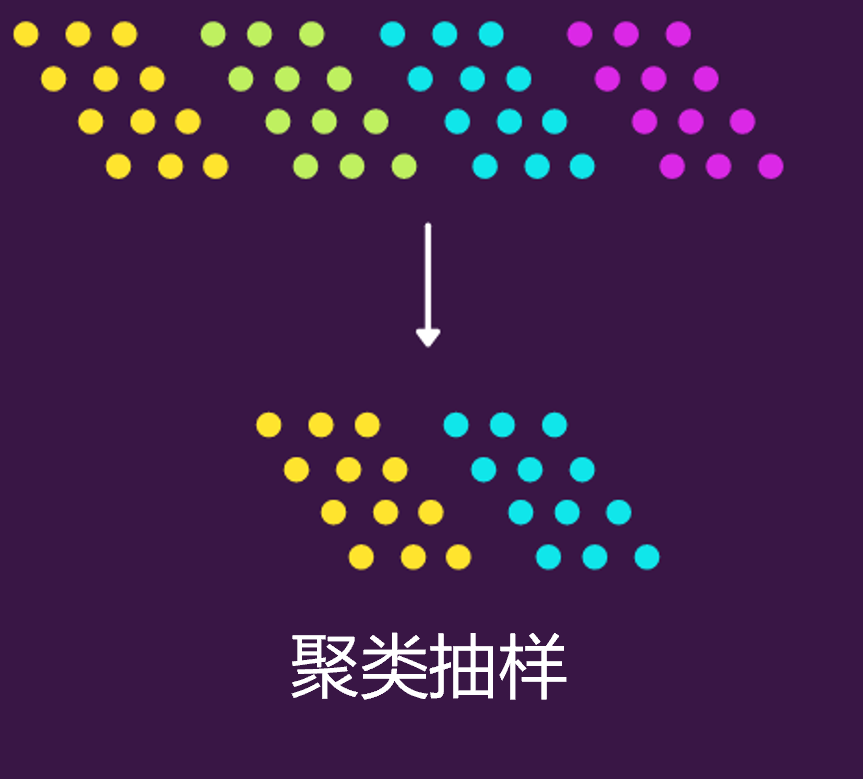 
用Python可以先给聚类的群体分配聚类ID，然后随机抽取两个子群体，再找到相对应的样本值即可，如下。
importnumpyasnp clusters=5 pop_size=100 sample_clusters=2 #间隔为20,从1到5依次分配集群100个样本的聚类ID，这一步已经假设聚类完成 cluster_ids=np.repeat([range(1,clusters+1)],pop_size/clusters) #随机选出两个聚类的ID cluster_to_select=random.sample(set(cluster_ids),sample_clusters) #提取聚类ID对应的样本 indexes=[ifori,xinenumerate(cluster_ids)ifxincluster_to_select] #提取样本序号对应的样本值 cluster_associated_elements=[elforidx,elinenumerate(range(1,101))ifidxinindexes] print(cluster_associated_elements)
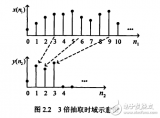
4.系统抽样(Systematic Sampling)
系统抽样是以预定的规则间隔（基本上是固定的和周期性的间隔）从总体中抽样。比如，每 9 个元素抽取一下。一般来说，这种抽样方法往往比普通随机抽样方法更有效。 下图是按顺序对每 9 个元素进行一次采样，然后重复下去。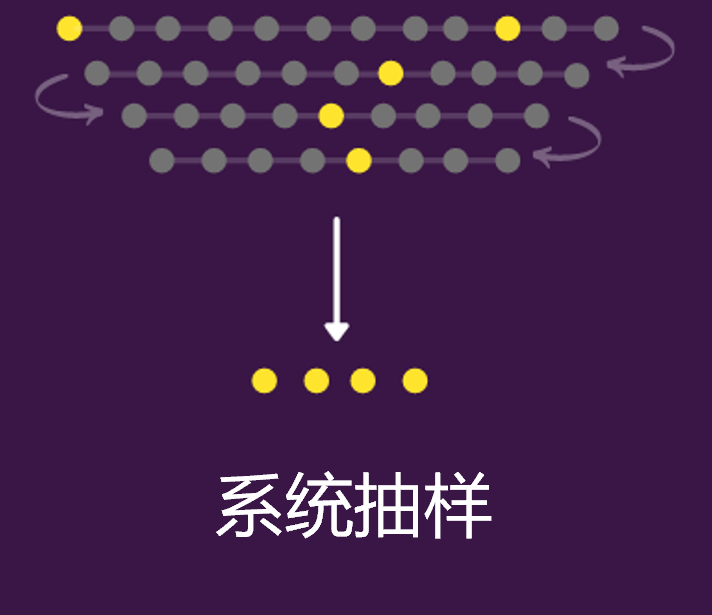 
用Python实现的话可以直接在循环体中设置step即可。
population=100 step=5 sample=[elementforelementinrange(1,population,step)] print(sample)
5.多级采样(Multistage sampling)
在多阶段采样下，我们将多个采样方法一个接一个地连接在一起。比如，在第一阶段，可以使用聚类抽样从总体中选择集群，然后第二阶段再进行随机抽样，从每个集群中选择元素以形成最终集合。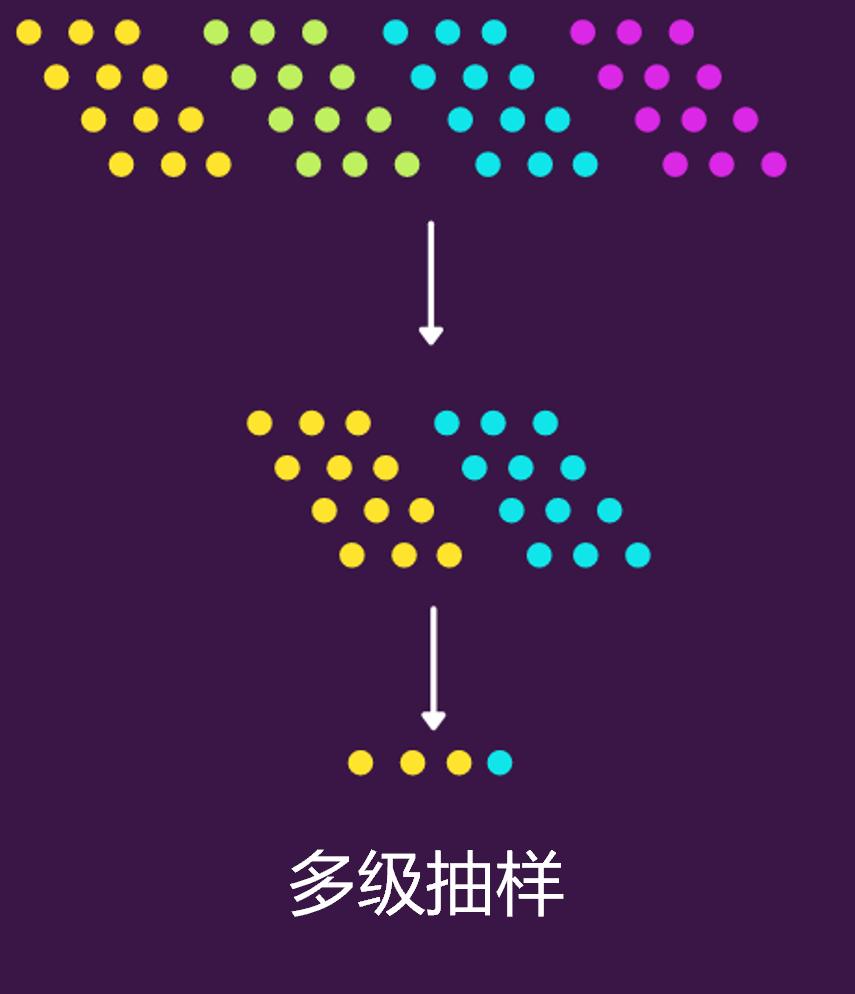 
Python代码复用了上面聚类抽样，只是在最后一步再进行随机抽样即可。
importnumpyasnp clusters=5 pop_size=100 sample_clusters=2 sample_size=5 #间隔为20,从1到5依次分配集群100个样本的聚类ID，这一步已经假设聚类完成 cluster_ids=np.repeat([range(1,clusters+1)],pop_size/clusters) #随机选出两个聚类的ID cluster_to_select=random.sample(set(cluster_ids),sample_clusters) #提取聚类ID对应的样本 indexes=[ifori,xinenumerate(cluster_ids)ifxincluster_to_select] #提取样本序号对应的样本值 cluster_associated_elements=[elforidx,elinenumerate(range(1,101))ifidxinindexes] #再从聚类样本里随机抽取样本 print(random.sample(cluster_associated_elements,sample_size))
非概率抽样技术
非概率抽样，毫无疑问就是不考虑概率的方式了，很多情况下是有条件的选择。因此，对于无随机性我们是无法通过统计概率和编程来实现的。这里也介绍3种方法。
1.简单采样(convenience sampling)
简单采样，其实就是研究人员只选择最容易参与和最有机会参与研究的个体。比如下面的图中，蓝点是研究人员，橙色点则是蓝色点附近最容易接近的人群。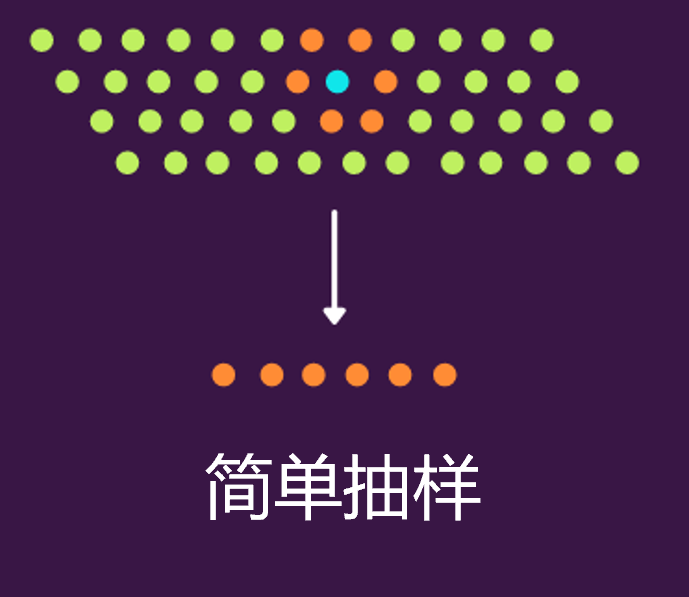 
2.自愿抽样(Voluntary Sampling)
自愿抽样下，感兴趣的人通常通过填写某种调查表格形式自行参与的。所以，这种情况中，调查的研究人员是没有权利选择任何个体的，全凭群体的自愿报名。比如下图中蓝点是研究人员，橙色的是自愿同意参与研究的个体。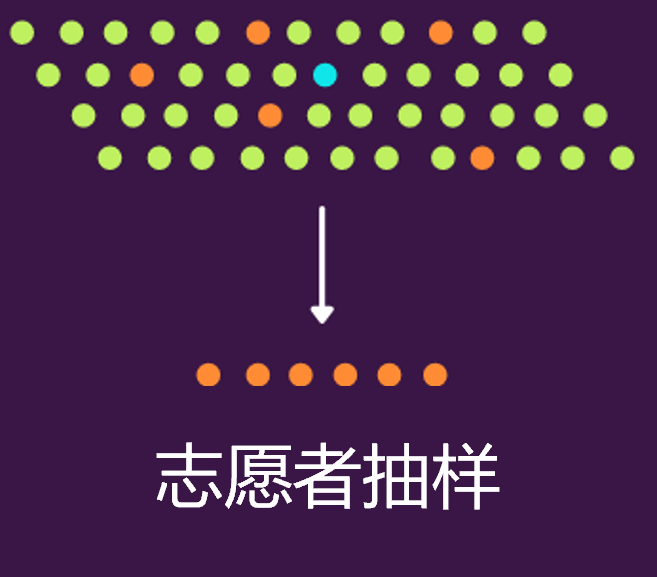 
3.雪球抽样(Snowball Sampling)
雪球抽样是说，最终集合是通过其他参与者选择的，即研究人员要求其他已知联系人寻找愿意参与研究的人。比如下图中蓝点是研究人员，橙色的是已知联系人，黄色是是橙色点周围的其它联系人。
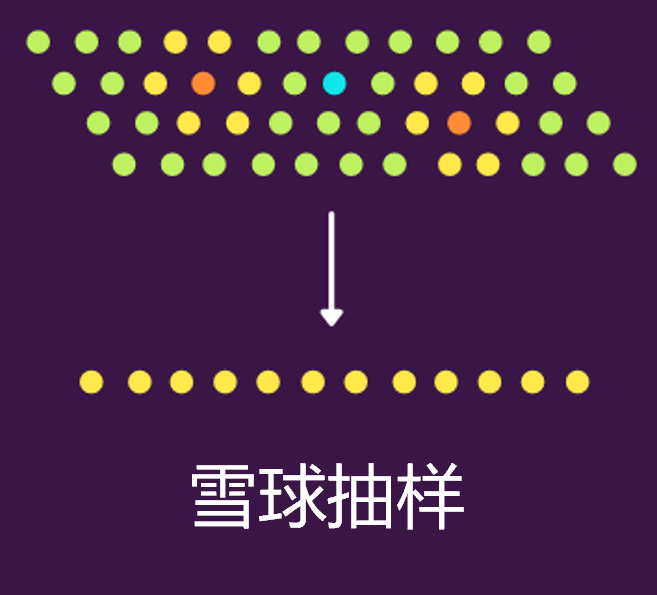
总结
以上就是8种常用抽样方法，平时工作中比较常用的还是概率类抽样方法，因为没有随机性我们是无法通过统计学和编程完成自动化操作的。
比如在信贷的风控样本设计时，就需要从样本窗口通过概率进行抽样。因为采样的质量基本就决定了你模型的上限了，所以在抽样时会考虑很多问题，如样本数量、是否有显著性、样本穿越等等。在这时，一个良好的抽样方法是至关重要的。
-
抽样
+关注
关注
0文章
11浏览量
7152 -
机器学习
+关注
关注
66文章
8406浏览量
132557 -
python
+关注
关注
56文章
4792浏览量
84624
原文标题：基于 Python 的 8 种常用抽样方法
文章出处：【微信号：AI科技大本营，微信公众号：AI科技大本营】欢迎添加关注！文章转载请注明出处。
发布评论请先 登录
相关推荐
怎样实现中频窄带抽样？
通信原理抽样定理及应用实验报告
抽样z变换频率抽样理论
信号抽样与抽样定理.ppt
多抽样率原理在舰船振动信号分析中的应用与研究
基于Dijkstra最短路径的抽样算法
在Anaconda中安装python包seaborn
工商网监
评论