一阶数字低通滤波器原理及公式推导
前面我们基本把有感FOC介绍得差不多了，接下来我本打算进入无感FOC控制的深入学习，奈何导师项目项目太多太杂........................先把自己这段时间学的东西总结分享一下再说吧。查阅了很多无感FOC控制的相关资料，把基本原理和流程渐渐的了解了一下（以后有时间再详细介绍了），发现很多环节都会用到”一阶低通数字滤波器“（相电流滤波，反电势滤波，角度、转速滤波，校正因子滤波），虽然代码里面只是一个简单的公式，但为了控制系统的参数设计，我还是浅浅的去探究了一下其基本原理，如有错误还望提出指正。
开局先直接给出公式：
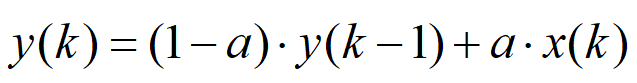
式中：x(k)为当前输入，y(k-1)为上一次的输出，y(k)为当前计算的输出；a为滤波系数，取值范围0~1，a取值越小，当前输入权重就越小，输出波形越平滑，但响应灵敏度降低；
如果只是套用公式写代码的话，看到这里就可以结束了，想要理解其中的原理，以及采样频率、截止频率和参数的计算，那么请接着往下看。
01. 原理及公式推导
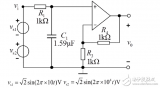
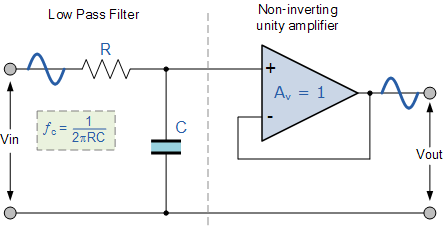
”一阶低通数字滤波器“对应的物理电路模型是”一阶RC低通滤波电路“，电路如下图所示。
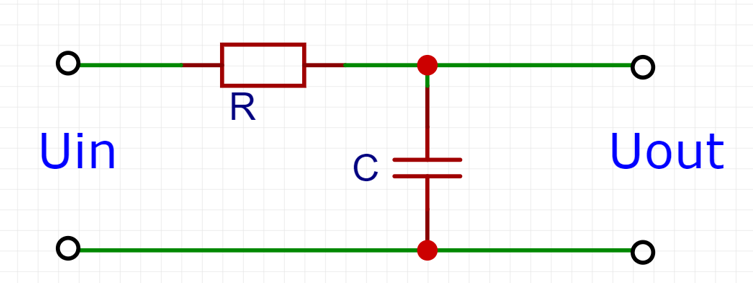
电容的阻抗表示为1/jωC，对于上面电路，有输入输出电压关系：
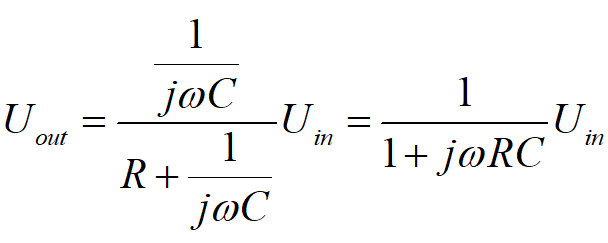
上式写成传递函数形式：
，
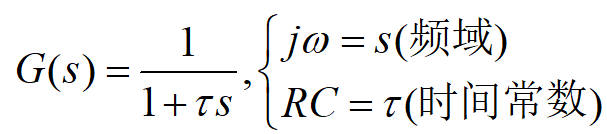在《自动控制原理》中称为一阶惯性环节。
由Y(s)=G(s).F(s)得到时域的微分方程：
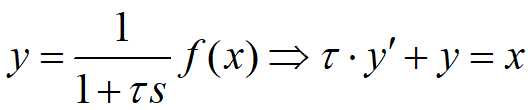
使用一阶后向差分法，对上面微分方程进行离散化，有：
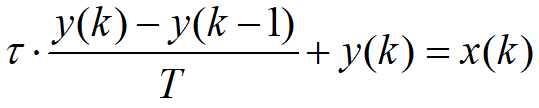
其中T为采样周期，对上式进行整理化简可写成：
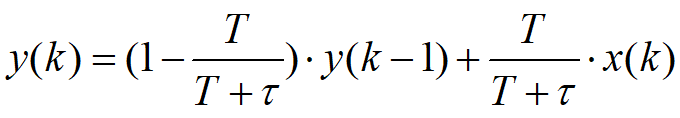
令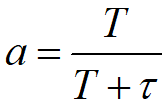
得到一般表达式：
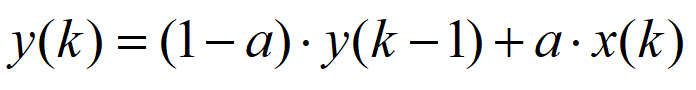，a称为滤波系数。
02. 截止频率和参数计算
对于电路模型，有截止频率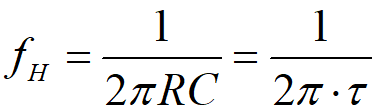
（截止频率定义为幅频响应曲线衰减 -3db，即为原来的1/sqrt(2)时的频率，模电里面的基础知识这里不细讲）
可得是将常数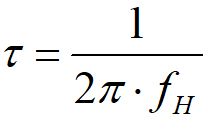
代入滤波系数a的表达式得：
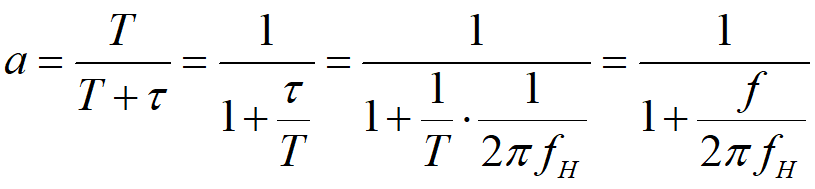
式中f=1/T为采样频率。
在实际的应用中，一般有采样频率远大于截止频率，即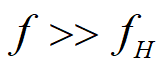有
，故近似有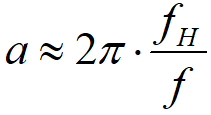
，所以已知截止频率和采样频率，我么就能够计算滤波系数a的值了。
又会问：截止频率和采样频率怎么确定呢？选取不同的值会对计算输出有什么影响呢？下面为你简单介绍一下。
03. 频率的选择
3.1采样频率的选择
一般人为主观选择，在不影响其他功能性能的条件下，尽量越大越好。
先以我之前做的电机控制为例。在程序中，PWM定时器开启中断，在中断服务函数中用ADC采集相电流，故采样频率就等于PWM定时器频率，我在控制代码中用的是20kHz，即采样频率f=20kHz。
3.2截止频率的选择
根据采样对象信号的频率选择，一般稍大于被采样信号的最大基波频率就好。
还是以我做的电机控制为例。我用的永磁同步电机额定转速为3000rpm，极对数为4，采样对象为相电流。则在额定条件下，相电流的频率为f_current=3000*4/60=200Hz，考虑到电机超负荷运行，瞬时转速可以大于3000，保留一定余量，我取截止频率f_H=500Hz。如此计算得滤波系数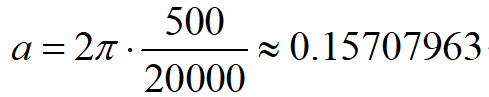
。
在电机运行前，对放大器进行校准时，只考虑直流偏置输入，即被采样的信号频率趋近于0Hz，主要滤掉电路中的高频干扰和噪声，故可把截止频率取得很小，我这里取f_H=5Hz，计算得滤波系数a=0.00157。
04频率选择对输出的影响（附仿真分析）
在采样频率固定的情况下，截止频率越大，滤波系数a的值越大，当前输入的权重就越大，计算的输出和实际的输出跟踪效果更好，即动态响应更好，幅值衰减的影响更小。
减小截止频率，滤波系数a的值越小，当前输入的权重越小，故计算的输出信号更平滑，对噪声干扰和谐波的滤除效果更好，但是动态响应变差，而且会产生一定程度的幅值衰减。
下面是matlab代码和仿真结果分析：
仿真结果：
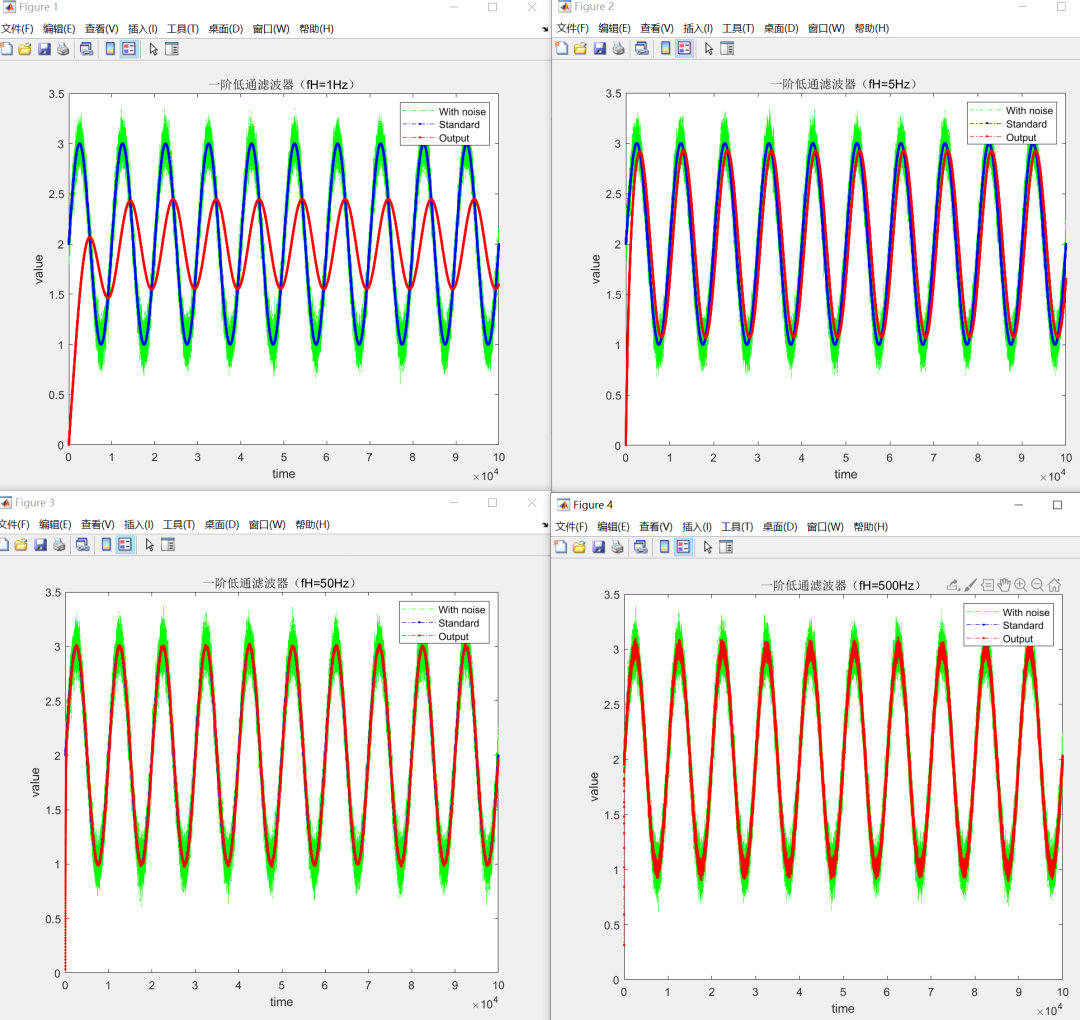
图中，绿色为含有噪声的采样信号，蓝色为标准的正弦信号，红色为采样信号经过一阶低通滤波器的计算输出。
可以发现，当截止频率较小时，输出信号幅值衰减明显，且存在一定滞后；随着截止频率的增大，对标准正弦信号的跟踪效果越好；当截止频率过大时，几乎能完全复现采样信号，但是对噪声的滤波效果变差。
下面再看一下对直流信号的测试
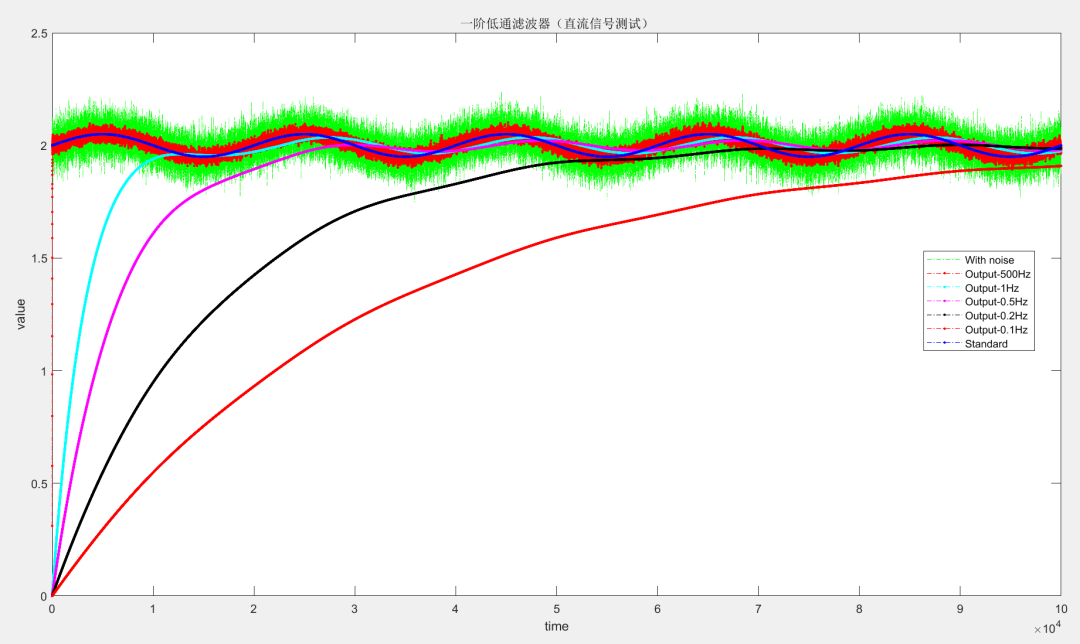
可以看出，随着截止频率的减小，计算输出的信号越来越平滑，接近直流信号，但同时调节时间也增大，对应我前面电机控制中，对放大器的校准时间需要延长。在实际应用中，对于直流信号的滤波，截止频率一般取1~50Hz我觉得就好了（当然也有可能其它情况我没想到）。
最后附上matlab的仿真源代码
代码源程序：
交流信号部分：
f_basic=200;%原信号频率为200Hzw_basic=2*pi*f_basic;f_H=1;%截止频率500Hzf_simple=20000;%采样频率20kHzPointNumber = 100000;%坐标点数量x=0PointNumber-1;Standard =2+sin(w_basic*x*0.0000005);%原始标准信号noise = 0+0.1*randn(1,PointNumber);AddNoise=Standard+noise;a=2*pi*f_H/f_simple;y_last=0;y_now=0;for i = 0PointNumber-1x_now=AddNoise(i+1);y_now=(1-a)*y_last+a*x_now;output(i+1)=y_now;y_last=y_now;endfigure(1);X=0PointNumber-1;plot(X,AddNoise,'-.g');hold on;plot(X,Standard,'-..b');hold on;plot(X,output,'-..r');hold on;legend('With noise','Standard','Output')xlabel('time');ylabel('value');title('一阶低通滤波器（fH=1Hz）');f_basic=200;%原信号频率为200Hzw_basic=2*pi*f_basic;f_H=5;%截止频率500Hzf_simple=20000;%采样频率20kHzPointNumber = 100000;%坐标点数量x=0PointNumber-1;Standard =2+sin(w_basic*x*0.0000005);%原始标准信号noise = 0+0.1*randn(1,PointNumber);AddNoise=Standard+noise;a=2*pi*f_H/f_simple;y_last=0;y_now=0;for i = 0PointNumber-1x_now=AddNoise(i+1);y_now=(1-a)*y_last+a*x_now;output(i+1)=y_now;y_last=y_now;endfigure(2);X=0PointNumber-1;plot(X,AddNoise,'-.g');hold on;plot(X,Standard,'-..b');hold on;plot(X,output,'-..r');hold on;legend('With noise','Standard','Output')xlabel('time');ylabel('value');title('一阶低通滤波器（fH=5Hz）');f_basic=200;%原信号频率为200Hzw_basic=2*pi*f_basic;f_H=50;%截止频率500Hzf_simple=20000;%采样频率20kHzPointNumber = 100000;%坐标点数量x=0PointNumber-1;Standard =2+sin(w_basic*x*0.0000005);%原始标准信号noise = 0+0.1*randn(1,PointNumber);AddNoise=Standard+noise;a=2*pi*f_H/f_simple;y_last=0;y_now=0;for i = 0PointNumber-1x_now=AddNoise(i+1);y_now=(1-a)*y_last+a*x_now;output(i+1)=y_now;y_last=y_now;endfigure(3);X=0PointNumber-1;plot(X,AddNoise,'-.g');hold on;plot(X,Standard,'-..b');hold on;plot(X,output,'-..r');hold on;legend('With noise','Standard','Output')xlabel('time');ylabel('value');title('一阶低通滤波器（fH=50Hz）');f_basic=200;%原信号频率为200Hzw_basic=2*pi*f_basic;f_H=500;%截止频率500Hzf_simple=20000;%采样频率20kHzPointNumber = 100000;%坐标点数量x=0PointNumber-1;Standard =2+sin(w_basic*x*0.0000005);%原始标准信号noise = 0+0.1*randn(1,PointNumber);AddNoise=Standard+noise;a=2*pi*f_H/f_simple;y_last=0;y_now=0;for i = 0PointNumber-1x_now=AddNoise(i+1);y_now=(1-a)*y_last+a*x_now;output(i+1)=y_now;y_last=y_now;endfigure(4);X=0PointNumber-1;plot(X,AddNoise,'-.g');hold on;plot(X,Standard,'-..b');hold on;plot(X,output,'-..r');hold on;legend('With noise','Standard','Output')xlabel('time');ylabel('value');title('一阶低通滤波器（fH=500Hz）');
直流信号部分：
f_basic=1;%原信号频率为200Hzw_basic=2*pi*f_basic;f_H=500;%截止频率500Hzf_simple=20000;%采样频率20kHzPointNumber = 100000;%坐标点数量x=0PointNumber-1;Standard =2+0.05*sin(w_basic*x*0.00005);%原始标准信号noise = 0+0.05*randn(1,PointNumber);AddNoise=Standard+noise;a=2*pi*f_H/f_simple;y_last=0;y_now=0;for i = 0PointNumber-1x_now=AddNoise(i+1);y_now=(1-a)*y_last+a*x_now;output(i+1)=y_now;y_last=y_now;endfigure(1);X=0PointNumber-1;plot(X,AddNoise,'-.g');hold on;plot(X,output,'-..r');hold on;xlabel('time');ylabel('value');title('一阶低通滤波器（直流信号测试）');f_H=1;%截止频率500Hza=2*pi*f_H/f_simple;y_last=0;y_now=0;for i = 0PointNumber-1x_now=AddNoise(i+1);y_now=(1-a)*y_last+a*x_now;output(i+1)=y_now;y_last=y_now;endplot(X,output,'-..c');hold on;f_H=0.5;%截止频率500Hza=2*pi*f_H/f_simple;y_last=0;y_now=0;for i = 0PointNumber-1x_now=AddNoise(i+1);y_now=(1-a)*y_last+a*x_now;output(i+1)=y_now;y_last=y_now;endplot(X,output,'-..m');hold on;f_H=0.2;%截止频率500Hza=2*pi*f_H/f_simple;y_last=0;y_now=0;for i = 0PointNumber-1x_now=AddNoise(i+1);y_now=(1-a)*y_last+a*x_now;output(i+1)=y_now;y_last=y_now;endplot(X,output,'-..k');hold on;f_H=0.1;%截止频率500Hza=2*pi*f_H/f_simple;y_last=0;y_now=0;for i = 0PointNumber-1x_now=AddNoise(i+1);y_now=(1-a)*y_last+a*x_now;output(i+1)=y_now;y_last=y_now;endplot(X,output,'-..r');hold on;plot(X,Standard,'-..b');hold on;legend('With noise','Output-500Hz','Output-1Hz','Output-0.5Hz','Output-0.2Hz','Output-0.1Hz','Standard')
-
滤波器
+关注
关注
161文章
7795浏览量
177985 -
数字滤波器
+关注
关注
4文章
270浏览量
47016 -
FOC
+关注
关注
20文章
322浏览量
42796
原文标题：“一阶数字低通滤波器”原理推导（含仿真和代码实现）
文章出处：【微信号：mcu168，微信公众号：硬件攻城狮】欢迎添加关注！文章转载请注明出处。
发布评论请先 登录
相关推荐
一阶低通滤波器的工作原理、电路结构、设计方法以及应用领域
请问SIGMASTUDIO一阶滤波器系数如何计算
关于一阶RC低通滤波器的基础知识
一阶有源低通滤波电路与最经典一阶低通滤波器电路图
一阶低通滤波器_一阶低通滤波器公式_一阶低通滤波器原理
不同低通滤波器的增益大小案例公式和电路曲线
一阶电路误差分析_RC有源低通滤波器的一阶二阶原理分析及其推导！
工商网监
评论