巴特沃斯滤波器是一种有源滤波器,其通带的频率响应相对平坦。由于这种频率响应,巴特沃斯滤波器也被称为平坦滤波器。
使用巴特沃斯滤波器技术,可以设计所有类型的滤波器,包括高通、低通、带通等。在本文当中,小编将重点介绍下使用巴特沃斯滤波器技术进行低通滤波器设计。
众所周知,在设计滤波器电路时主要有三个考虑因素,它们是:
通带的响应必须是最大平坦度
从通带到阻带必须有一个缓慢的过渡
滤波器在通带内无任何失真地通过信号的能力。
通常情况下,这些失真通常是由波形的相移引起的。除了这三个,上升和下降时间参数也起着重要作用。所以,为了获得最大的平坦响应,设计了巴特沃斯滤波器。而为了从通带到阻带的缓慢过渡,设计了切比雪夫滤波器,并设计了最大平坦时间延迟贝塞尔滤波器。
巴特沃斯滤波器
以从通带到阻带的过渡介质的陡度为代价,巴特沃斯滤波器将在输出信号中提供平坦的响应。因此,它也被称为最大平坦幅度滤波器。
滤波器的衰减响应速率由电路中的极数决定,极数将取决于电路中电抗元件的数量,即电路中使用的电感器或电容器的数量。
n阶巴特沃斯滤波器的幅度响应如下:
V out / V in = 1 / √{1 + (f / f c ) 2n }
其中“n”是电路中的极数。随着“n”值的增加,滤波器响应的平坦度也会增加。'f' = 电路的工作频率,'f c ' = 电路的中心频率或截止频率。
这些滤波器具有预先确定的考虑,其应用主要用于较高频率的有源RC电路。尽管它不提供尖锐的截止响应,但它通常被认为是在许多应用中使用的全能滤波器。
巴特沃斯滤波器近似值
为了满足滤波器响应的考虑并获得接近理想滤波器的近似值,需要具有更高阶的滤波器,这将增加器复杂性。 此外,低通和高通电路具有输出频率响应和相位响应,所以理想的滤波器特性是最大平坦度、最大通带增益和最大阻带衰减。
要设计滤波器,需要适当的传递函数。为了满足这些传递函数,在具有许多近似函数的vwin 滤波器设计中进行了数学推导。
在此类设计中,巴特沃斯滤波器是其中一种滤波器类型,而低通巴特沃斯设计考虑主要用于许多功能。
一阶低通巴特沃斯滤波器
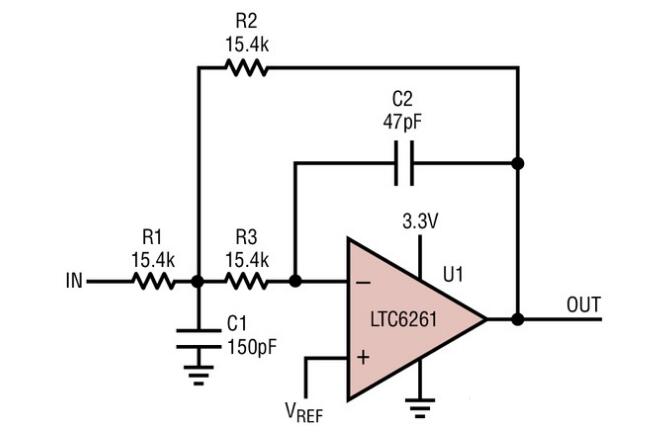
下面的电路显示了低通巴特沃斯滤波器。
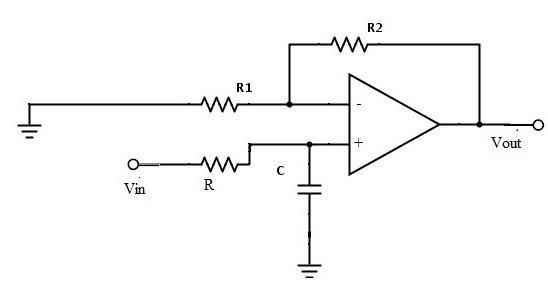
巴特沃斯滤波器所需的通带增益主要取决于“R1”和“Rf”的电阻值,滤波器的截止频率将取决于上述电路中的R和C元件。
滤波器的增益为:A_max=1+R1/Rf
电容器“C”的阻抗由-jX C 给出,电容器两端的电压为:
V c = – jX C / (R – jX C ) * Vin
其中XC = 1 / (2πfc)
极性形式的滤波器的传递函数为:
H(jω) = |Vout/Vin| ∟ø
其中滤波器增益:V out / V in = A max / √{1 + (f/f H )²},而相位角Ø= – tan -1 ( f/f H )
在较低频率下意味着当工作频率低于截止频率时,通带增益等于最大增益。
V out / V in = A max,即平衡常数。
在较高频率下意味着当工作频率高于截止频率时,则增益小于最大增益。
Vout / Vin < Amax
当工作频率等于截止频率时,传递函数等于Amax /√2。增益的下降率为20dB/decade或者6dB/octave,可以在响应斜率中表示为-20dB/decade。
二阶低通巴特沃斯滤波器
连接到一阶巴特沃斯滤波器的附加RC网络为我们提供了二阶低通滤波器。这种二阶低通滤波器的优点是增益在截止频率之后在阻带中滚降得非常快。
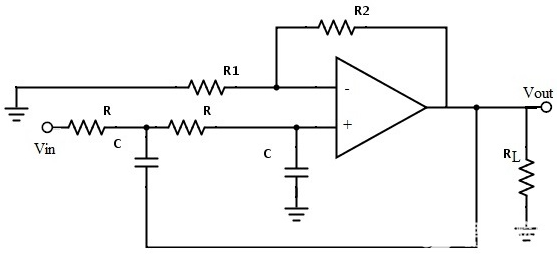
在这个二阶滤波器中,截止频率值取决于两个RC部分的电阻和电容值。截止频率使用以下公式计算:
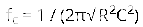
增益以40dB/decade的速率下降,该响应以斜率-40dB/decade显示。滤波器的传递函数可以表示为:
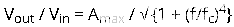
二阶滤波器传递函数的标准形式为:
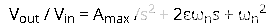
其中 ω n = 振荡的固有频率 =
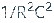
,ε = 阻尼系数 = (3 – A max ) / 2
对于二阶巴特沃斯滤波器,所需的中间项是sqrt(2) = 1.414,从归一化巴特沃斯多项式是:
3 – Amax = √2 = 1.414
为了确保输出滤波器响应,增益Amax必须为 1.586。
通过级联一阶和二阶巴特沃斯滤波器获得高阶巴特沃斯滤波器。这可以显示如下:
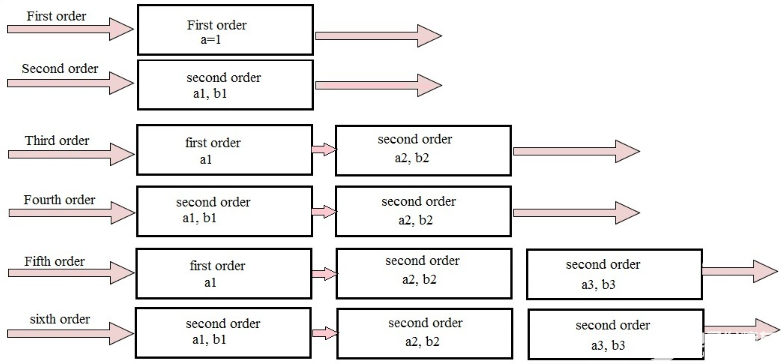
其中a n和b n 是预先确定的滤波器系数,它们用于生成所需的传递函数。
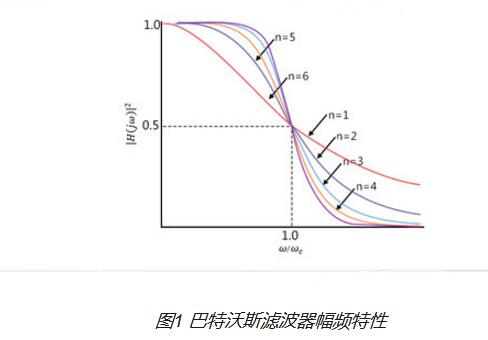
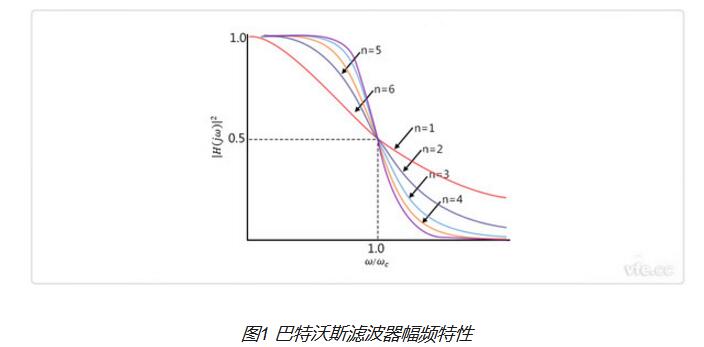
巴特沃斯滤波器的理想频率响应
输出响应的平坦度随着滤波器阶数的增加而增加,不同阶数的巴特沃斯滤波器的增益和归一化响应如下所示。
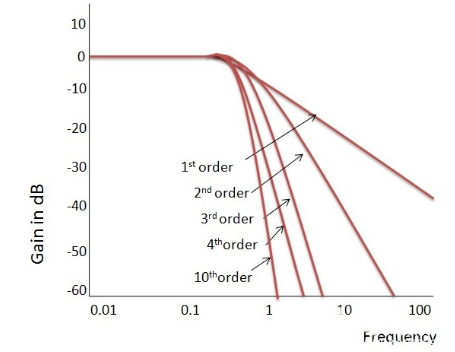
归一化低通巴特沃斯滤波器多项式
归一化是电压、电流或阻抗除以相同测量单位的数量的过程,此过程用于生成特定值的无量纲范围或水平。
滤波器传递函数的分母多项式为我们提供了巴特沃斯多项式。如果考虑一个以原点为中心的半径相等的圆上的s平面,那么巴特沃斯滤波器的所有极点都位于该s平面的左半边。
对于任何阶滤波器,“s”的最高功率的系数应始终为1,对于任何阶滤波器,常数项始终为1。对于偶数阶滤波器,所有多项式因子本质上都是二次的。对于奇数阶滤波器,除一阶外,所有多项式都是二次的,对于一阶滤波器,多项式为 1+s。
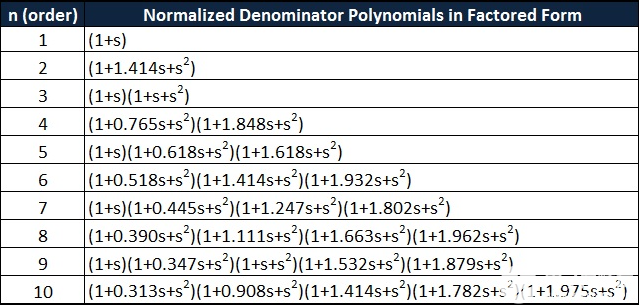
系数形式的巴特沃斯多项式如下表所示。
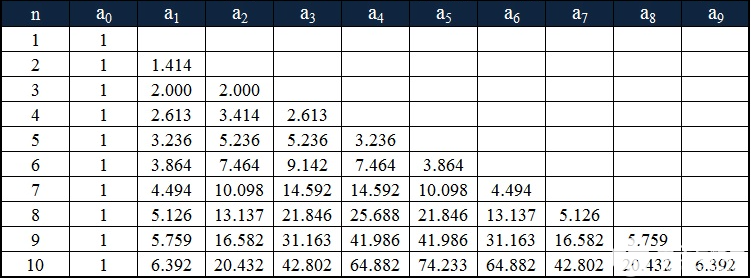
n阶巴特沃斯滤波器的传递函数如下:
H (jω) = 1 / {{1 + ε² (ω / ω c ) 2n }
其中n是滤波器的阶数,ω是弧度频率,它等于2πf,ε为最大通带增益,即Amax。
三阶巴特沃斯低通滤波器
一阶和二阶巴特沃斯滤波器的级联连接给出了三阶巴特沃斯滤波器,三阶巴特沃斯滤波器电路如下图所示。
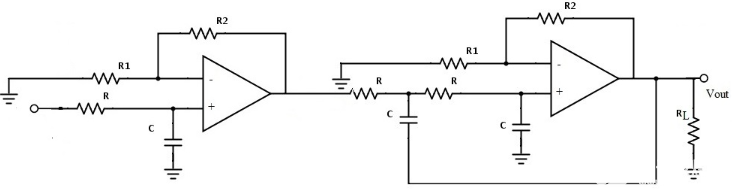
对于三阶低通滤波器,给定的归一化低通巴特沃斯多项式的多项式为 (1+s) (1+s+s²),该滤波器包含三个未知系数,它们是 a 0、a 1、a 2。
它们的系数值为a 0 = 1、a 1 = 2 和a 2 = 2。与一阶滤波器相比,该三阶巴特沃斯滤波器的曲线平坦度增加。
巴特沃斯滤波器的应用
由于其最大平坦通带特性,它在数据转换器应用中用作抗混叠滤波器。
在雷达中有应用,例如设计雷达目标轨迹的显示。
在高质量音频应用中使用巴特沃斯滤波器。
用于运动分析的数字滤波器。
巴特沃斯低通滤波器示例
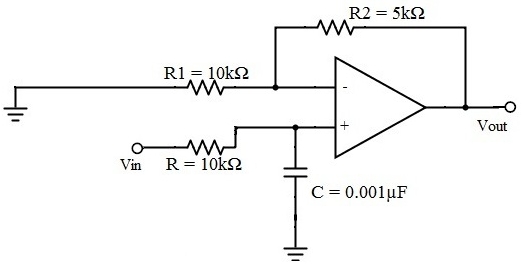
以截止频率为15.9 kHz、通带增益为1.5且电容器C=0.001µF的巴特沃斯低通滤波器为例:
fc = 1/2πRC
15.9 * 10³ = 1 / {2πR1 * 0.001 * 10-6}
R = 10kΩ
Amax = 1.5,并假设R1=10 kΩ
Amax = 1 + {Rf / R1}
Rf = 5 kΩ
总结
巴特沃斯滤波器就是电子滤波器的一种,也被称作最大平坦滤波器,其主要特点是通频带内的频率响应曲线最大限度平坦,没有纹波,而在阻频带则逐渐下降为零。
简单来说,巴特沃斯滤波器是滤波器的一种设计分类,类同于切比雪夫滤波器,可以设计成高通,低通,带通等多种滤波器。
-
滤波器
+关注
关注
161文章
7795浏览量
177989 -
巴特沃斯滤波器
+关注
关注
0文章
16浏览量
7333
发布评论请先 登录
相关推荐




 巴特沃斯滤波器的计算公式
巴特沃斯滤波器的计算公式










评论