假设您想根据内容和主题对数百(或数千)个文档进行分类,或者您希望出于某种原因将不同的图像组合在一起。或者更重要的是,假设你有相同的数据已经被分类但是你想要挑战这个标签,您想知道数据分类是否有意义,或者是否可以改进。
好吧,我的建议是你对数据进行聚类。信息经常会因为冗余等各种原因变得模糊不清,而将数据分组到具有相似特征的群集(群集)中是一种有效的方式。
聚类是一种广泛用于查找具有相似特征的观察组(称为聚类)的技术。此过程不是由特定目的驱动的,这意味着您不必专门告诉您的算法如何对这些观察进行分组,因为它是独立进行(组有机地形成)分组的。结果是,同一组中的观察(或数据点)在它们之间比另一组中的其他观察更相似。目标是获得尽可能相似的同一组中的数据点,并使不同组中的数据点尽可能不相似。
K-means非常适合探索性分析,非常适合了解您的数据并提供几乎所有数据类型的见解。无论是图像、图形还是文本,K-means都非常灵活,几乎可以满足所有需求。
无监督学习中的摇滚明星之一
聚类(包括K均值聚类)是一种用于数据分类的无监督学习技术。
无监督学习意味着没有输出变量来指导学习过程(没有这个或那个,没有对错),数据由算法来探索以发现模式。我们只观察这些特征,但没有对结果进行确定的测量值,因为我们想要找出它们。
与监督学习不同的是,非监督学习技术不使用带标签的数据,算法需要自己去发现数据中的结构。
在聚类技术领域中,K-means可能是最常见和经常使用的技术之一。K-means使用迭代细化方法,基于用户定义的集群数量(由变量K表示)和数据集来产生其最终聚类。例如,如果将K设置为3,则数据集将分组为3个群集,如果将K设置为4,则将数据分组为4个群集,依此类推。
K-means从任意选择的数据点开始,作为数据组的提议方法,并迭代地重新计算新的均值,以便收敛到数据点的最终聚类。
但是,如果您只提供一个值(K),算法如何决定如何对数据进行分组?当您定义K的值时,您实际上是在告诉算法您需要多少均值或质心(如果设置K = 3,则创建了3个均值或质心,其中包含3个聚类)。质心是表示聚类中心的数据点(均值),它可能不一定是数据集的成员。
这就是算法的工作原理:
K个质心是随机创建的(基于预定义的K值)
K-means将数据集中的每个数据点分配到最近的质心(最小化它们之间的欧几里德距离),这意味着如果数据点比任何其他质心更接近该群集的质心,则认为该数据点位于特定集群中。
然后K-means通过获取分配给该质心集群的所有数据点的平均值来重新计算质心,从而减少与前一步骤相关的集群内总方差。K均值中的“均值”是指对数据求均值并找到新的质心。
该算法在步骤2和3之间迭代,直到满足一些标准(例如最小化数据点与其对应质心的距离之和,达到最大迭代次数,质心值不变或数据点没有变化集群)
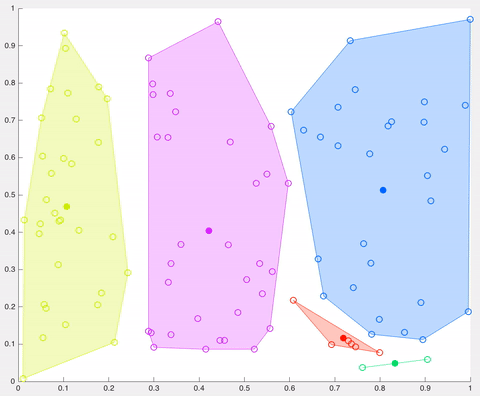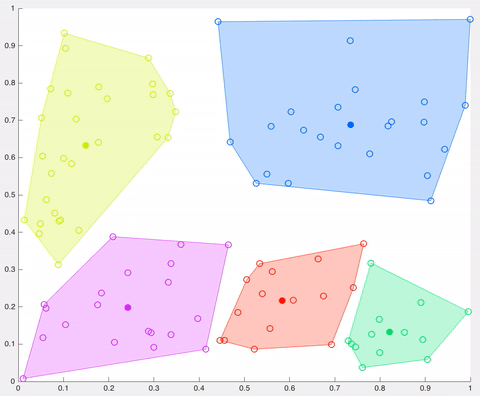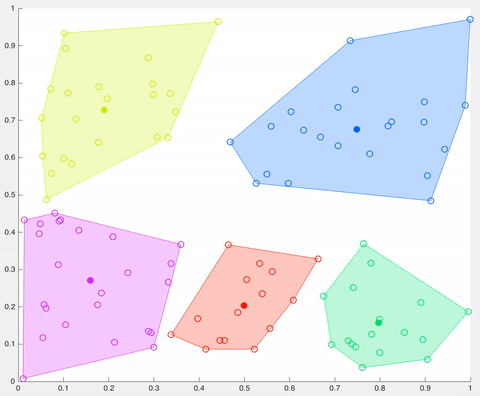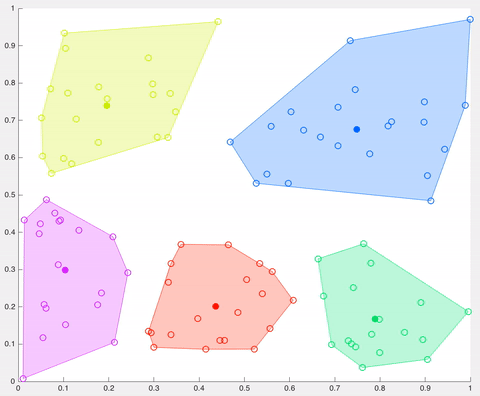
在该示例中,经过5次迭代之后,计算的质心保持相同,并且数据点不再交换集群(算法收敛)。这里,每个质心都显示为一个深色的数据点。
运行此算法的初始结果可能不是最佳结果,并且使用不同的随机起始质心重新运行它可能提供更好的性能(不同的初始对象可能产生不同的聚类结果)。出于这个原因,通常的做法是使用不同的起点多次运行算法,并评估不同的初始化方法(例如Forgy或Kaufman方法)。
但另一个问题出现了:你如何知道K的正确值,或者要创建多少个质心?对此这个问题没有普遍的答案,虽然质心或集群的最佳数量还不是先验的,但是存在不同的方法来估计它。一种常用的方法是测试不同数量的集群并测量得到的误差平方之和,选择K值,在该值处增加将导致误差和减小的非常小,而减小时将急剧增加误差和。定义最佳集群数的这一点被称为“肘点”,可以用作一个视觉度量来找到K值的最佳选择。
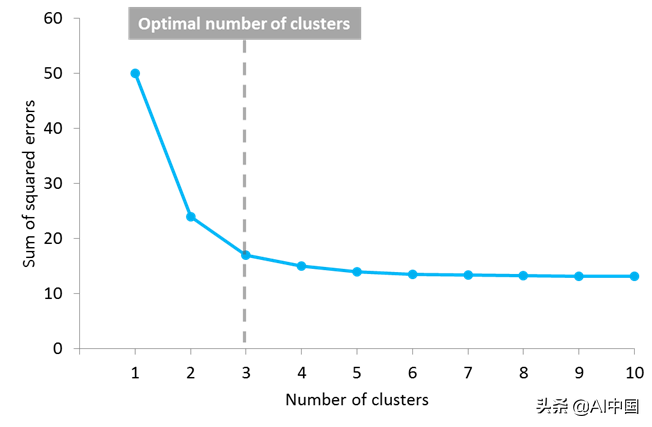
在此示例中,肘点位于3个集群中
K-means是您的数据科学工具包中必不可少的,有几个原因。首先,它易于实现并带来高效的性能。毕竟,您只需要定义一个参数(K的值)来查看结果。它的速度很快并且可以很好地处理大型数据集,使其能够处理当前的海量数据。它非常灵活,可以与几乎任何数据类型一起使用,其结果易于解释,并且比其他算法更易于解释。此外,该算法非常受欢迎,您几乎可以在任何学科中找到用例和实现。
但凡事都有不利的一面
K-means也存在一些缺点。第一个是你需要定义集群的数量,这个决定会严重影响结果。此外,由于初始质心的位置是随机的,因此结果可能不具有可比性并且显示缺乏一致性。K-means生成具有统一大小的聚类(每个聚类具有大致相同的观察量),即使数据可能以不同的方式运行,并且它对异常值和噪声数据非常敏感。此外,它假设每个聚类中的数据点被建模为位于该聚类质心周围的球体内(球形限制),但是当违反此条件(或任何先前的条件)时,算法可以以非直观的方式运行。
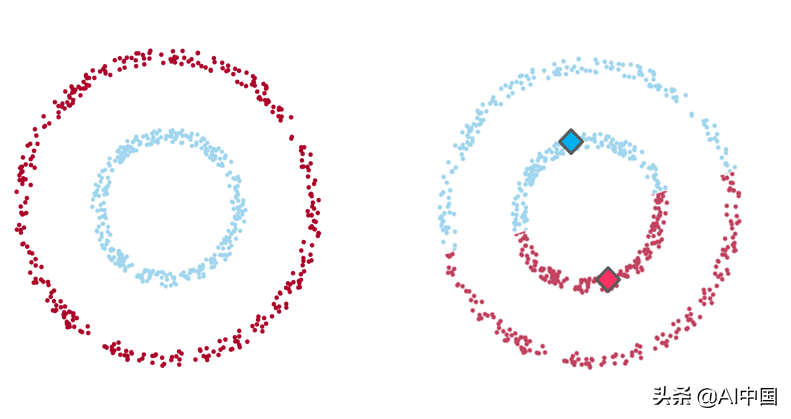
例1
示例1:在左侧,数据的直观聚类,两组数据点之间有明显分离(由一个较大的数据点包围的一个小环的形状)。在右侧,通过K均值算法(K值为2)聚类的相同数据点,其中每个质心用菱形表示。如您所见,该算法无法识别直观的聚类。
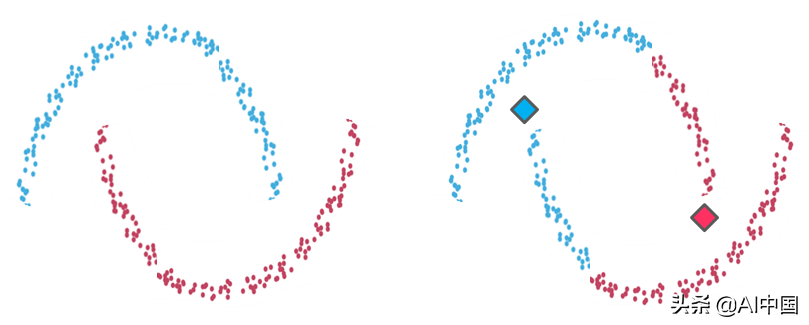
例2
示例2:左侧是两个可识别数据组的聚类。在右侧,K-means聚类在相同数据点上的结果不适合直观的聚类。与示例1的情况一样,由于算法的球形限制,K-means创建的分区不能反映我们在视觉上识别的内容。它试图找到围绕它们的整个数据球体的质心,并且当聚类的几何形状偏离球体时表现很差。

例3
示例3:再次,在左侧有两个清晰的集群(一个小而紧密的数据组和另一个较大且分散的集群),K-means无法识别(右侧)。这里,为了平衡两个数据组之间的集群内距离并生成具有统一大小的集群,该算法混合两个数据组并创建2个不代表数据集的人工集群。
有趣的是,无论这些数据点之间的关系多么明显,K-means都不允许彼此远离的数据点共享同一个集群。
现在做什么?
事情是现实生活中的数据几乎总是复杂、杂乱无章和嘈杂的。现实世界中的情况很少能反映出明确的条件,即可立即应用这些类型的算法。在K-means算法的情况下,预计至少有一个假设会被违反,因此我们不仅要识别它,还需要知道在这种情况下该做什么。
好消息是还有其他选择,可以纠正缺陷。例如,将数据转换为极坐标可以解决我们在示例1中描述的球形限制。如果发现严重的限制,还可以考虑使用其他类型的聚类算法。可能的方法是使用基于密度或基于层次的算法,这些算法修复了一些K均值限制(但也有其自身的局限性)。
总之,K-means是一种具有大量潜在用途的精彩算法,因此它具有多种功能,几乎可用于任何类型的数据分组。但是从来没有免费的午餐:如果你不想被引导到错误的结果,你需要了解它的假设和它的运作方式。
审核编辑 :李倩
-
聚类算法
+关注
关注
2文章
118浏览量
12126 -
K-means
+关注
关注
0文章
28浏览量
11292
原文标题:一个完整的K-means聚类算法指南!
文章出处:【微信号:vision263com,微信公众号:新机器视觉】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐




 K-means聚类算法指南
K-means聚类算法指南











评论