史密斯圆图的一种球面表示法
在哥伦比亚（Christopher Columbus）航行前，所有人都认为地球是平的… 。在过去的许多年中，我将传统的史密斯圆图进行扩展来帮助我理解射频领域中像振荡器设计以及放大器的稳定性这类涉及到负阻抗器件的问题。其概念使得我对于与阻抗有关问题的本质有了更深的理解，并且也证明了这是一个很有用的附加的设计辅助工具。最近，在餐桌上与其他工程师讨论时，我提到了自己的一些想法。这些想法得到了大家的认可，从那时起，他们多次说服我将自己对史密斯圆图的扩展发表出来。为此，在这篇文章中，我试图用最简单的方法来解释基于众所周知的史密斯圆图基础上的概念性辅助设计工具背后的思想。
史密斯圆图的最大优点在于它实际上是一个“图形计算器”。可以通过在史密斯图上画线来获得阻抗匹配的结果，而无需进行冗长的数学计算。所有工程师都可以使用这个工具，并且能帮助他们开发对可选择的匹配网络的 直觉认识。确实，当一个工程师对史密斯圆图开始理解，并且在他的脑海中有一个史密斯圆图时，便有可能预先将潜在的匹配方案直观化。
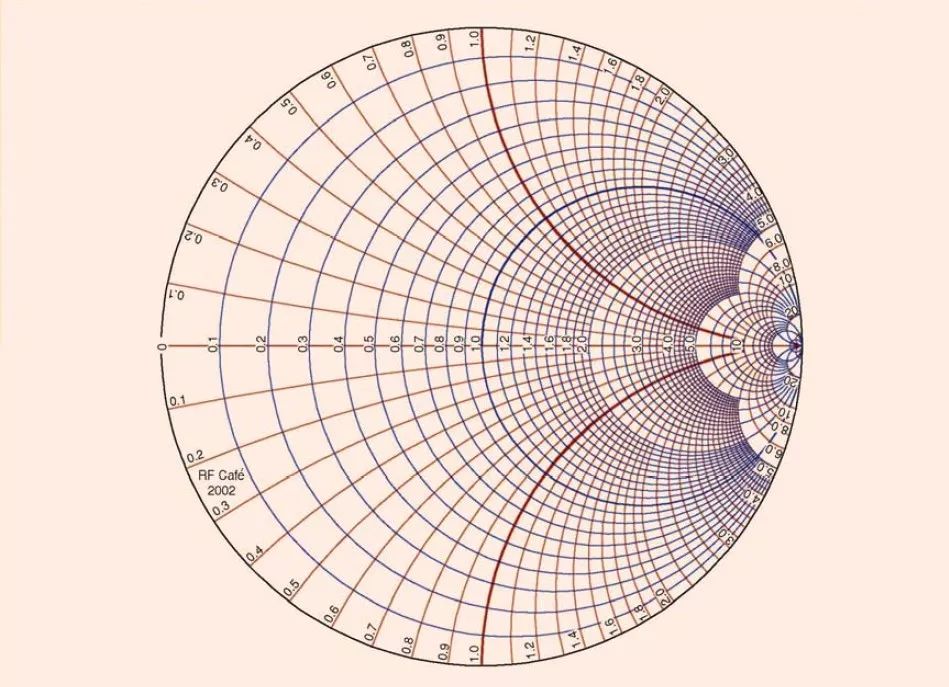
图1 传统的归一化的史密斯阻抗圆图（图形由RF Café 2002 提供）
本文所讨论的史密斯圆图的扩展是将平面二维（2-D）的圆图（例如一片纸或计算机屏幕）移到一个球面的三维圆图（ 3-D ）上。这种形式的史密斯圆图可以很方便地来处理整个阻抗区域。当然，这个新的3-D 史密斯圆图也可以通过使用合适的坐标变换和三维坐标体系而用数学式子表达出来；然而，这个工作超出了本文的范围。
已经存在一些所谓的3-D 史密斯圆图。但这些图基本上是标准的二维史密斯圆图，只是将轮廓上的数据转换到一定高度的第三维上。据作者所知，本文所做的工作才是第一个真正的三维史密斯圆图。该三维圆图的实现是在使用了一个球体和球型坐标体系的基础上完成的。
本文假设读者对史密斯圆图已经有了基本的了解。我们不打算在这里补习有关史密斯圆图的知识。有许多关于传输线理论和射频匹配的书籍可供读者参考。例如，参考文献[1]，[2]。本文刻意地保持描述的简单性，避免使用令人恐惧的数学表达式。
史密斯圆图的起源
史密斯圆图是由Philip H.Smith 提出和开发的。文献[3]介绍了Philip H.Smith 的生平。史密斯曾经在新泽西州的贝尔电话实验室工作。在他作为传输线工程师为实验室工作期间，史密斯发表了2 篇有关他所做工作的重要文章[4]，[5]。图1 便是众所周知的史密斯圆图。
最早的史密斯圆图是作为纸上计算的辅助工具的。可以购买到已经预先印刷好的圆图卡片。设计工程师们随后便可以通过使用铅笔，尺子和圆规来完成阻抗匹配的工作。近来，射频设计工作几乎完全是在使用计算机的基础上进行的。精密的计算机辅助（CAD）工具可以解决难度更大的问题并且减少了设计时间。然而，广泛使用的CAD 并没有减少史密斯圆图的使用率。设计软件可以将结果在史密斯圆图上显示出来。类似地，现代网络分析仪也可以将测量结果以图形形式显示在史密斯圆图上。
局限性
史密斯圆图的使用有许多吸引人的特点。这些特点包括简洁和易于使用，这是因为它将数字问题转化为图形问题，并且所有实部为正数的阻抗都可以在一个图上或一片纸上显示出来。但是传统的史密斯圆图有一个很大的局限。即涉及到负实部半边的阻抗域的处理。在将正的电阻域部分映射到清晰的圆周时（史密斯圆图的本质）所涉及的坐标变换过程中，负实数部分被扩展了。这便使得在画出具有负实数阻抗时就会有问题了。此外，-50Ω 点在半径为无穷大的圆周上。在史密斯圆图上表示负阻抗时会很尴尬。例如，在射频放大器设计和稳定化过程中需要观察稳定性圆周时。相对于史密斯圆图的尺寸来说，这些稳定性圆周的圆心和半径很容易使得圆周变得特别大。图2 就是这样一个例子。计算机设计软件可以自动调节圆图的坐标轴，可以将实数阻抗尺寸减到只有几个像素那么大。另一种方法是将稳定性圆周的圆心和圆周画在史密斯圆图的可视区域之外。
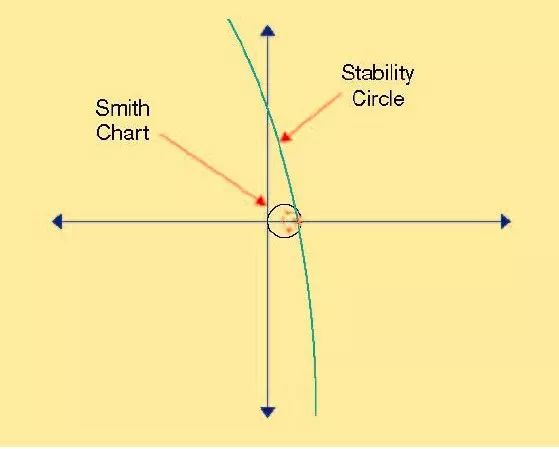
图2 一个大的稳定性圆周的例子
涉及到负电阻的另一个射频/微波设计领域是振荡器和微波有源滤波器的设计。在振荡器设计中，通过使用某种串联或并联反馈而有意识地使得有源器件处于不稳定状态。由此所产生的负电阻与谐振电路相连接。在有源滤波器的设计中，产生负电阻的目的是为了试图补偿L 和C 元件的寄生电阻的损耗。在这两种情况下，用图形法来理解阻抗变换或负载是如何影响负阻抗已被证明是很有用的。
我发现在涉及到负电阻时，用一个三维球面而不是二维圆周的方式来表示史密斯圆图时，可以更好地洞察匹配问题的实质。在下一节中，我将要讨论一种把阻抗域的负实数部半边结合进入扩展的史密斯圆图的有效方法。
需要注意的是，本文中使用的都是50Ω 史密斯阻抗圆图。虽然本文在此没有进行展示，但也可以生成球面形的史密斯导纳圆图甚至球面形的并且适合于任意阻抗的混合阻抗/导纳圆图。
史密斯圆图的扩展方法
复数形式的阻抗Z=R+jX 表示在图3 的X-Y 平面上。在这个图形中，使用字母来代表不同点的阻抗。A= -∞+0j，B= -50+0j，C=0+0j，D=50+0j 以及E=∞+0j。同样F=0-∞j，G=0-50j， H=0+50j 以及 J=0+∞j。此外，R=50Ω 是用垂直虚线画出，X=50Ω 是用水平横虚线画出的。可以看出在X-Y 平面的左半边，R 小于零（因此可以表示负电阻），X-Y 平面的右半边代表正的电阻。将
阻抗平面进行转换就生成了图4 的史密斯圆图。坐标体系转换的详细内容见[1]。从图4 可以看出，点E，F 和J现在都在圆周的右边。代表电阻和感抗为零的原点C 是在圆周的左边。而代表-50j 的电容和+50j 的电感的G 和H 则分别在圆周的底部和顶端。现在含有正实部半边的阻抗面（R>0）是在组成史密斯圆图的圆周内，而含有负实部半边的阻抗面（R<0）则在圆周之外。
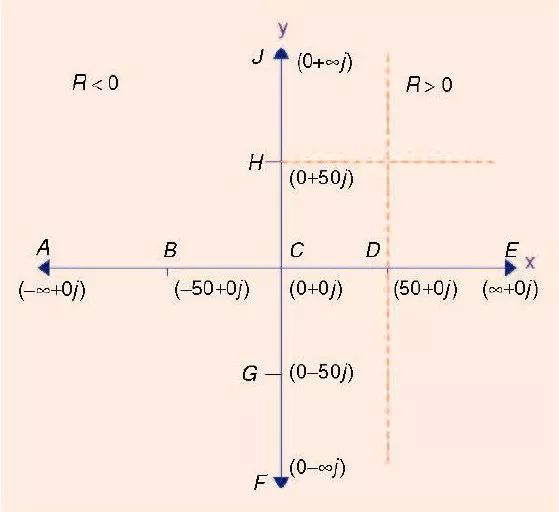
图3 阻抗平面
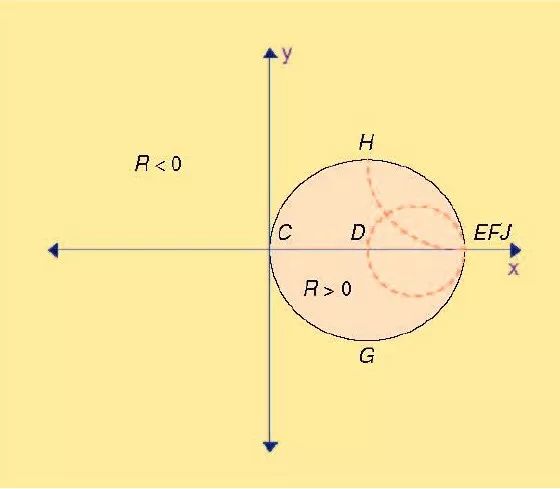
图4 按照史密斯的方法，将正实部的阻抗平面转换到圆内
图3 所示的是代表了电阻为常数和感抗为常数时的阻抗虚线，也同样显示在图4 中。遗憾的是，在系统坐标变换时，具有负实部半边的阻抗域部分被扩展了。所以，采用史密斯圆图来处理负阻抗就变得很棘手。
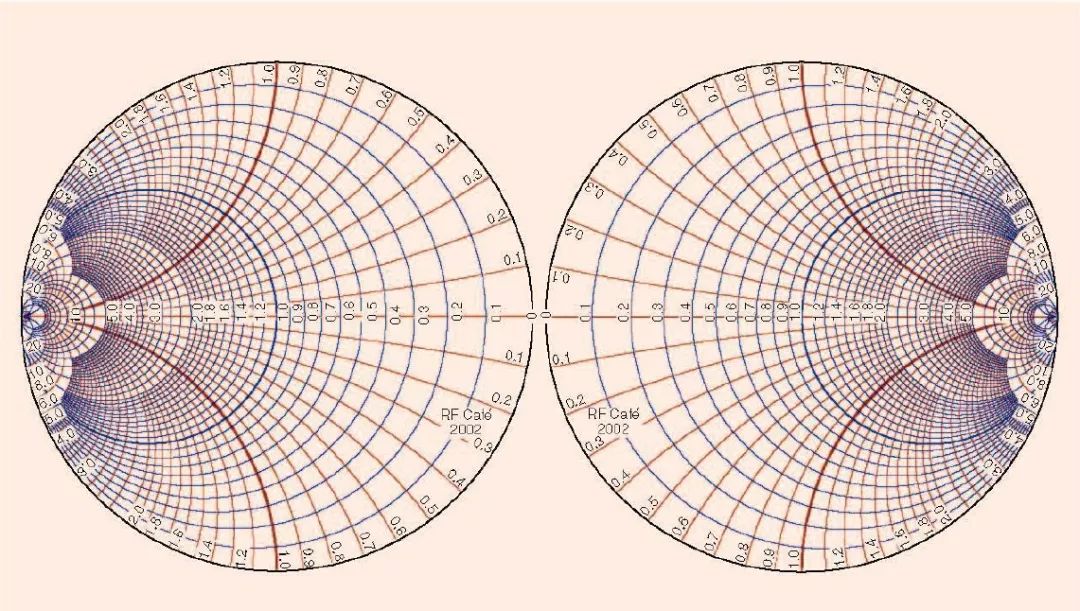
图5 一个肩并肩的可覆盖整个阻抗平面的史密斯圆图（图形由RF Café 2002 提供）
一个能将含有负实部半边的阻抗平面域压缩为易于处理的尺寸范围的可行方法是生成两个肩并肩的史密斯圆图[6]，一个圆图处理含有正实部半边的阻抗域，另一个处理含有负实部半边的阻抗域。这两个肩并肩的史密斯圆图可以帮助工程师一眼就能看到整个阻抗范围。图5 便是这样一个例子。
图6 将整个阻抗平面转换为两个肩并肩的圆
肩并肩史密斯圆图的生成是通过采用2 个坐标变换来实现的，一个变换是在阻抗平面的右边，即史密斯已经完成了的，另一个在左边，是含有负电阻半边的阻抗平面部分。
参考图3，可以看出在Y 轴上的点F，G，H 和J 在y 轴上从而组成了阻抗平面2 个半边的边界线。因此，在使用2 个坐标变换来生成2 个史密斯图时，这些点显示在对偶处。例如，对G 来说，产生图6 的对偶点G 和G´。因此这种方法的缺点是在两个图中，每个图的边界存在不连续性。例如，+50jΩ 同时出现在两个史密斯圆图中，它们之间存在一个间隔。
这个问题的解决办法之一是想像出两个背靠背的史密斯圆图，每个史密斯圆图的外边界相重叠。这样一个例子可以想像为将具有正实部的阻抗和具有负实部的史密斯圆图印刷在乒乓球拍的两面。但是从一面变换到另一面时，同样没有一个平滑的过渡。这样一来，设计工程师们就需要反复地将球拍翻来翻去。
在过去的许多年中，我将传统的史密斯圆图进行扩展来帮助自己理解射频领域中像振荡器设计以及放大器的稳定性这类涉及到负阻抗的问题。
史密斯圆图的球面扩展形式
为了生成球形的史密斯圆图，需将图 3 所示的整个阻抗域包围在球体的表面。见图7。图3 中标记的点也同样地标在了球面上。可以看出，图3 的原点（点C）现在是在球体的左边。其归一化的坐标（x，y，z）为（-1，0，0）。（注意，为了方便起见，对图3 的原点作了x=-1 的偏移。）点A，E，F 和J，即在x 和y 轴上阻抗趋于正无穷大和负无穷大的点，现在的坐标都为（1，0，0）。代表-50Ω 和+50Ω 的点B 和D，现在分别在点（0，0，-1）和（0，0，1）处。类似地，代表-50 j 和+50 j 的点G，H，现在分别在（0，-1，0）（0，1，0）处。
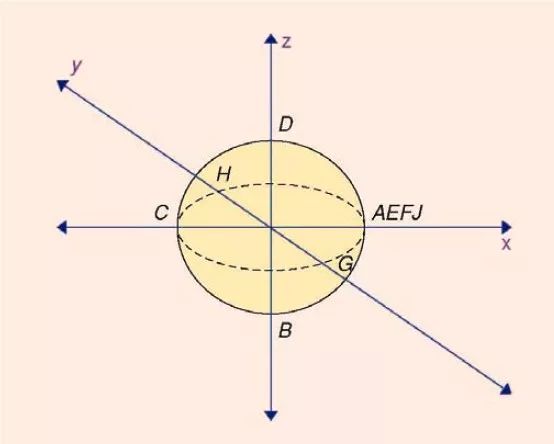
图7 转换到球体的表面后的阻抗平面
在这个新形式的史密斯圆图中，阻抗为0 和无穷时的点在x 轴上。从Z 轴的正方向去看球体，可以看到一个类似于传统的史密斯圆图。当然，由于球面的曲线特性，这个圆周的形状似乎有些变形。当把阻抗平面映射到球面上时，整个平面都在一个易于处理的区域内，而且正电阻到负电阻的过渡可以平滑连续地进行。
Z>0 的半球表面含有所有具有正电阻的阻抗，Z<0含有所有具有负电阻的阻抗。类似地，y>0 的半球含有感抗阻抗，y<0 的半球含有容抗阻抗。只有在球面上的点才有意义；在球体内的点则无关紧要。
现在球形的史密斯圆图已经建成了，正如2-D 史密斯圆图一样，我们可以考虑不同阻抗的表示方式。
首先，电阻为常数和感抗为常数的线可以先画出来。这些线形成了一系列封闭的圆周，起始和中止于点（1，0，0）。例如，+50，+50j，-50，-50j 这些常数电阻和感抗线都从点AEFJ（北极）开始，再回到起点前，跨经点D，H，B 和G（在赤道上）。画出其它值的电阻和电抗线使其类似于2-D 史密斯圆图。见图8。图8（a）是从南极（z=0）看过去的球形史密斯图，而图8（b）是从北极（z=∞）看过去的史密斯球。
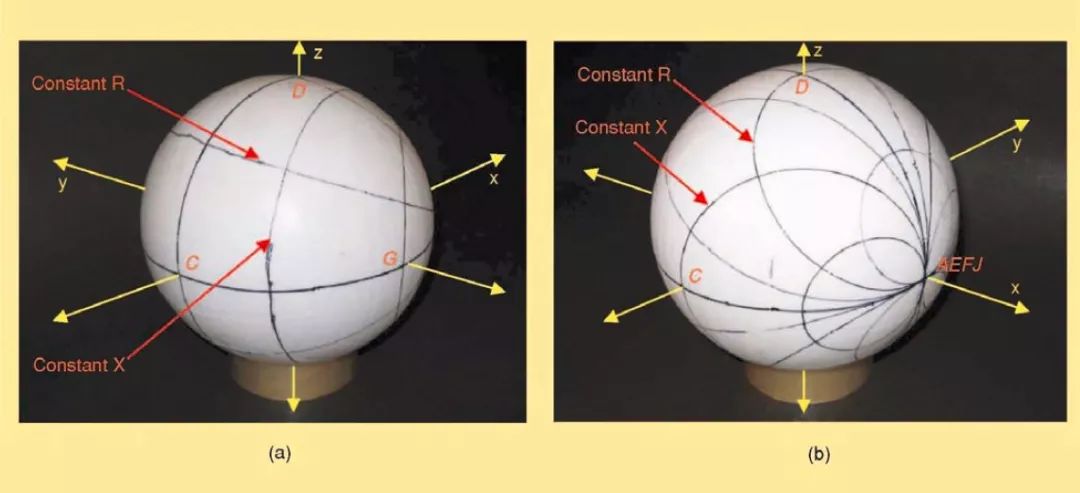
图8 画有常数电阻和感抗的球形史密斯圆图 （a）从南极看过去的球体（b）从北极看过去的球体
我们还可以考虑将常数Q（品质因数）的线画在标准史密斯圆图上。这会形成阻抗从零到无穷大的一系列弧线。当Q=0 时（理想的电阻），弧线便成为一条从零到无穷大的直线，当Q 为无穷大时（一个理想的电感或电容），弧线是沿着史密斯图的圆周线的。在球形的史密斯圆图上，Q 为常数的线便形成了从北极Z=无穷大到南极Z=0 的弧线。见图9。在x-y 平面上的Q 等值的圆周上具有一个零值，同时在x-y 平面上的具有一个Q 为无穷大的Q 等值圆周。使用球形史密斯圆图，当电阻为负的时候，也可以很容易地使用Q 线。图9 中增加了纬线。这些纬线是由|Z|为常数时所形成的。赤道线代表的是|Z|=50Ω。
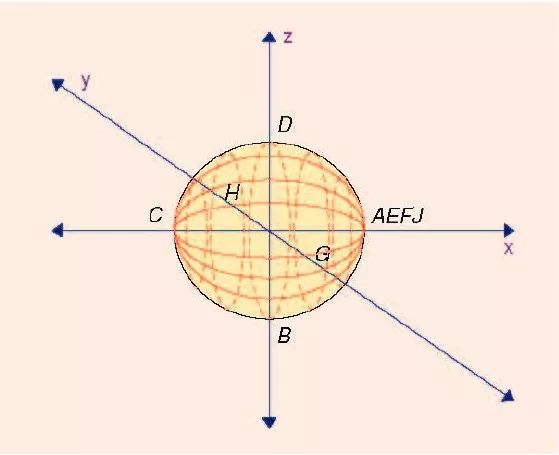
图9 绘有常数Q（实线）和常数|Z|（虚线）的球形史密斯圆图
史密斯圆图的扩展涉及到将平面 2-D的圆图转移到球面的3-D 圆图上，使用史密斯圆图有许多吸引人的特性。
在球体中将Q 看作经线，而将|Z|看作纬线相当于用极坐标而不是用迪卡尔坐标来表示史密斯圆图，其中mag(Z) （ 幅值） = Sqrt(R2+X2) ， phase(Z) （ 相位） =
arctan(X/R) = arctan(Q)。
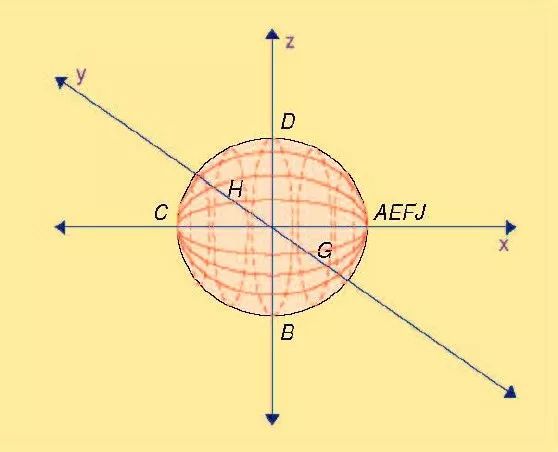
图10 绘有常数|ρ|（|虚线）和常数反射相位（实线）的球形史密斯圆图
当用到反射系数时，史密斯圆图也同样很有用。反射系数ρ 在史密斯圆图上的表示通常是针不同常数的|ρ|的值来绘出对应的曲线。这便会形成一系列的同心圆，圆心在传输线的特性阻抗点处（ 我们这里用的是50Ω）。这些同心圆在史密斯圆图的中心点处从半径为零开始，逐渐增加直至反射系数为1 时到达史密斯圆图的圆周为止。具有|ρ|>1 的反射系数也可以在图上表示出来。这种情况说明反射波大于入射波。这便为反射增益，当存在负电阻时会出现这种情况。在球形史密斯图上可以很灵巧地处理这种情况。图10 显示出了球形史密斯图上|ρ|为常数时的曲线和ρ 的相位为常数时的曲线。纬线代表的是|ρ|为常数时的曲线，经线代表的是当ρ 的相位为常数时的曲线。北极点处于50Ω，反射系数为0（匹配完美的传输线），南极是-50Ω，反射系数为无穷大。赤道对应的反射系数|ρ|=1。当考虑反射系数时，北极和南极点对应的阻抗有900的相位差。
图形方式和计算机辅助设计
史密斯圆图的2-D 特征可以很容易地印在纸上或显示在屏幕上。然而，对于3-D 史密斯圆图来说，就并非如此了。要显示史密斯圆图以及在图上画出曲线和轮廓便会有些实际上的困难。一个办法是做出打印好的小球。这会类似于一个塑料的足球，只不过代替六角形图案的是电阻和感抗曲线。图8 便是这样一个例子。在过去的许多年里，我将其放在书桌上作为设计或直观化的工具
（我以前的一个同事为小球起名为Zelley 球，每次到我办公室时都会向我仍这个球，并以此为乐）。也许，在每个本科微波授课的教室前的讲台上应当放一个这样的球，类似于地理课上的地球仪。很明显，在球上画出仿真结果和轮廓会很费事。同样，手工在图上划线无法与常规计算机自动设计流程一体化。
另一种方法是使用3-D 计算机软件。这样可以使得设计者能够通过使用计算机鼠标或键盘来旋转和转动球形史密斯圆图。有可能让设计者选择显示阻抗，导纳（或混合形式）的史密斯圆图，将Q 或反射系数叠加在球的表面。球体是不透明的或半透明的。或许可以做多个球表面的2-D 投影，这可以成为计算机辅助设计的一个值得一试的折衷方案。
结论
本文重点讨论了传统2-D 史密斯圆图的局限性。提出了一种克服这些局限的扩展史密斯圆图的想法。这种扩展包括从2-D 阻抗平面转换到三维，并将其映射到球体的表面。相信这是首次提出的史密斯圆图的转换方法。然后考虑了球形史密斯圆图的多种表示方法。包括使用常量电阻，电感，阻抗和反射系数曲线。最后，讨论了如何用图形方法来显示3-D 史密斯圆图。需要指出的是，本文这里所讨论的许多观点还没有进行严密的数学运算，所以有可能在球形的史密斯圆图
上出现一些不连续的地方。然而，基本的概念和想法是作者经过了充分思考的，是完全能够发表出来的。
希望本文所讨论的3-D 史密斯圆图可以在射频和微波设计界或者用作设计工具，或者用于直观化的帮助。希望本文至少提出了一个有趣的可供讨论的课题。
致谢
作者Chris Zelley在此深深感谢Steve Cripps 和Gord Rabjohn 的帮助和建议，以及他们对作者构思这篇文章所做的鼓励。
原文刊登于IEEE microwave magazine 作者：Chris Zelley
审核编辑：汤梓红
-
振荡器
+关注
关注
28文章
3832浏览量
139029 -
史密斯圆图
+关注
关注
1文章
20浏览量
9643
原文标题：史密斯圆图的一种球面表示法
文章出处：【微信号：射频问问，微信公众号：射频问问】欢迎添加关注！文章转载请注明出处。
发布评论请先 登录
相关推荐
史密斯圆图的一种球面表示法
如何在Ansoft designer 利用史密斯圆图做出匹配电路
应用史密斯圆图工具进行阻抗匹配的实例[分享史密斯圆图工具]
如何更方便地使用史密斯圆图
最经典的“史密斯圆图”讲解
利用史密斯圆图进行RF阻抗匹配设计
阻抗匹配与史密斯圆图
一种克服这些局限的扩展史密斯圆图的想法
工商网监
评论