本文讨论如何使用加速度计(如组合部件)提高倾斜测量精度。电动驻车制动器(EPB)用于乘用车,使车辆在平坦的道路上保持静止。这是通过使用单轴或双轴加速度计测量倾斜度来实现的。通常,x轴、y轴或z轴低g加速度计放置在EPB控制单元的专用模块中。现在,越来越多的车辆具有电子稳定控制(ESC)功能,在单个芯片中结合了低g加速度计和陀螺仪。这样做是为了防止车辆侧滑和翻车,现在通过立法要求全球范围内使用ESC功能。如果倾斜测量由组合部件(单芯片、组合加速度计和陀螺仪)完成,则无需在车辆上安装独立的 EPB 模块,这将显着降低汽车的成本。由于组合部件通常用于ESC,因此未针对倾斜感测进行优化,有时组合部件的倾斜测量精度无法满足精度要求。由于组合是 xy 轴或 xyz 轴,因此它通常使用 x 轴进行倾斜测量,而 EPB 模块中的一些传统低 g 加速度计使用 z 轴,因为它垂直安装在发动机舱中。传感轴应垂直于重力放置,以获得更好的精度 - 这将在后面讨论。
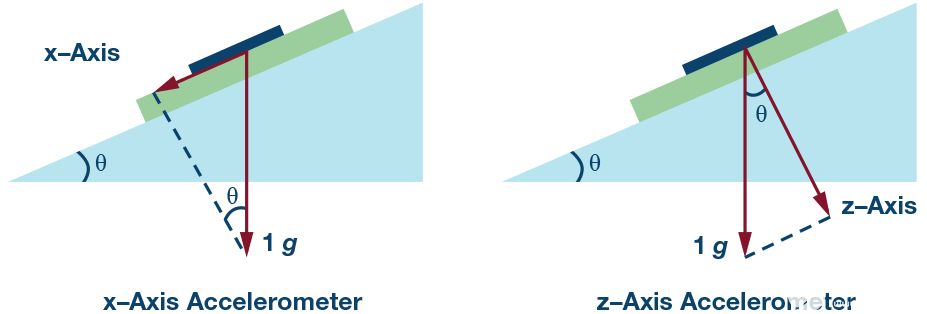
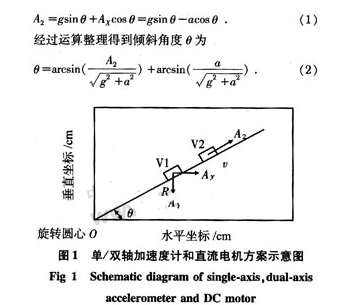
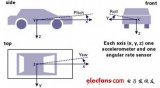
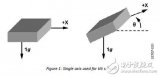
图1.x 轴和 z 轴加速度计的安装图示。
对于车辆的倾斜测量,评估精度非常重要。想象一下,您的汽车停在绝对平坦的地面上,因此加速度计计算的角度应为 0°。如果您的汽车停在坡道上,则应准确检测倾斜度,以便正确启动制动系统。
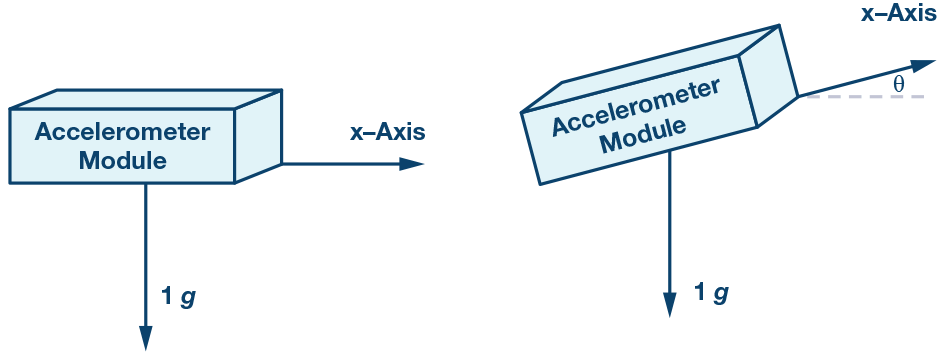
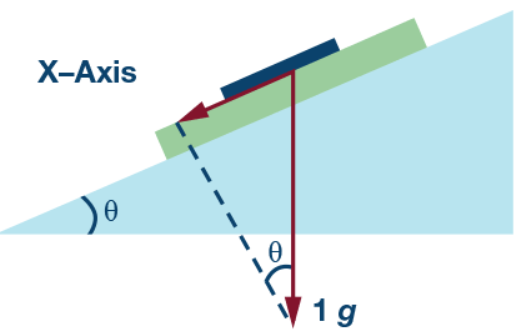
图2.X 轴感应倾斜测量图示。
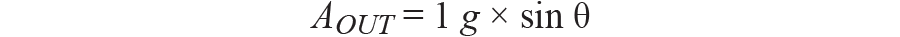
所以
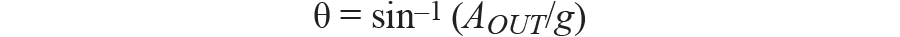
哪里:
一个外是加速度计的输出,单位为 g。
θ 是以度为单位的斜坡倾斜度。
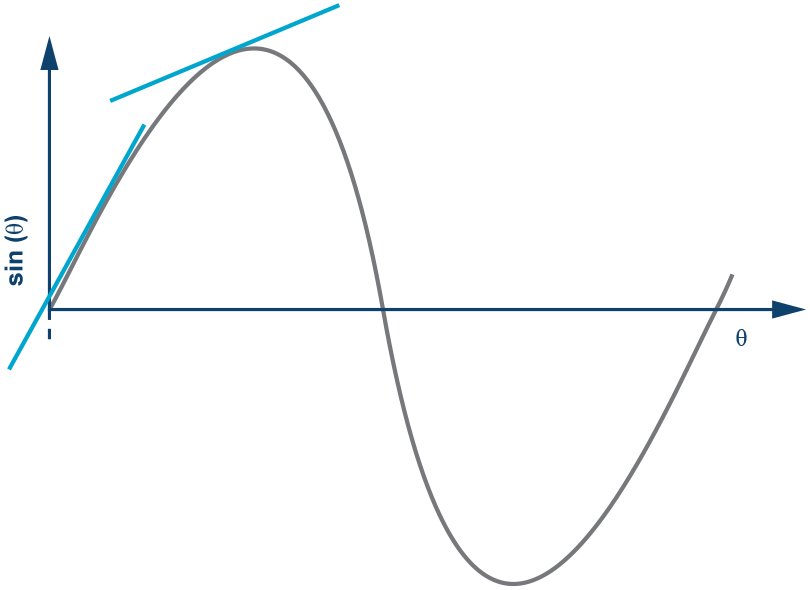
图3.罪 θ 对 θ 的敏感性随着 θ 的增加而降低
因为 sin θ 是一个非线性函数,所以一个外θ是非线性的,它在接近零时具有最佳的线性度,这意味着它具有最佳的测量精度。随着θ的增加,测量精度会降低。这就是为什么传感轴应垂直于重力放置的原因,因为道路坡度将接近于零。
对于车辆的倾斜测量,没有必要考虑具有全坡道坡度的系统。现实世界中道路上绝大多数匝道坡度不会超过30°。我们只需要分析±30°范围内的贡献精度。
有几个因素会影响系统级测量精度:
灵敏度误差和初始绝对失调
非线性
与初始绝对偏移的总偏移变化
噪声
灵敏度误差和初始绝对失调
灵敏度错误
灵敏度是测量的输入-输出传递函数的斜率,通常在 +1 g 和 –1 g 处。灵敏度误差是灵敏度的零件间偏差。例如,某些加速度计的最大灵敏度为 3%。

图4.输入输出加速度的灵敏度误差。
初始绝对偏移
该范围内的失调约为25°C;例如,25°C ± 5°C,在模块制造完成后立即测量。初始绝对偏移表示大量器件中测量的偏移值的标准偏差。
两点校准
对于倾斜测量应用,两个主要误差来自偏移误差和灵敏度误差。这两个错误会导致不可接受的传感结果,因此不应忽视它们。如果我们想消除这两部分误差,应该校准加速度的输出。通常,对倾斜测量的偏移和灵敏度进行一次性校准。如果考虑失调和灵敏度误差,加速度计的输入与输出关系为:
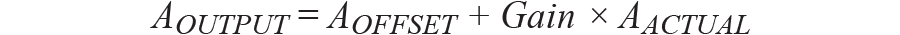
哪里:
一个输出是以 g 为单位的偏移误差。
增益是加速度计的增益,理想值为1。
一个实际是施加在加速度计上的实际加速度,单位为 g。
有两种基本的校准技术;一种是单点校准。通过在加速度计上施加0 g场,然后测量输出来完成此校准。这种校准只能用于校准失调误差,而增益误差无法校准。然后,从实际输出值中减去0 g字段中的结果输出,以消除失调误差。这是一种简单的校准方法,但不是精度方法,因为仍然存在灵敏度误差。另一种方法是 1 g 翻转校准,它将在 +1 g 和 –1 g 处使用两点校准,并在 +1 g 和 –1 g 的每个字段中测量加速度输出,如下所示:
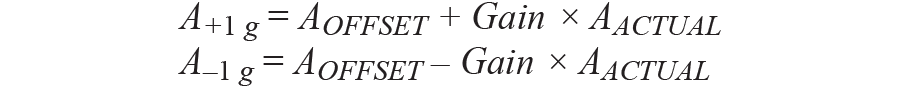
其中偏移,一个抵消,以 g 为单位。
根据这两点信息,失调和增益可以按如下方式解决:
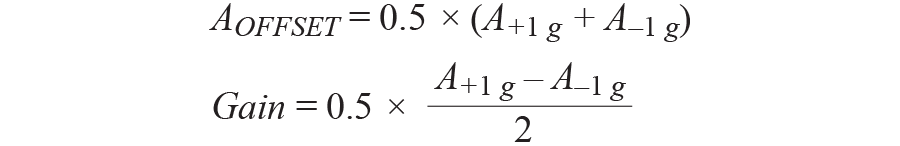
其中 +1 g 和 −1 g 测量,一个+1 克和一个–1 克,以 g 为单位。
在这种一次性校准之后,可以通过遵循此公式计算实际加速度,每次都消除偏移和灵敏度误差。
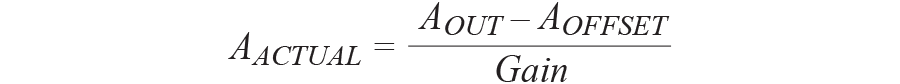
哪里一个抵消和一个外在 G 中。
非线性
器件的非线性度是测得加速度(一个多边环境协定)和理想的线性输出加速度(一个适合).加速度测量的数据集应包括加速度计的满量程范围。它以最大(|一个多边环境协定–一个适合|).
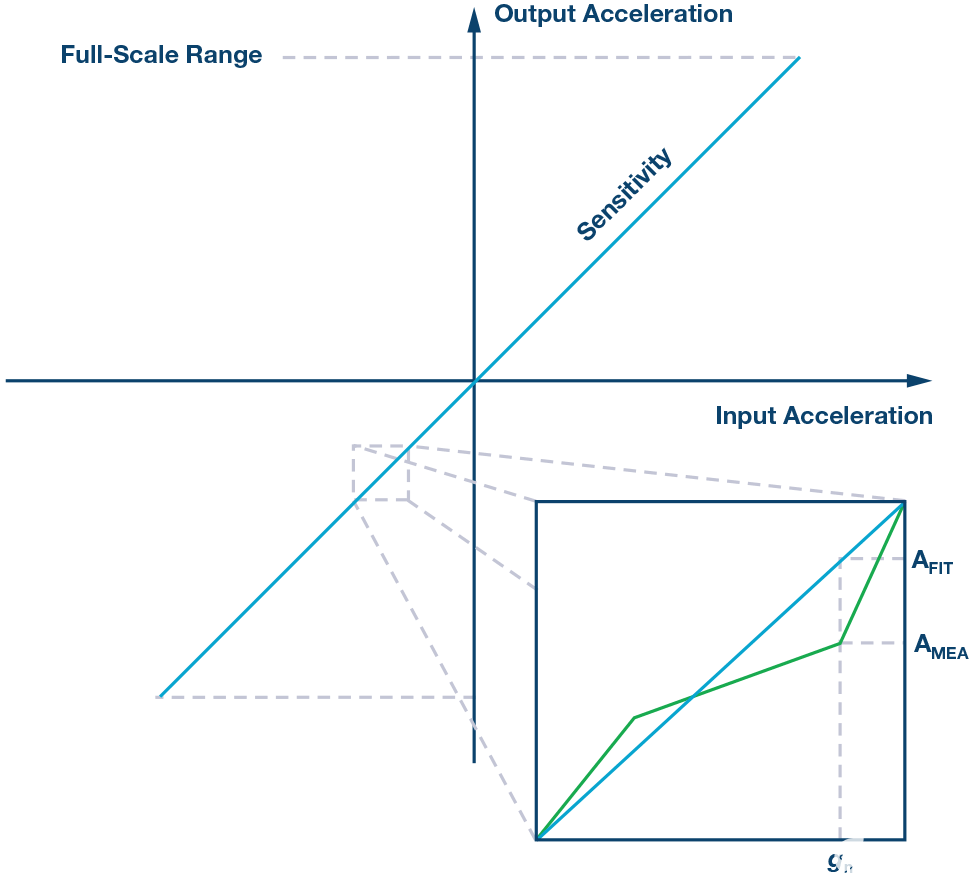
图5.器件的非线性。
哪里:
一个多边环境协定在定义的加速度下测量gn.
一个适合在定义的加速度下预测gn.
大多数加速度计或组合器件在给定的输入加速度计范围内具有非线性,例如,30 m g± 2 g的范围。对于倾斜测量应用,输入斜坡斜率在±30°以内,这意味着输出加速度范围在±500 m g(±1 g × sin 30°)以内,因此应重新评估此范围内的非线性。由于非线性在整个输入范围内不是线性的,因此很难准确和定量地评估这部分误差。但是,由于该器件的数据手册对于30 m g的非线性度和±2 g的输入范围通常非常保守,因此使用10 m g进行±500 m g以内的误差计算更为合理。
与初始绝对偏移的总偏移变化
与初始绝对失调的总失调变化是由温度、应力和老化效应引起的失调的最大偏差。该偏差是相对于给定器件的初始绝对偏移来测量的。这是对精度总误差的主要贡献。
在温度、应力、老化等所有这些因素中,变化与温度的关系占总偏移变化的主要百分比。通常,变化与温度的关系曲线是二阶曲线,通常是旋转的抛物线。为了消除这部分误差,可以在系统级别执行三点校准。对于给定器件,可以通过以下步骤校准输出变化漂移随温度的变化。
第 1 步:
器件的输出响应偏移了某个值∆N0.温度校准过程的第一步是消除环境温度下的偏移。

图6.第 1 步:在环境温度下抵消偏移。
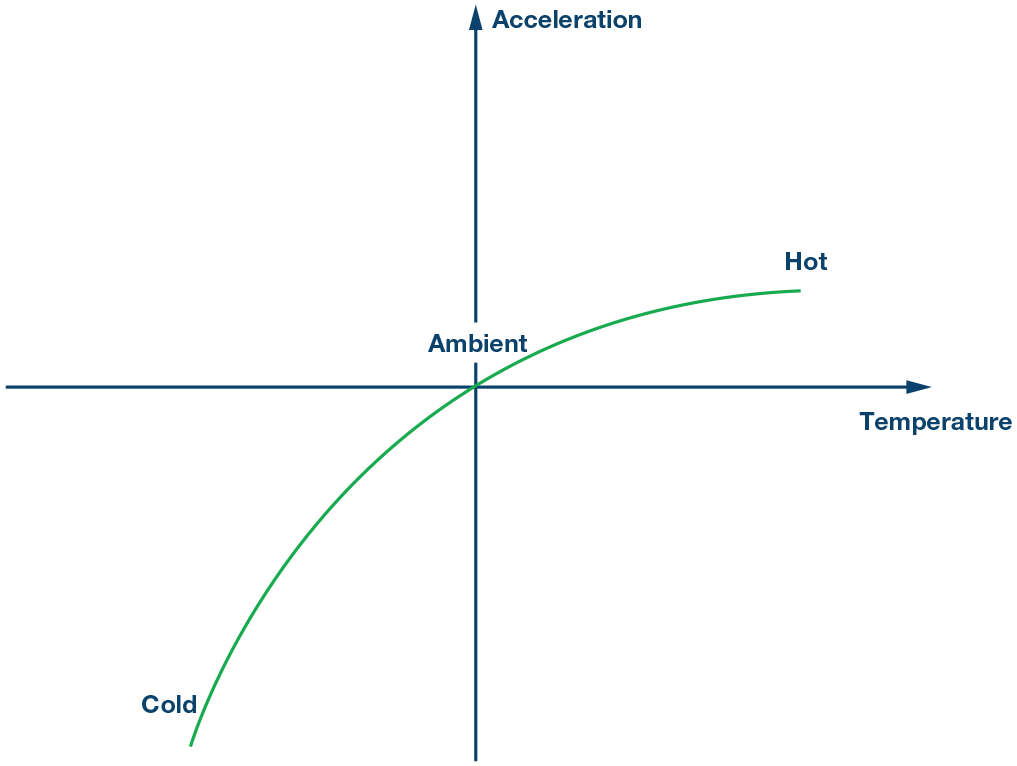
图7.第 2 步:在环境温度下取消偏移后。
第 2 步:
接下来,在高温下测试器件,并将该新信息用于生成用于失调校正的线性方程。
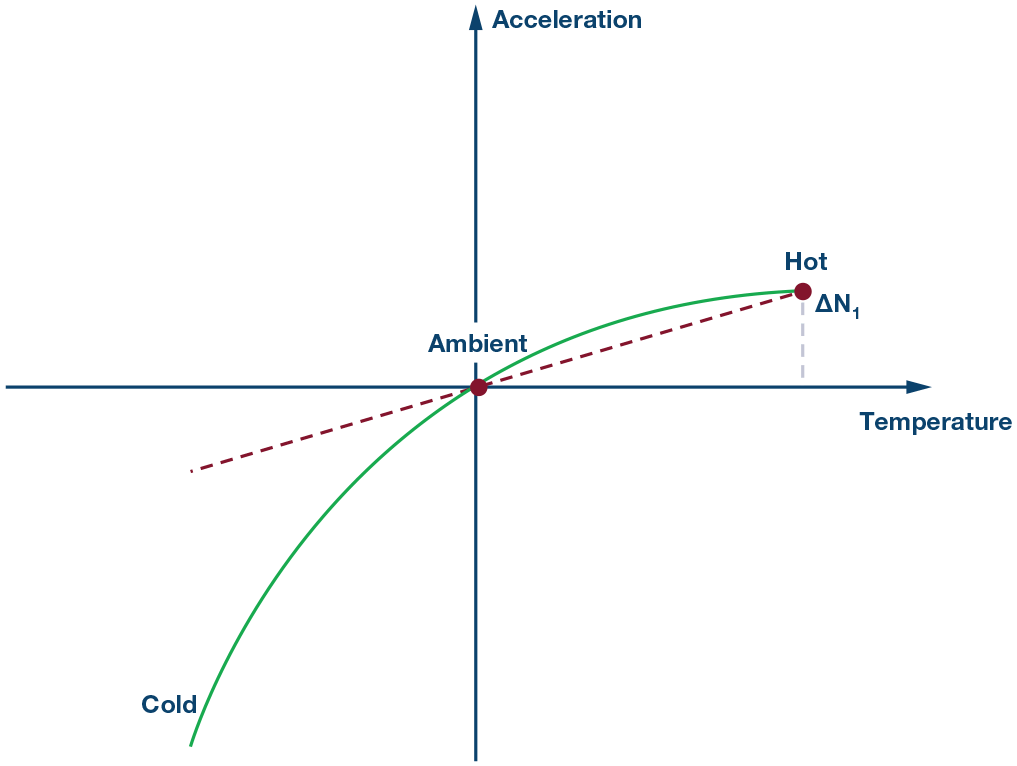
图8.步骤3:在热时抵消抛物线旋转分量。
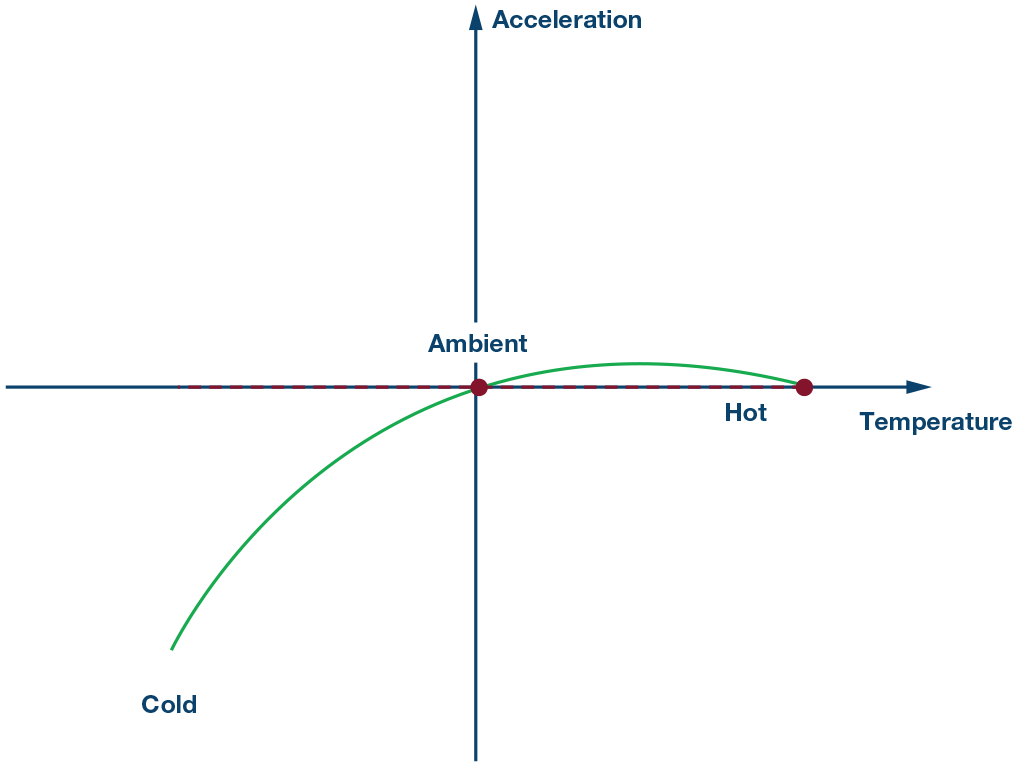
图9.步骤4:取消抛物线旋转分量后。
第 3 步:
将二阶分量添加到现有方程中,以校正偏移的其余部分。假设二阶曲线遵循以下等式:
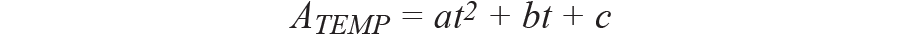
这是一个二阶抛物线公式,旋转分量已通过步骤 1 和 2 取消。
这个二阶抛物线对这个方程有三个解:
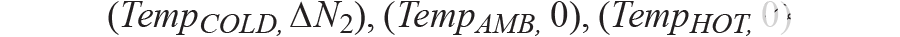
然后我们可以得到tempco a,b,c。

图 10.第 5 步:添加二阶分量以抵消残余偏移。
所有温度信息∆N0,∆N1,∆N2,a,b,c应存储在系统的非易失性存储器中,并且需要板载温度传感器。系统将在每次上电后例行校准加速度计,以确保消除变体漂移与温度的关系。
噪声
基于单个数据样本的倾斜测量可能不可靠。即使加速度计的噪音为零,倾斜测量也是在汽车开启时进行的,因此由发动机、过往车辆或乘客在车内移动引起的任何或所有振动都需要减轻。执行此操作的最佳方法是尽可能长时间地平均数据,而不会低于最低数据速率要求。这种平均将降低均方根噪声。
假设我们对噪声进行采样,我们得到的每样本方差为
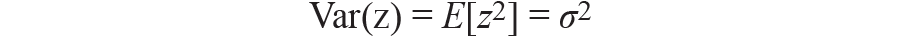
对随机变量求平均值会导致以下方差,
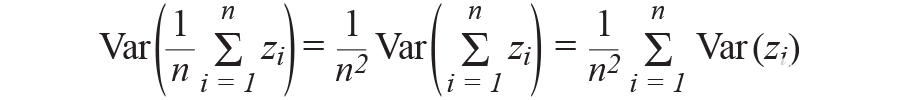
由于噪声方差在σ时是恒定的2,
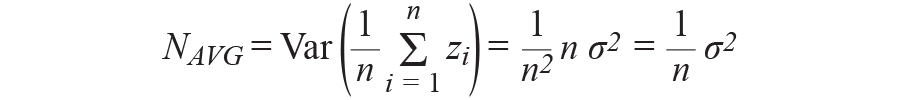
证明对相同的不相关噪声进行平均n个实现可将噪声功率降低n倍,并且均方根噪声将降低√n。
由于随机噪声受高斯分布的影响,因此均方根噪声等效于高斯分布的标准差。6σ以内的最小人口为97%。
例如,如果在1 kSPS下对每100 ms的数据求平均值,则最大均方根噪声= 0.4 m g,这意味着如果我们使用6σ作为与平均值的距离,则该点的峰值噪声计算仅为2.4 mg。
将 rms 值乘以的因素取决于部件的任务配置文件的统计需求。例如,选择6作为因子(峰峰值噪声为6 × rms噪声)将影响器件使用寿命期间发生最坏情况的概率。RMS噪声是产品数据手册中指示的固定值。它是标准差,这意味着它在 1 西格玛分布中。它不能用于计算,因为 1 西格玛分布内的遏制限值仅为 68.26%。这就是为什么我们必须选择一个更高的因子来乘以均方根噪声。更大的因素将导致更好的遏制。
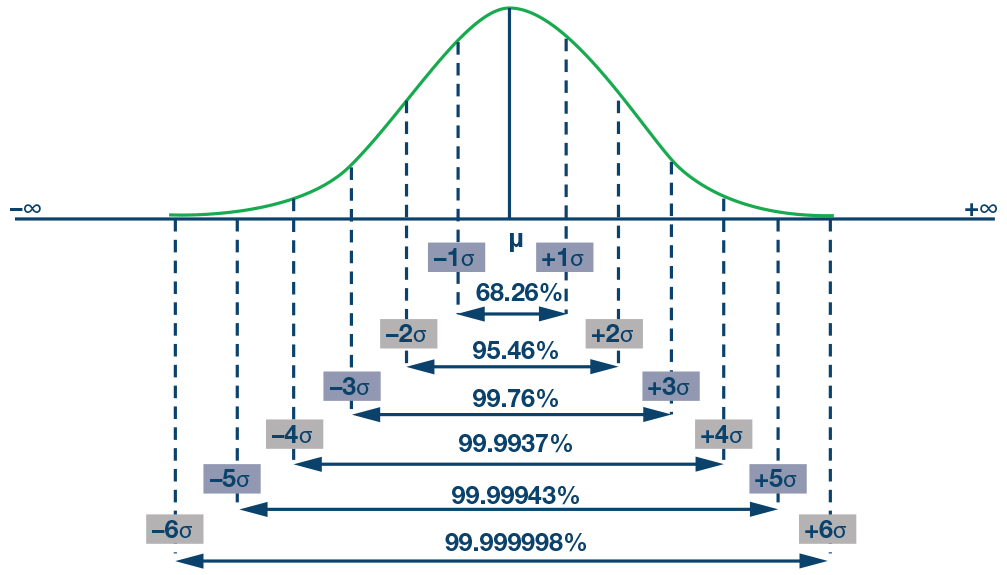
图 11.高斯分布曲线,包括西格玛水平 1 到 6。
从理论上讲,乘以均方根噪声的因子将决定算法生命周期内的失效时间,因为噪声是随时间推移的随机变量。但是,虽然噪声是不可预测的,但它可以通过统计计算。
假设 EPB 模块的算法的预期运行时间为 146,000(即,20 年内每天 20 次)。如果在其生存期内不允许发生故障,则最大故障率为 1/146,000 = 0.00068%。
根据高斯分布的西格玛水平(图 11),6 的西格玛水平产生 0.00034% 的缺陷百分比。因此,选择 6 作为均方根乘法因子对应于 146,000 × 0.00034% = 0.5 < 1。这意味着从统计上讲,EPB 模块在 20 年的使用寿命内不会发生任何故障。
我们可以将其总结为:
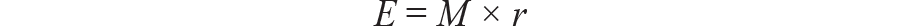
E 是生命周期内超过最坏情况的预期次数,M 是生命周期运行时间,r 是超过最坏情况的概率。基于此,我们可以通过乘以均方根噪声来评估一个合理的因素。
总结
以ADI公司的ADXC1500/ADXC1501(陀螺仪和2轴/3轴加速度计组合)为例,表1列出了所有误差贡献项目,有或没有校准措施。我们可以假设总偏移变化为 2德·曲线和温度变化占其总失调变化的80%。另外,取6作为因子乘以最大均方根噪声。
陀螺仪和三轴加速度计的这种组合可实现许多新应用,特别是在汽车安全系统和工业自动化应用中。最大限度地减少这些大误差源对于设计更可靠、更准确的汽车安全系统(如稳健的电子稳定控制 (ESC) 和翻车检测)至关重要。这些建立在车辆中已有的传统底盘控制系统之上,包括防抱死制动系统、牵引力控制和偏航控制。
审核编辑:郭婷
-
芯片
+关注
关注
455文章
50711浏览量
423103 -
陀螺仪
+关注
关注
44文章
783浏览量
98660 -
加速度计
+关注
关注
6文章
699浏览量
45891
发布评论请先 登录
相关推荐
加速度计提高倾角测量精度的方法
基于加速度计的倾角测量精度提高
Mems加速度计对于温度测量是准确
2476-100加速度计
2227-050加速度计模块
1410L-100加速度计
1521L-200加速度计
基于MEMS加速度计实现动态倾角测量系统的设计
倾角测量精度怎么提高?不妨用加速度计试试资料下载





 如何使用加速度计提高倾角测量的准确性
如何使用加速度计提高倾角测量的准确性










评论