什么是深度学习中优化算法
先大致讲一下什么是深度学习中优化算法吧，我们可以把模型比作函数，一种很复杂的函数：h(f(g(k(x))))，函数有参数，这些参数是未知的，深度学习中的“学习”就是通过训练数据求解这些未知的参数。
由于这个函数太复杂了，没办法进行直接求解，所以只能换个思路：衡量模型的输出与真实标签之间的差距，如果差距过大，则调整模型参数，然后重新计算差距，如此反复迭代，直至差距在接受范围内。
深度学习中通过目标函数或者损失函数衡量当前参数的好坏，而调整模型参数的就是优化算法。
所谓优化， 就是利用关于最优解的信息，不断逼近最优解， 目前深度学习中最常用的是梯度下降法， 梯度方向就是最优解的信息，因为梯度方向指向最优解方向， 沿着梯度方向前进即可靠近最优解。
到这里，你是不是觉得优化算法很简单？其实，不然。让我们进一步分析。
难点一：梯度（困难指数两颗星）
所谓梯度下降法，当然要计算梯度，前面那个复合函数再加上损失函数，最终要优化的函数是这个样子：L(h(f(g(k(x)))),y)，L是损失函数，y是标签值。
复合函数通过链式法则进行求导，例如f(g(x))，
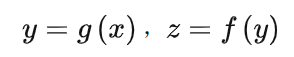
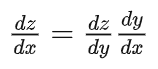
这就要求g(x)和f(x)都得可导，对于神经网络而言，卷积层和全连接层都可以看作是矩阵与向量乘法，是可导的，剩下的就是激活函数和损失函数，好在目前常用的MSE，交叉熵损失函数，Sigmoid，Relu激活函数都是可导的。
所以，梯度的问题不大。
难点二：凸优化和非凸优化（ 困难指数五颗星 ）
深度学习由于多个隐藏层的叠加所形成的复合函数，外加损失函数，最终的函数往往不是凸函数。
所谓凸函数，就是只有全局最优解，通过梯度下降最终都能找到这个最优解，对于机器学习中的线性回归的损失函数：最小二乘而言，它是一个凸函数，也就是说能找到使损失函数达到最小值的全局最优解。
在非凸函数中，存在大量的局部最优解，局部极值随着特征维度的增加呈指数增长，优化算法很大概率找不到全局最优解，这也是优化算法最苦恼的地方。
如果只有局部最优解，那情况还不算最糟糕，毕竟局部最优解意味着从所有维度看都是最小值或者最大值，更糟糕的是鞍点，这种情况虽然一阶导数都为零，但二阶导数不同向，也就是说从某些维度看是极小值，而从某些维度看却是极大值。
而且，不幸的是，随着特征向量维度的增加，鞍点的数量也是随着指数级增加的。
那如何逃离鞍点？
这里再次注意：这里我们所说的梯度下降指的是：使用全部样本的损失的平均值来更新参数，这就意味着梯度的精度非常高，会精确地逼近鞍点，但我们不希望这样，我们希望能够跳出鞍点，幸好，随机梯度下降SGD或者其变体（比如Momentun、Adam、mini-batch）的出现很大程度上解决了该问题。
例如，mini-batch是指每次参数更新只是用一小批样本，这是一种有噪声的梯度估计，哪怕我们位于梯度为0的点，也经常在某个mini-batch下的估计把它估计偏了，导致往前或者往后挪了一步摔下马鞍，也就是mini-batch的梯度下降法使得模型很容易逃离特征空间中的鞍点。
既然，局部极值点也可接受，且又能有方法逃离鞍点，到这里你觉得问题就结束了吗？还没有，其实，神经网络中最让人望而生畏的不是局部最优点和鞍点，而是平坦地区，这些地区一经进入很难逃离。
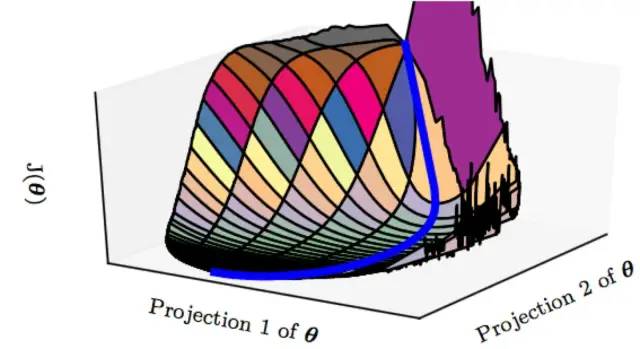
总结来说，人们认为的深度神经网络“容易收敛到局部最优”，很可能是一种想象，实际情况是，我们可能从来没有找到过“局部最优”，更别说全局最优了。
所以，与其担忧陷入局部最优点怎么跳出来，更不如去考虑数据集要怎么做才能让网络更好学习，以及网络该怎么设计才能更好的捕获pattern，网络该怎么训练才能学到我们想让它学习的知识。
最后，也要为优化算法鸣个不平。其实这并不是优化算法的问题。是损失函数和网络结构的错，是他们的复杂性导致优化问题是一个非凸优化问题，优化算是是来解决问题的，而不是制造问题。
-
优化算法
+关注
关注
0文章
35浏览量
9679 -
函数
+关注
关注
3文章
4327浏览量
62567 -
深度学习
+关注
关注
73文章
5500浏览量
121109
发布评论请先 登录
相关推荐
深度学习算法进行优化的处理器——NPU
PyTorch教程-12.1. 优化和深度学习
工商网监
评论