***11 ***训练神经网络 第二部分
现在我们有了一个明确的目标:最小化神经网络的损失。通过调整网络的权重和截距项,我们可以改变其预测结果,但如何才能逐步地减少损失?
这一段内容涉及到多元微积分,如果不熟悉微积分的话,可以跳过这些数学内容。
为了简化问题,假设我们的数据集中只有Alice:
假设我们的网络总是输出0,换言之就是认为所有人都是男性。损失如何?

那均方差损失就只是Alice的方差:
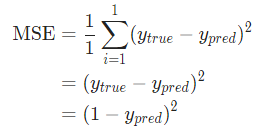
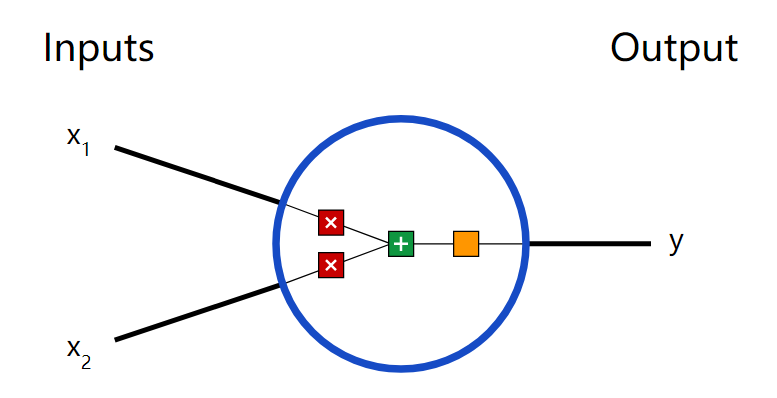
也可以把损失看成是权重和截距项的函数。让我们给网络标上权重和截距项:
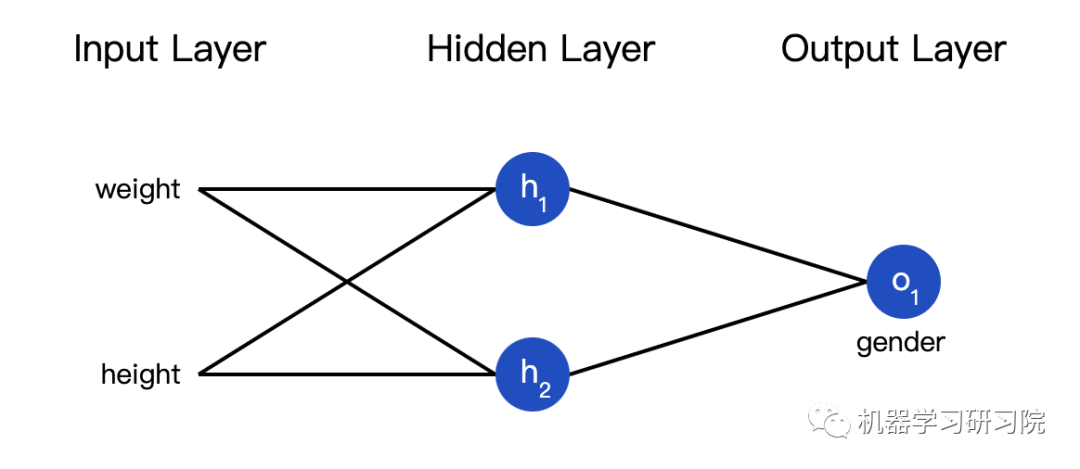
这样我们就可以把网络的损失表示为:
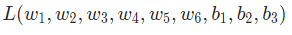
假设我们要优化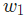 ,当我们改变
,当我们改变 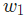 时,损失
时,损失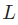 会怎么变化?可以用
会怎么变化?可以用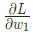 来回答这个问题,怎么计算?
来回答这个问题,怎么计算?
接下来的数据稍微有点复杂,别担心,准备好纸和笔。
首先,让我们用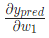 来改写这个偏导数:
来改写这个偏导数:
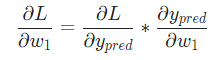
因为我们已经知道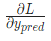 ,所以我们可以计算
,所以我们可以计算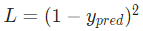
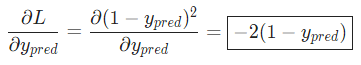
现在让我们来搞定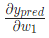 。
。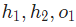 分别是其所表示的神经元的输出,我们有:
分别是其所表示的神经元的输出,我们有:
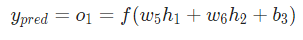
由于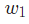 只会影响
只会影响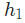 (不会影响
(不会影响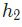 ),所以:
),所以:
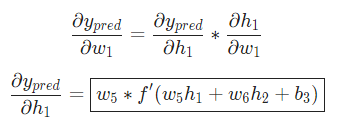
对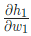 ,我们也可以这么做:
,我们也可以这么做:
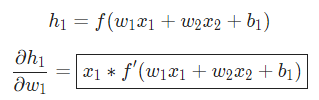
在这里,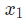 是身高,
是身高,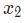 是体重。这是我们第二次看到
是体重。这是我们第二次看到 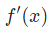 (S型函数的导数)了。求解:
(S型函数的导数)了。求解:
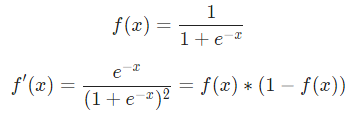
稍后我们会用到这个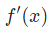 。
。
我们已经把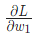 分解成了几个我们能计算的部分:
分解成了几个我们能计算的部分:
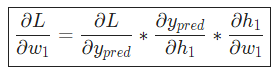
这种计算偏导的方法叫『反向传播算法』(backpropagation)。
好多数学符号,如果你还没搞明白的话,我们来看一个实际例子。
***12 ***例子:计算偏导数
我们还是看数据集中只有Alice的情况:

把所有的权重和截距项都分别初始化为1和0。在网络中做前馈计算:
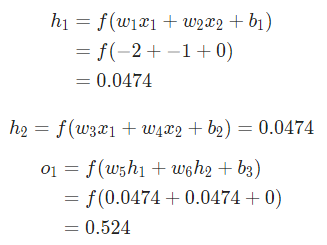
网络的输出是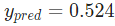 ,对于Male(0)或者Female(1)都没有太强的倾向性。算一下
,对于Male(0)或者Female(1)都没有太强的倾向性。算一下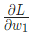
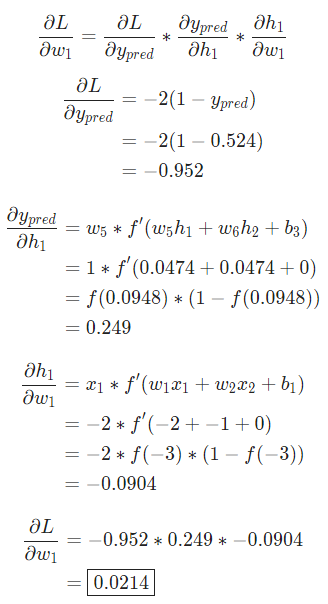
提示: 前面已经得到了S型激活函数的导数 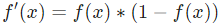 。
。
搞定!这个结果的意思就是增加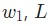 也会随之轻微上升。
也会随之轻微上升。
***13 ***训练:随机梯度下降
现在训练神经网络已经万事俱备了!我们会使用名为随机梯度下降法的优化算法来优化网络的权重和截距项,实现损失的最小化。核心就是这个更新等式:
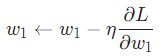
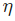 是一个常数,被称为学习率,用于调整训练的速度。我们要做的就是用
是一个常数,被称为学习率,用于调整训练的速度。我们要做的就是用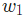 减去
减去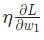
- 如果
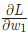 是正数,
是正数,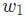 变小,
变小,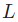 会下降。
会下降。 - 如果
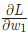 是负数,
是负数,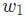 会变大,
会变大,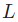 会上升。
会上升。
如果我们对网络中的每个权重和截距项都这样进行优化,损失就会不断下降,网络性能会不断上升。
我们的训练过程是这样的:
- 从我们的数据集中选择一个样本,用随机梯度下降法进行优化——每次我们都只针对一个样本进行优化;
- 计算每个权重或截距项对损失的偏导(例如
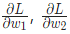 等);
等); - 用更新等式更新每个权重和截距项;
- 重复第一步;
-
神经网络
+关注
关注
42文章
4771浏览量
100704 -
神经元
+关注
关注
1文章
363浏览量
18449 -
python
+关注
关注
56文章
4792浏览量
84623
发布评论请先 登录
相关推荐
labview BP神经网络的实现
【PYNQ-Z2试用体验】神经网络基础知识
卷积神经网络如何使用
【案例分享】ART神经网络与SOM神经网络
人工神经网络实现方法有哪些?
如何构建神经网络?
基于BP神经网络的PID控制
卷积神经网络一维卷积的处理过程
用Python从头实现一个神经网络来理解神经网络的原理1
用Python从头实现一个神经网络来理解神经网络的原理2
用Python从头实现一个神经网络来理解神经网络的原理4





 用Python从头实现一个神经网络来理解神经网络的原理3
用Python从头实现一个神经网络来理解神经网络的原理3
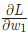 是正数,
是正数,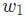 变小,
变小,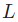 会下降。
会下降。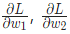 等);
等);









评论