本节将详细讲解椭圆函数滤波器(Elliptic Function Filter/Cauer Filter)的综合设计, 结合之前电路仿真的工作, 现将Elliptic滤波器集成到了滤波器设计App中, 提供一个试用版本, 并提供GitHub开源链接。
椭圆函数滤波器特点和用途
椭圆函数滤波器(Elliptic Function Filter或Cauer Filter, 在微波射频中有时也称作Achieser-Zolotarev滤波器)是Cauer于1930-1931年首先使用椭圆有理函数(Elliptic Rational Function)逼近来进行设计的滤波器, 其特点是通带和阻带内都具有等纹波特性, 对比Chebyshev滤波器其更具陡峭的截止特性, 被广泛用于实际工程应用之中, 比如在DDS输出级一般会加一个椭圆函数滤波器滤除镜像频率分量, 但是其缺点是对器件值要求非常苛刻(指精度和Q值), 很多滤波器理论上可行, 但是在实际中很难实现。
实际上椭圆函数滤波器的阻带纹波为零则表现为切比雪夫滤波器(Chebyshev I Filter)特性, 当通带纹波为0则表现为逆切比雪夫滤波器(Chebyshev II Filter)特性, 当通带和阻带纹波均为0则表现为巴特沃斯滤波器(Butterworth Filter)特性, 椭圆函数滤波器可以说是滤波器的终极存在。
椭圆函数滤波器逼近
如何由通带和阻带等纹波推导出椭圆函数特征多项式(2)请参考《滤波器设计的逼近方法 - Butterworth, Chebyshev, Elliptic》。
椭圆函数滤波器传递函数
椭圆函数滤波器的幅频响应传递函数为:
椭圆函数滤波器传递函数是从其定义推导而来, 即从通带和阻带都等纹波出发, 推导出椭圆函数滤波器的特征函数表达式满足如下关系:
式中是雅可比椭圆函数,即通带频率和阻带频率的比值,即通带纹波和阻带纹波的比值(注意这里纹波是线性坐标下的值,), 其中和由阶方程(degree equation)联系:
可以看到这个公式(2)和切比雪夫多项式
类比具有相同的形式, 实际上切比雪夫滤波器就是椭圆函数滤波器的特殊情况, 即当阻带纹波无穷大和阻带频率无穷大的特殊情况。
同样的当的通带纹波为0, 且通带频率也为0, 即时, 可以得到逆切比雪夫滤波器。
当的通带纹波为0, 阻带纹波为无穷大, 且通带频率为0, 且阻带频率为无穷大, 也即时, 可以得到逆切比雪夫滤波器。
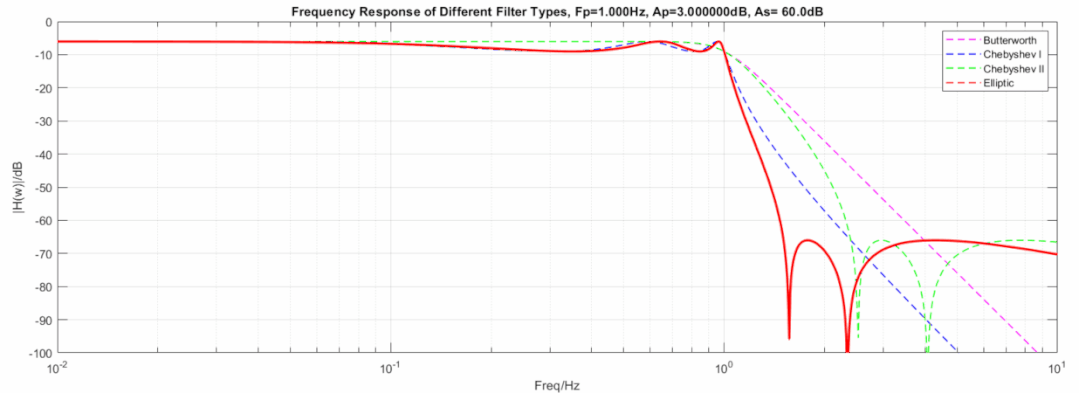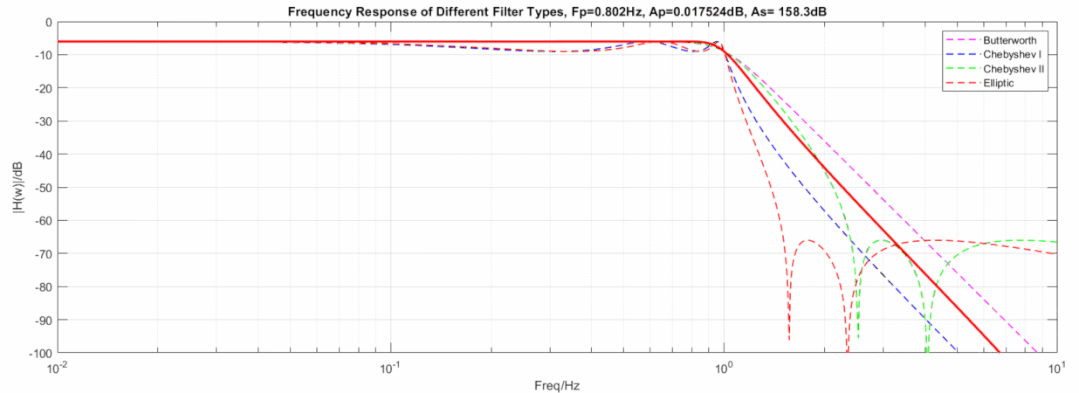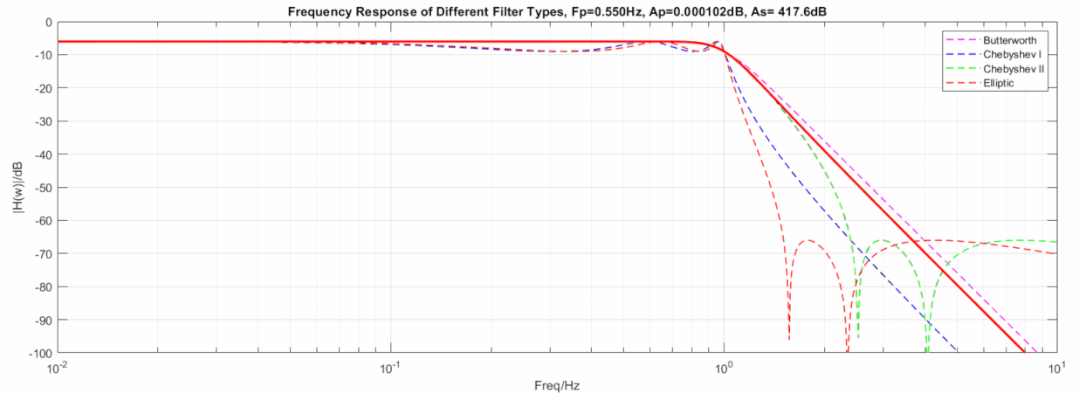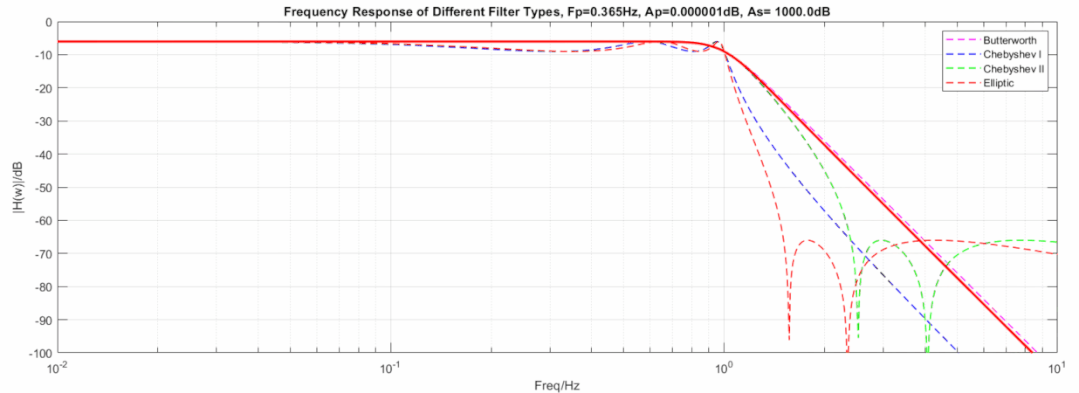
下图显示了三种滤波器在相同阶数, 相同截止频率下的动图展示:
椭圆到切比雪夫滤波器,从60dB变到1000dB动图:
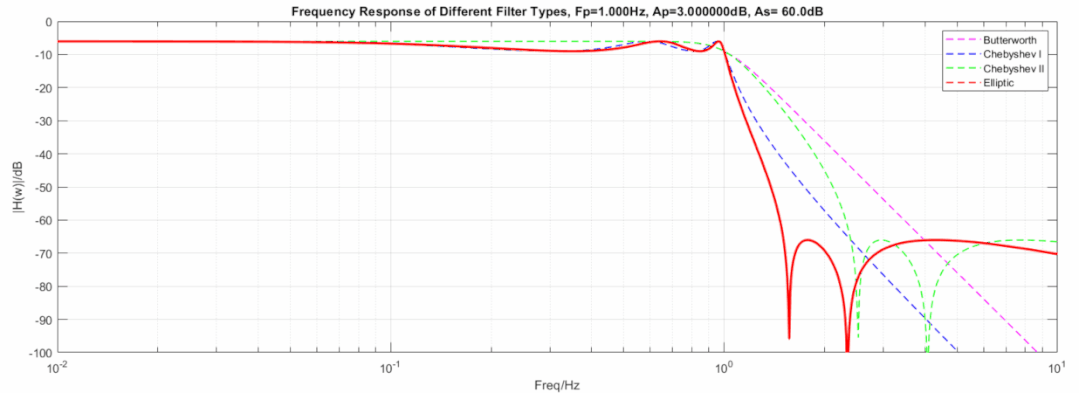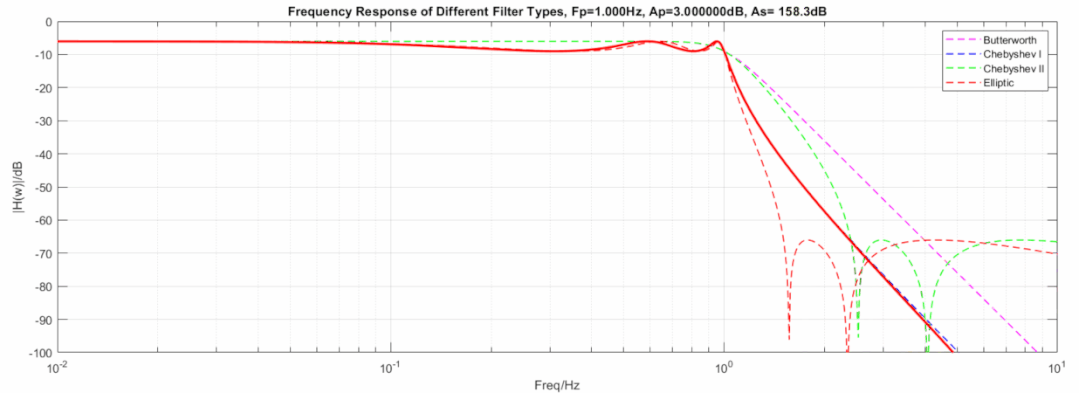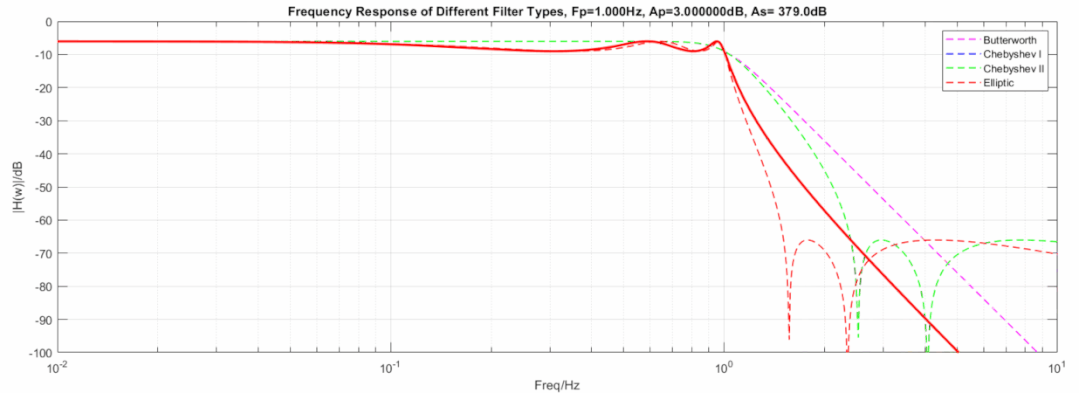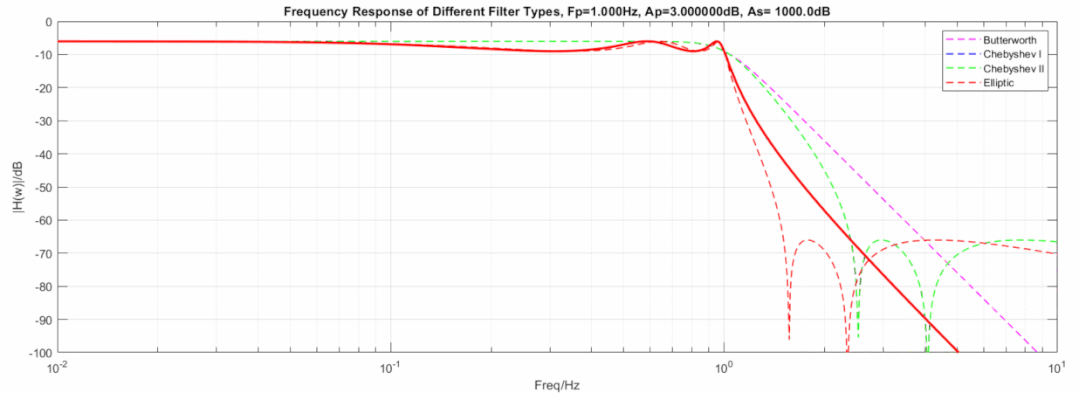
椭圆到逆切比雪夫滤波器,从3dB变到0.000001dB动图:
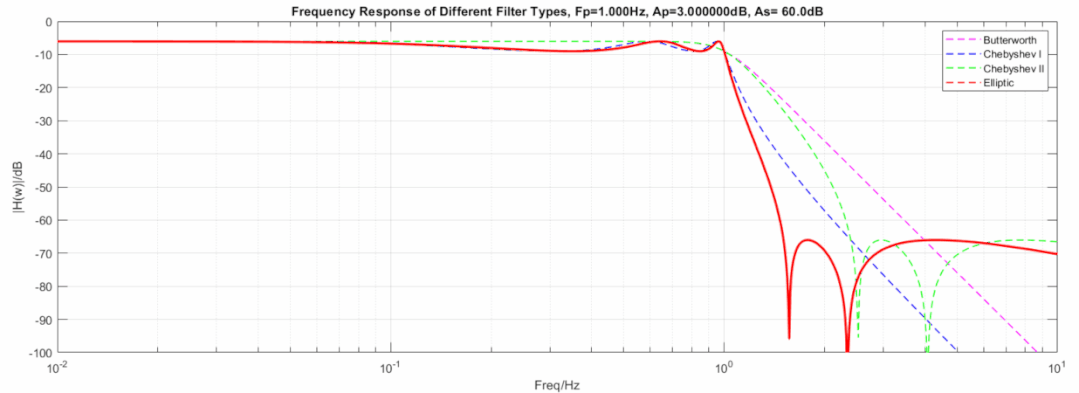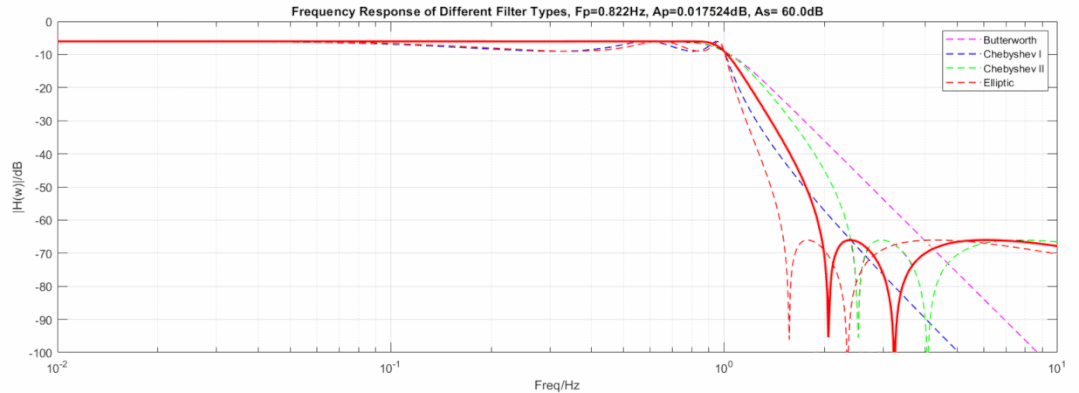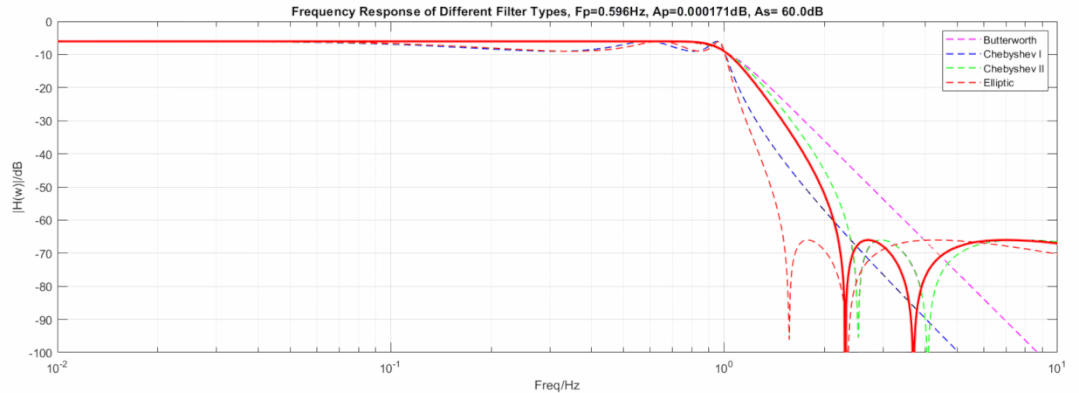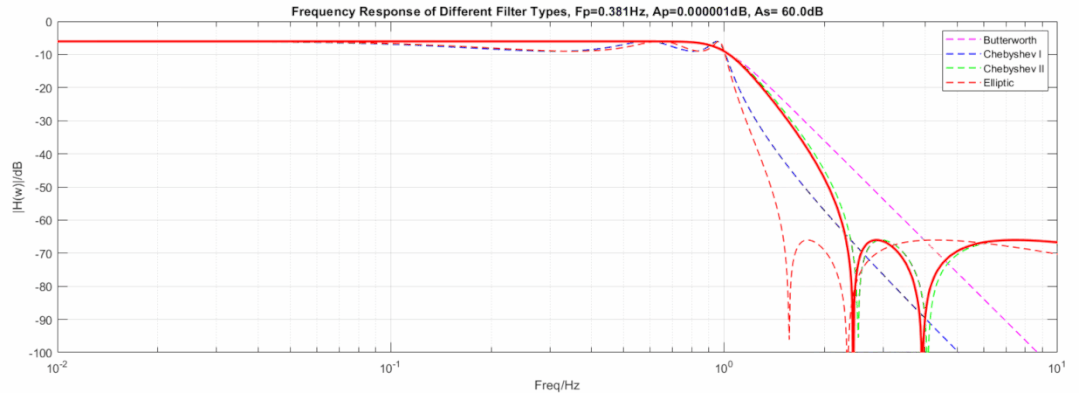
椭圆到巴特沃斯滤波器,从60dB变到1000dB且从3dB变到0.000001dB动图:
椭圆函数滤波器的零极点
椭圆函数滤波器的极点可以通过求解传递函数分母为0求解:
其中,是滤波器阶数。椭圆函数滤波器的零点和的极点相同, 这也比较容易理解, 设, 代入频率响应表达式, 通分后得到其零点和的一样, 在复平面中找到对应的极点位置得到:
滤波器零极点分析工具可以对各种不同滤波器进行零极点分析, 源码见, 下图是椭圆函数滤波器参数变化时滤波器的零极点和频响变化仿真结果:

下图是不同类型滤波器零极点对比图:
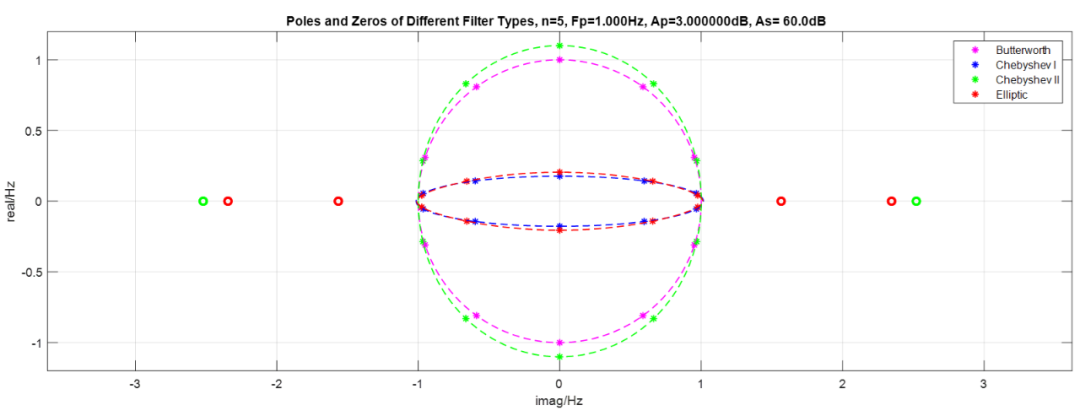
可见椭圆函数滤波器的极点形状不是一个椭圆, 所以之前的猜想并不正确, 椭圆函数滤波器得名并不是由于其极点形状是一个椭圆, 而是于其衰减特性可以由雅可比椭圆函数来描述。滤波器名称由特征函数决定, 可以看到以后讨论的贝塞尔滤波器、高斯滤波器、勒让德滤波器均是依据特征函数或传递函数来得名的。
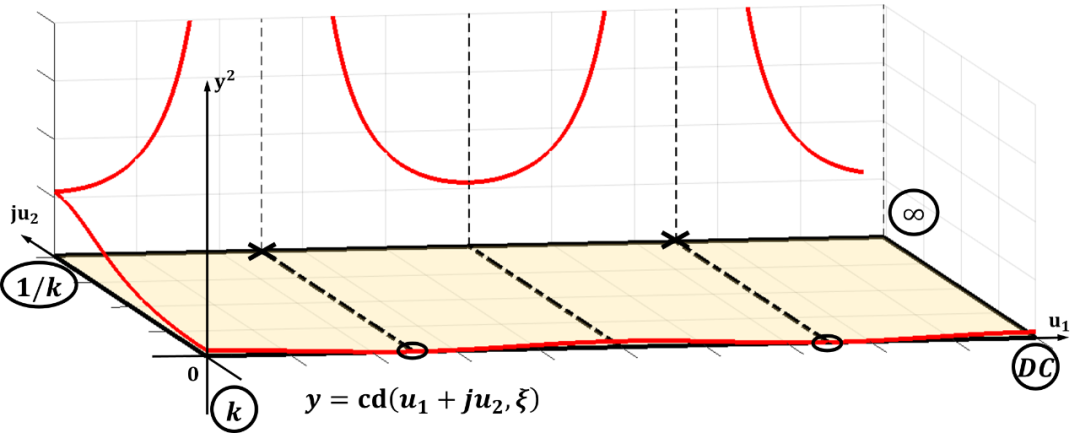
下图是滤波器在-平面的曲线图,从中可以看到4阶椭圆函数滤波器的零极点的分布情况(注意这个并不能直接通过电路综合,需要莫比乌斯变换后才能综合,见下文):
由衰减确定滤波器阶数
椭圆函数滤波器的参数由如下图所示(,):
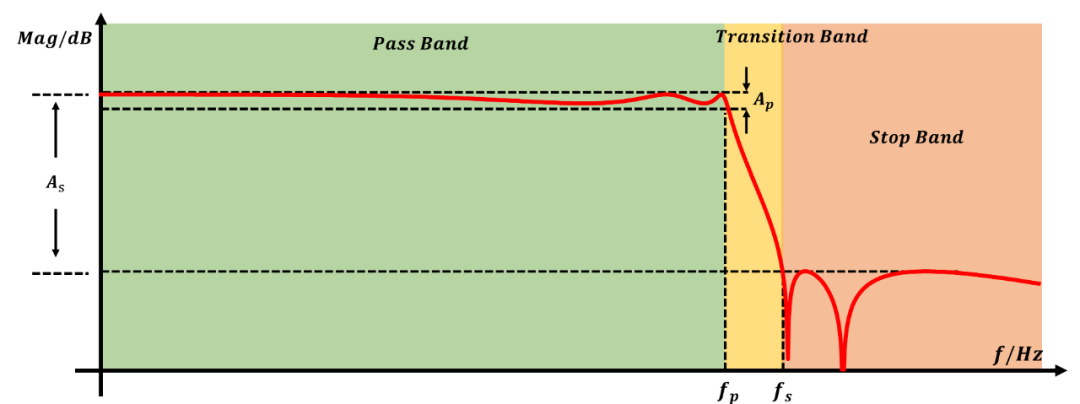
椭圆函数滤波器阶数和滤波器的衰减参数由阶方程决定, 阶方程将椭圆函数滤波器的阶数, 纹波以及通带阻带频率联系起来了, 其底层原理是由于在解椭圆积分方程中需要让虚部周期相同,实部周期呈整数倍,这样才能满足通带和阻带等纹波。阶方程的数值计算用到了兰登变换(Landen Transform,链接提供了多种计算方法), 现在有现成的迭代方法可以求解, Matlab中可以使用ellipdeg函数求解。
上式是已知通带阻带频率, 通带阻带纹波求阶数, 其值可能是个小数, 需要向上取整, 取整后还需要再使用一次阶方程求解出对应的值。
这里也给出阶方程的直接求解方法(也是雅可比所提出的模方程, Matlab中也使用了此算法):
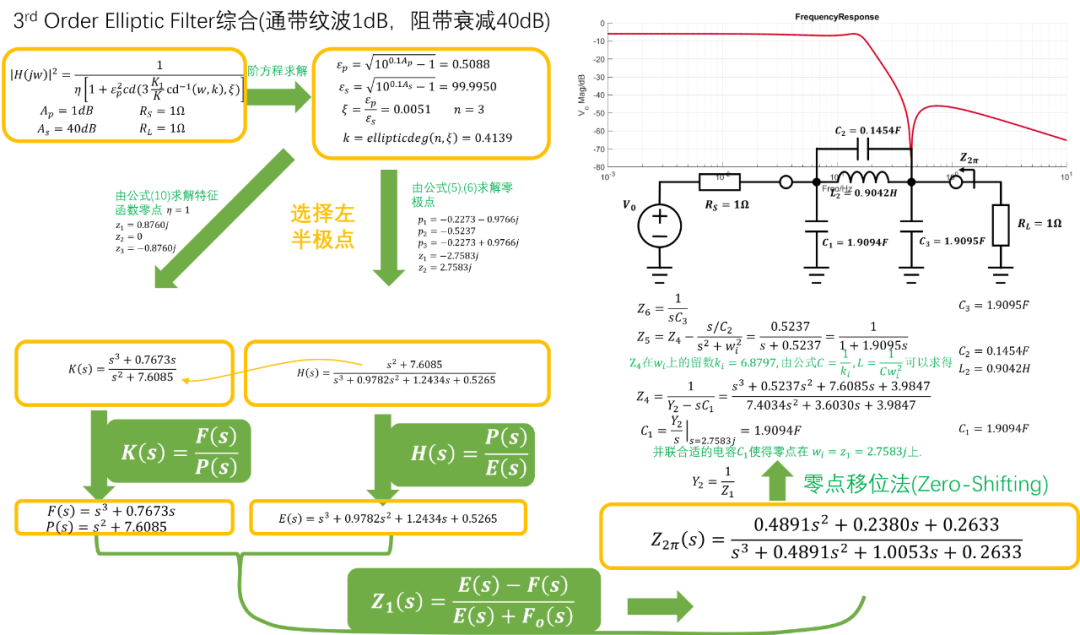
这里给出一个匹配型3阶椭圆函数滤波器设计实例:
非匹配型椭圆函数滤波器设计
非匹配型椭圆函数滤波器传递函数为:
其传递函数的零极点和匹配型滤波器的相同,不同的在于特征函数零点,依据特征函数定义,并令其等于0可以求得零点为:
其中为虚数,为雅可比椭圆反正弦函数,为通带纹波,为滤波器阶数,为增益因子, 和之前有效衰减一样:
通过以上求解可以得到计算出滤波器输入阻抗,同逆切比雪夫滤波器设计一样,由零点移除技术可以综合出所需要的电路网络。
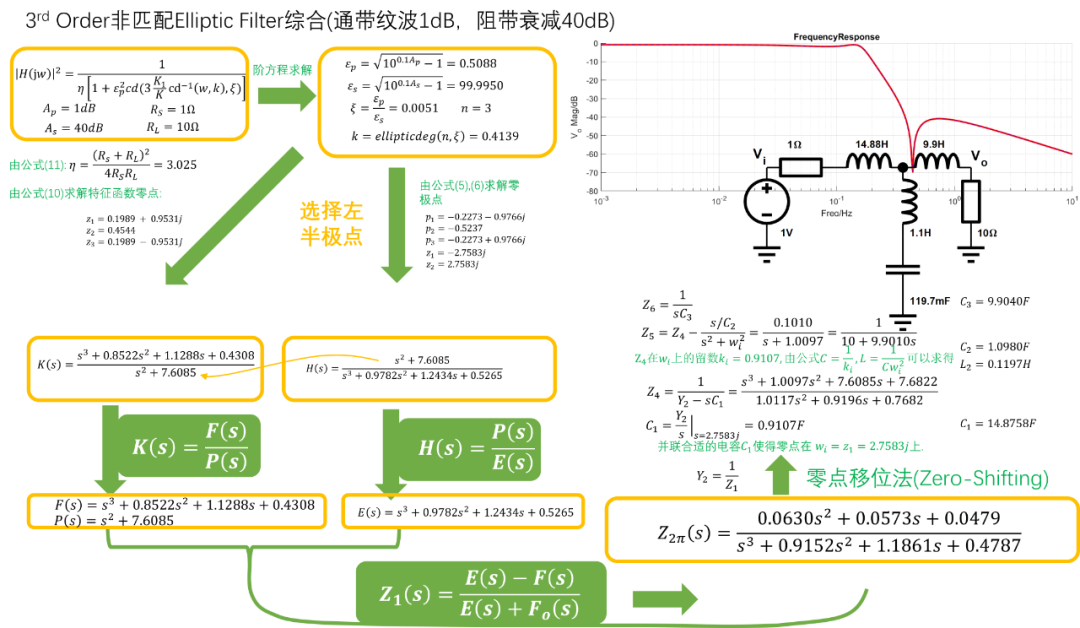
这里给出一个非匹配型3阶椭圆函数滤波器设计实例:
偶数阶椭圆函数滤波器设计
偶数阶椭圆函数滤波器为什么和奇数阶滤波器设计独立开来的原因与之前Chebyshev滤波器设计一样, 也是由于0频率处衰减有个和纹波一样的衰减, 以及无穷频率处衰减不为0所导致的, 解决此问题的办法就是使用频率变换, 即双线性变换(也称为莫比乌斯变换, Möbius transformation):
基本原则是:
当时,,是偶数阶椭圆函数滤波器的第一个纹波最高点位置所对应的频率。
当时,。
当时,,是偶数阶椭圆函数滤波器的最后一个零点位置所对应的频率。
通过以上条件得到:
其中:
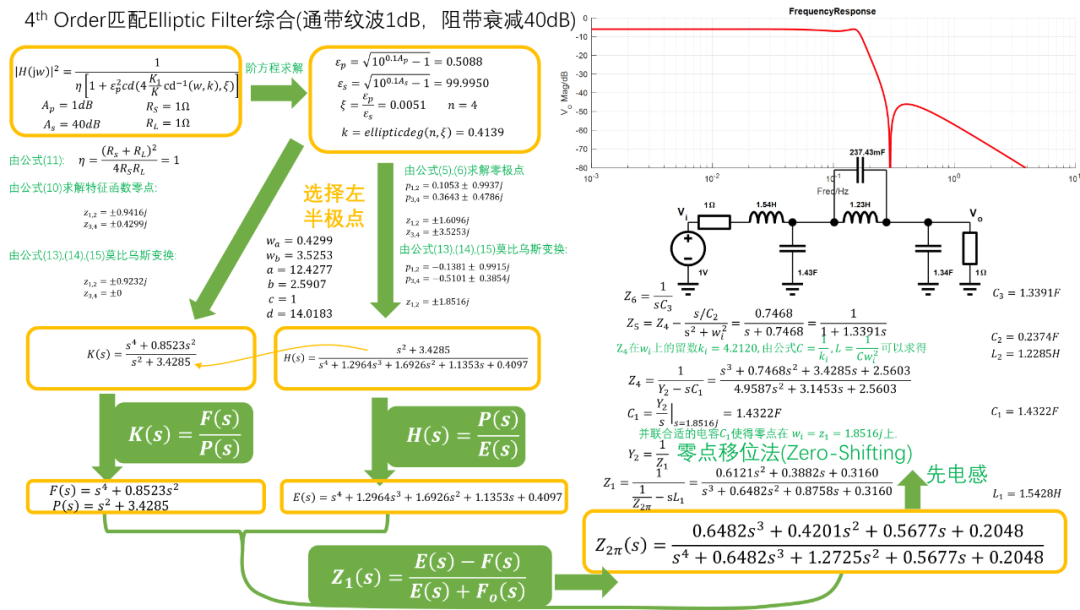
这里给出一个匹配型4阶椭圆函数滤波器设计实例:
不同滤波器通带类型之间的转换
只要有了低通原型, 其他滤波器通带类型之间的转换同Butterworth滤波器。
椭圆函数滤波器设计软件
基于Matlab的appdesign工具开发了一套椭圆函数滤波器设计软件,主要特点是:
支持椭圆函数滤波器(Elliptic Function Filter)、支持切比雪夫滤波器(Chebyshev I)、逆切比雪夫滤波器(Chebyshev II, Inverse Chebyshev)、巴特沃斯滤波器(Butterworth)设计
支持4种不同滤波器通带类型(LPF,HPF,BPF,BRF)设计
T型和PI型结构滤波器随意切换
可以设置阻带衰减决定滤波器阶数
可以设置通带衰减来综合滤波器
可以随意配置负载和终端阻抗, 并支持一端接载(源端电阻短路, 源端电流源, 终端开路, 终端短路)设计
可以幅频响应分析、零极点分析、瞬态分析
可以显示理想频率响应、零极点和实际仿真的的频率响应、零极点
可以支持实际标准器件逼近设计
Elliptic LPF设计举例
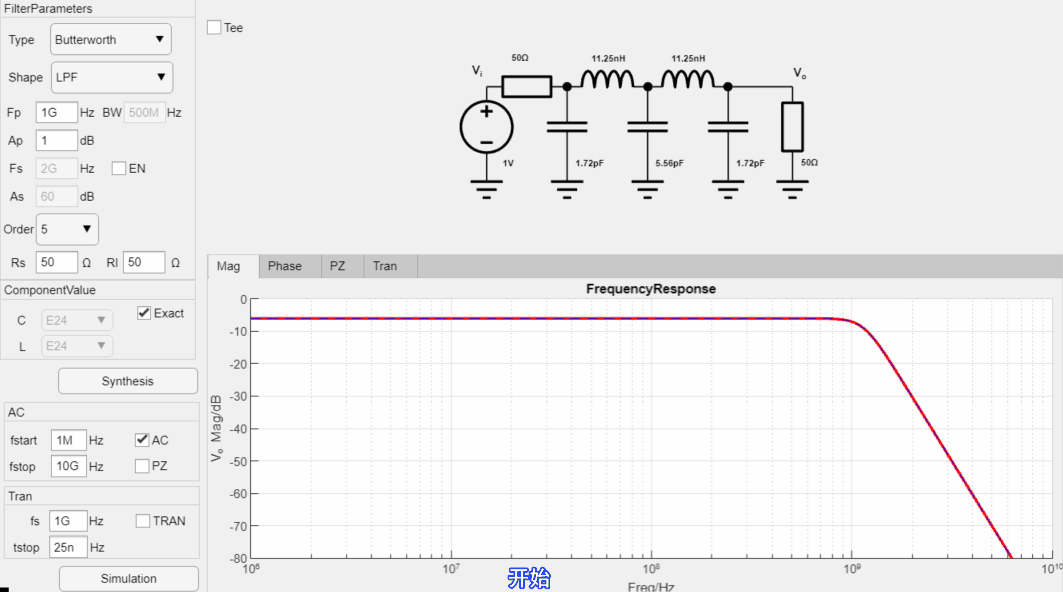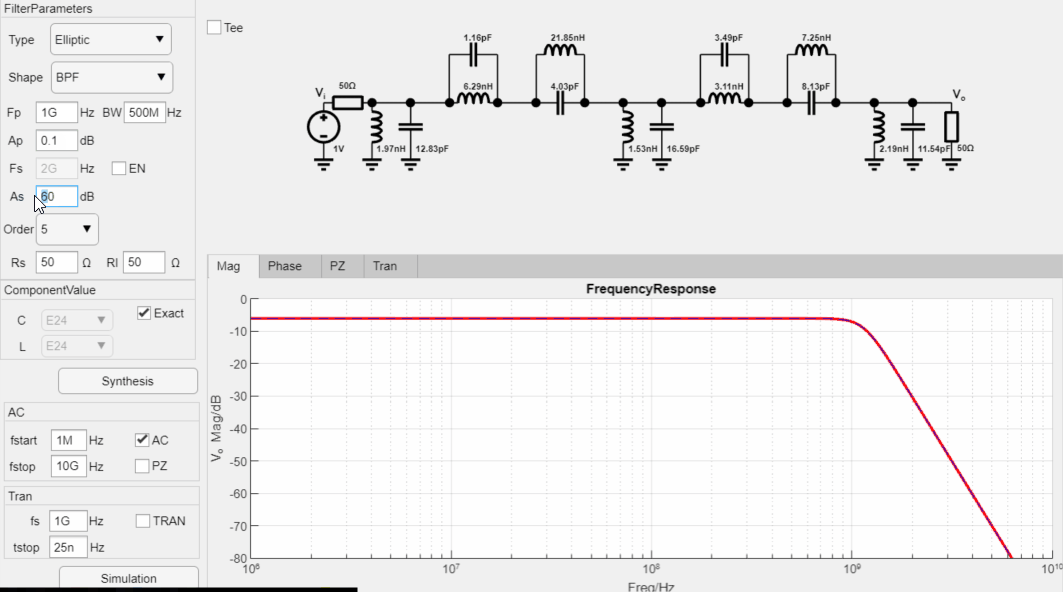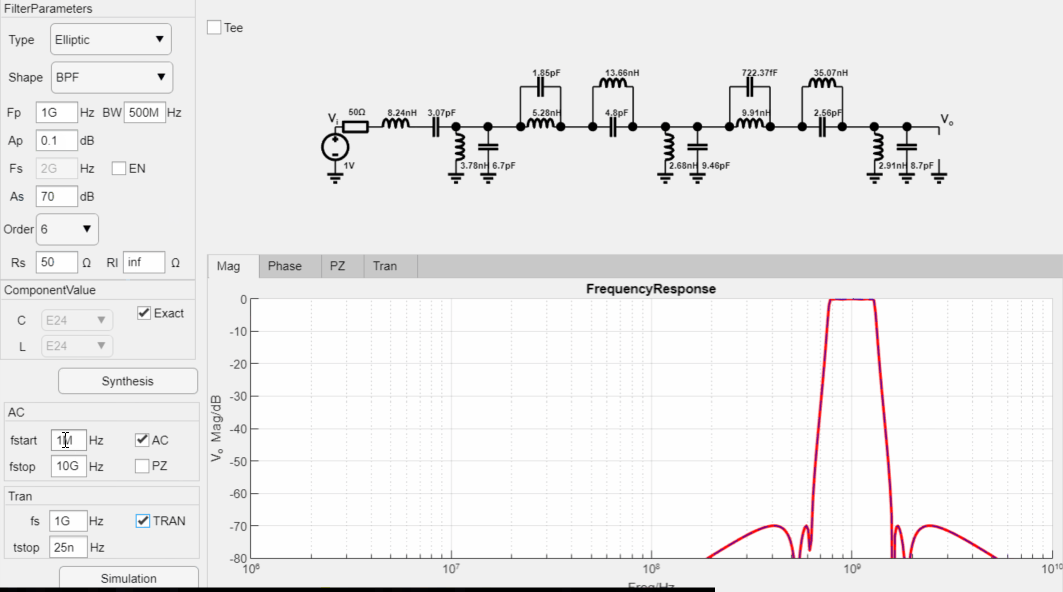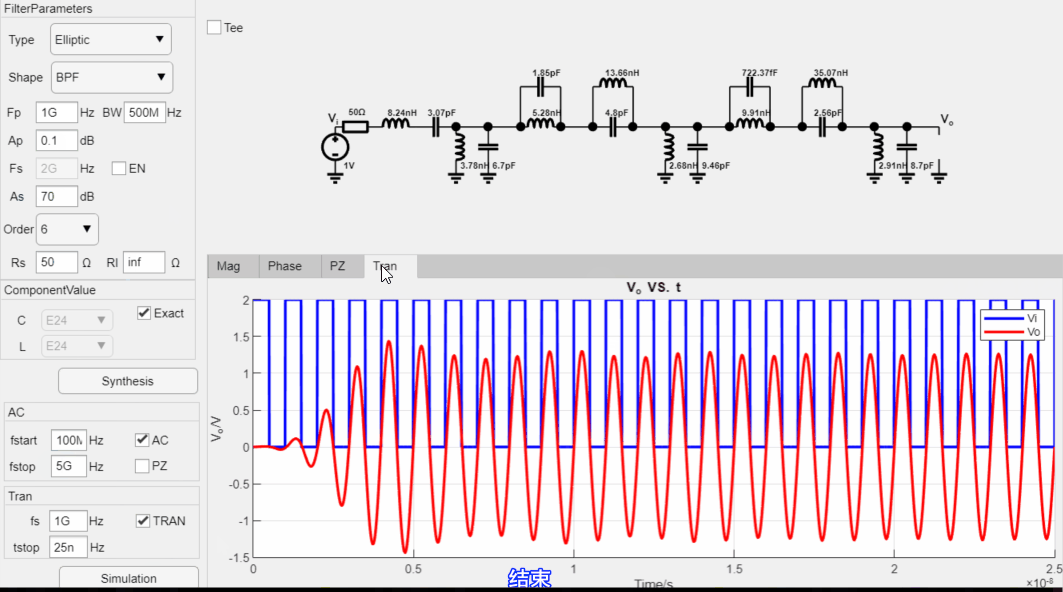
设计一款-3dB截止频率为1GHz,阻带纹波为60dB,通带纹波1dB的7阶低通Elliptic滤波器,输入输出阻抗为50欧姆,设计过程如下:
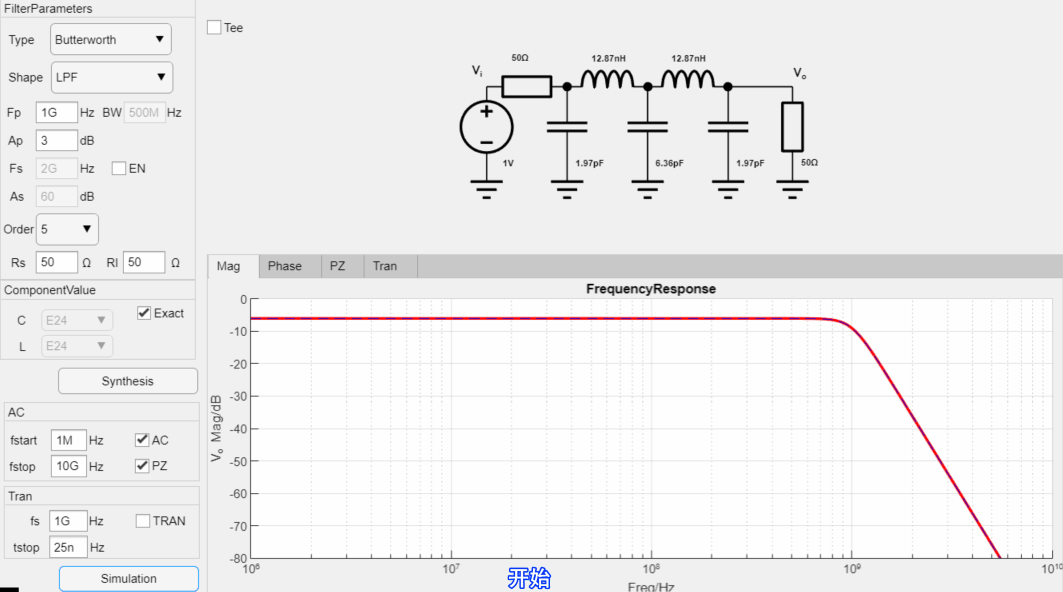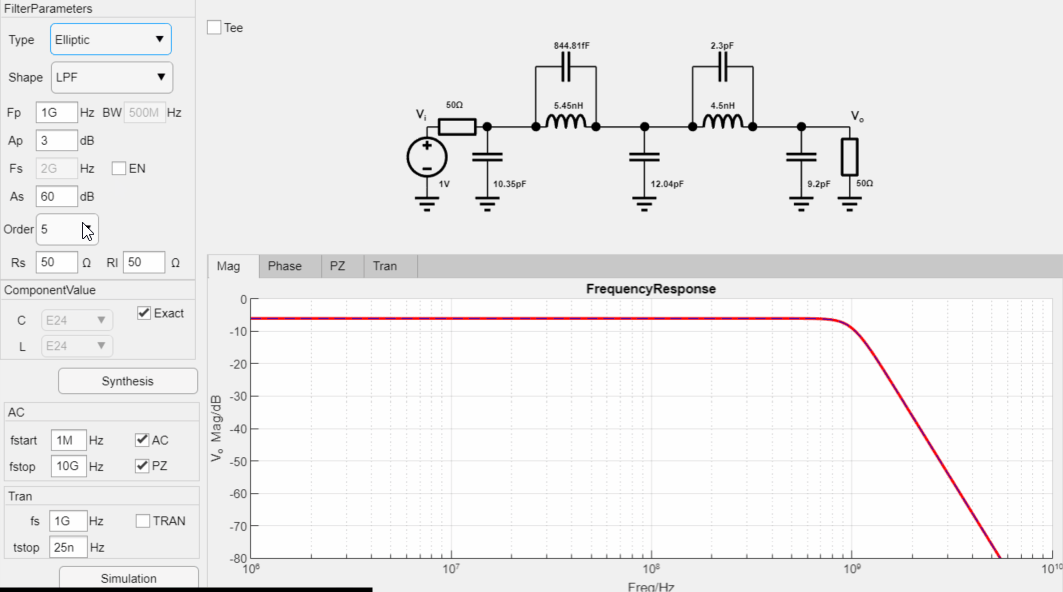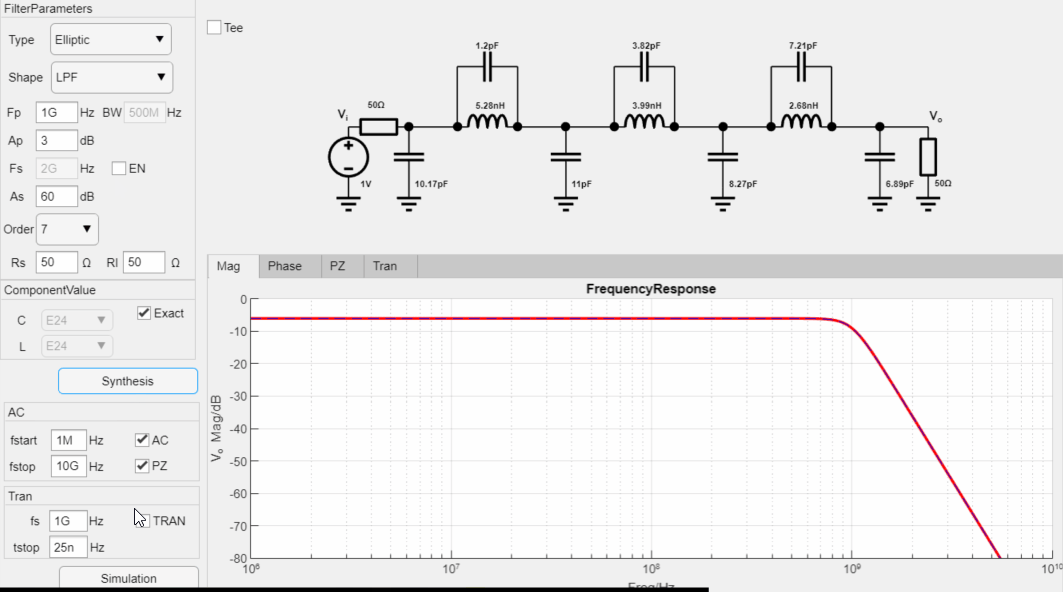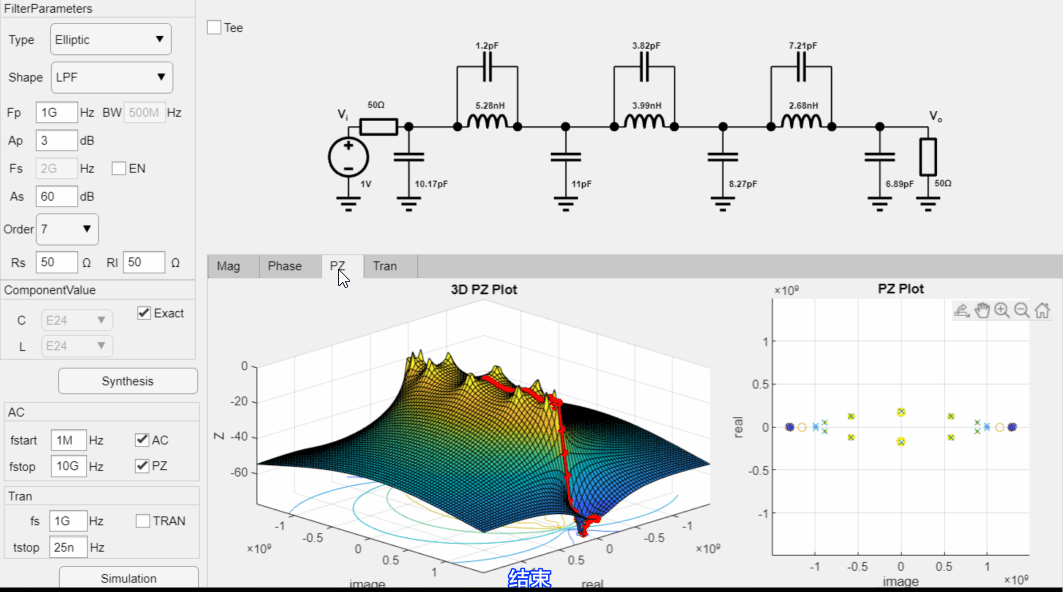
最终设计参数如下:
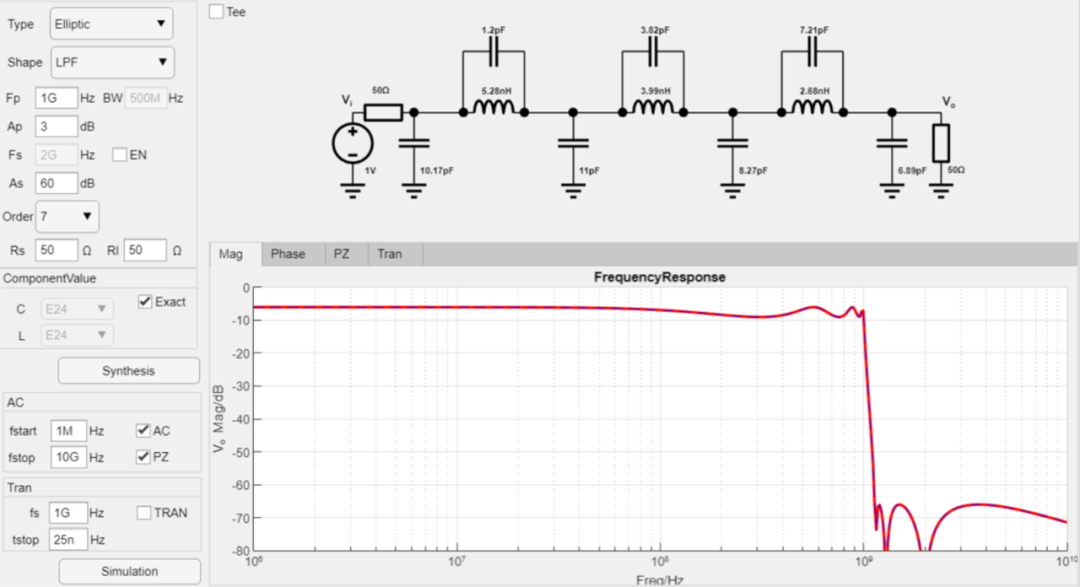
零极点仿真结果:
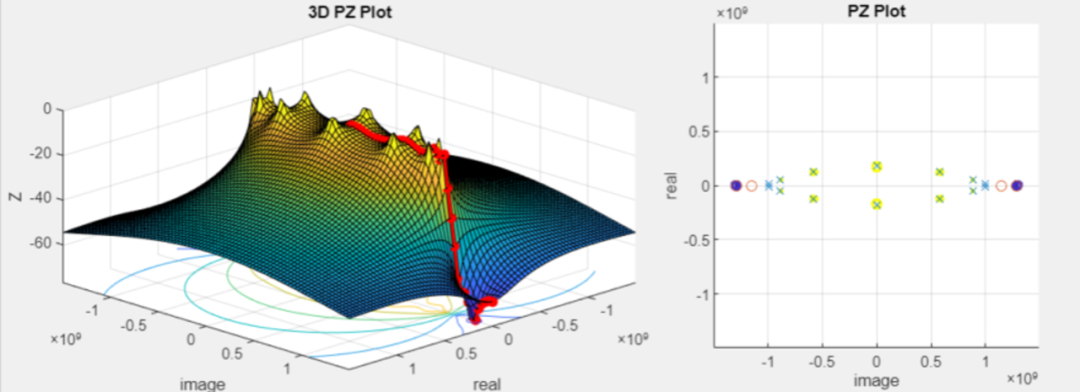
Elliptic BPF设计举例
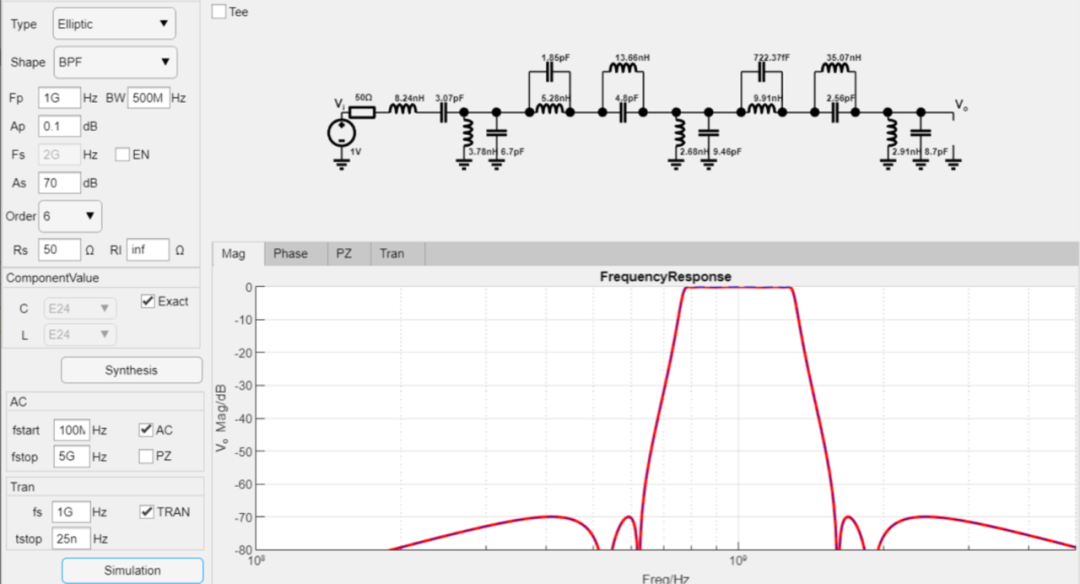
设计6阶带通Elliptic滤波器, 通带纹波为0.1dB, 阻带衰减为70dB, 中心频率为1GHz,带宽为500MHz,50欧姆输入,输出阻抗为高阻,最后进行瞬态仿真,设计过程如下:
最终设计参数如下:
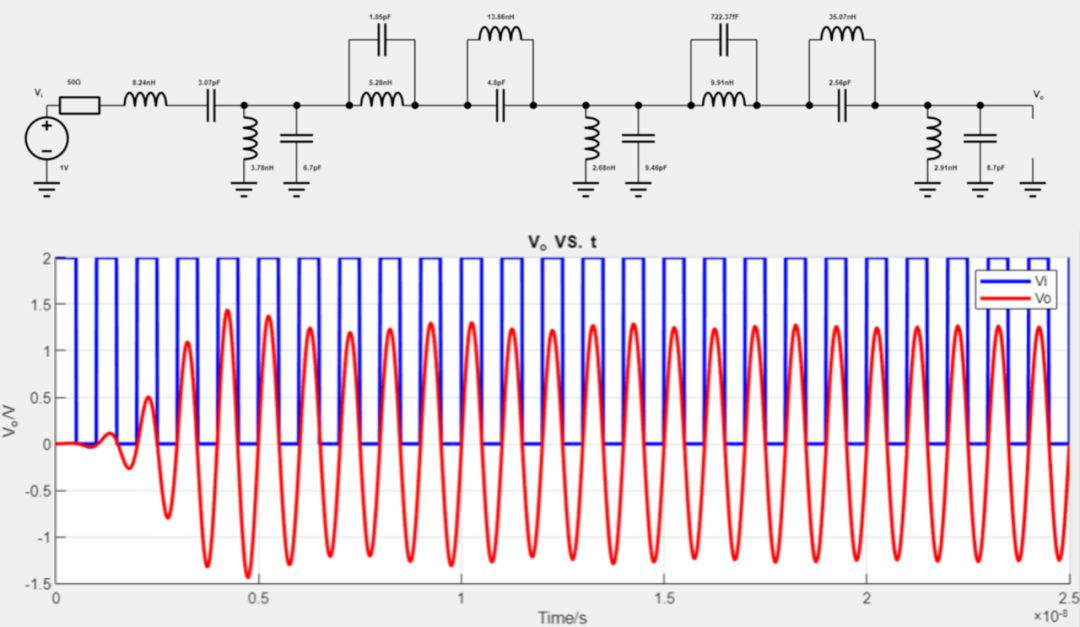
瞬态仿真结果:
程序的Matalb源码已经上传GitHub中(https://github.com/etools361/MatlabEllipticFilterDesignApp),有兴趣的同学可以下载试用体验,当然也欢迎技术交流。
审核编辑:汤梓红
-
滤波器
+关注
关注
161文章
7795浏览量
177990 -
电路仿真
+关注
关注
36文章
208浏览量
95679 -
函数
+关注
关注
3文章
4327浏览量
62569 -
传递函数
+关注
关注
0文章
102浏览量
13943 -
微波射频
+关注
关注
1文章
45浏览量
8746
原文标题:模拟无源滤波器设计(七)-Elliptic滤波器设计详解
文章出处:【微信号:电路设计小工具,微信公众号:电路设计小工具】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
全文详解IIR滤波器原理与设计方法

详解FIR滤波器和IIR滤波器的区别
详解FIR滤波器和IIR滤波器区别
滤波器有几种?四种滤波器之间对比详解
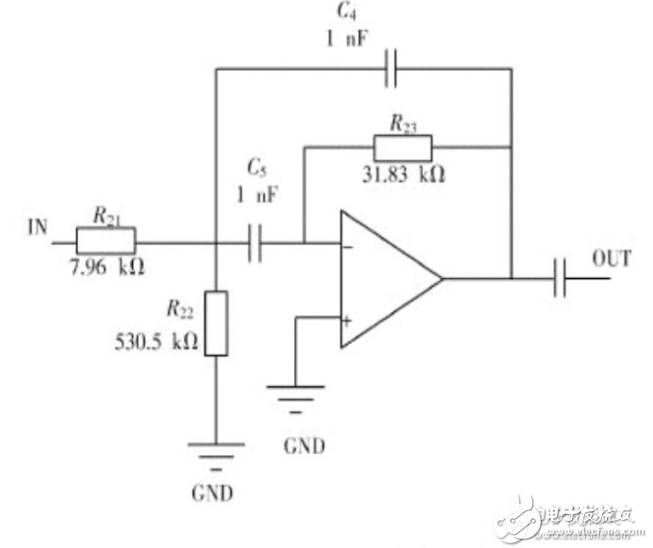
带通滤波器电路图大全(三款带通滤波器电路设计原理图详解)
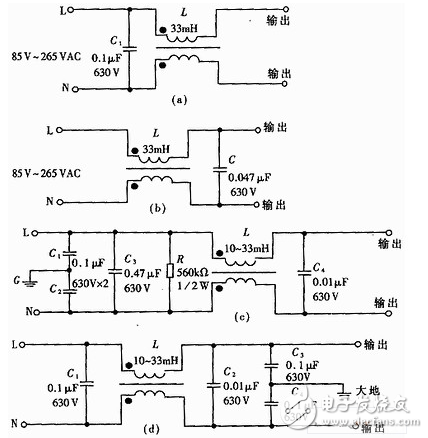
电源滤波器电路图大全(八款电源滤波器电路设计原理图详解)
220v电源滤波器电路图大全(五款220v电源滤波器电路设计原理图详解)
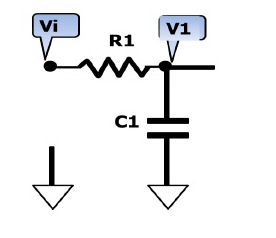
一文详解低通滤波器




 Elliptic滤波器设计详解
Elliptic滤波器设计详解










评论