机器学习笔记之高斯过程（上）
高斯分布
我们定义一个将输入x映射到输出y的函数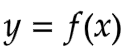
,在统计学中，我们使用随机模型来定义这种关系的概率分布。例如，一个3.8 GPA的学生可以获得平均$60K的薪水，方差（σ2）为$10K。
p(Salary=x|GPA=3.8)（一个均值为$60K，方差为$10k的高斯分布）
概率密度函数（Probability density function，PDF）
在下面的图表中，p(X=x) 服从高斯分布：
在高斯分布中，68%的数据在距离μ 1σ之内，95%的数据在距离μ 2σ之内。我们可以根据概率分布来进行数据采样。从分布
中采样数据的符号表示为：
在现实生活中，许多数据都遵循高斯分布。
例如，让我们建立旧金山居民身高和体重之间的关系模型。我们从1000名成年居民中收集信息，并将数据绘制如下图所示，每个红点代表1个人：
对应的三维概率密度函数（PDF）如下图所示：
让我们首先将模型推广到多元高斯分布，即概率密度函数取决于多个变量。
一个多元向量：
多元高斯分布的概率密度函数定义如下：
其中，Σ表示协方差矩阵：
让我们回到身高和体重的例子中，来说明这个公式的应用。
从我们的训练数据中，我们计算得到
=190，
=70：
协方差矩阵Σ是用来做什么的？协方差矩阵中的每个元素都代表着两个变量之间的关系。例如，
表示身高（
）与体重（
）的相关性。如果体重随身高的增加而增加，那么为正值。
让我们详细介绍如何计算上述的。为了简化，我们假设我们只有两个数据点（150磅，66英寸）和（200磅，72英寸）。
在计算了所有1000个数据之后，协方差矩阵Σ的值如下所示：
协方差矩阵Σ中的正元素值表示两个变量呈正相关关系。不出所料，是正值，因为体重随身高的增加而增加。如果两个变量彼此独立，则值应为0，如下所示：
计算
的概率
计算在给定
的条件下
的概率：
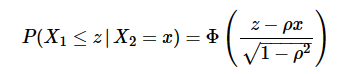
其中，Φ是累积分布函数（cumulative distribution function，CDF）：
我们将协方差变量Σ重写为以下形式：
代码
我们从一个二元高斯分布中采样数据。从协方差矩阵中，我们可以看出x和y呈正相关关系，因为
和
是正的。
mean = [0, 2]
cov = [[1, 2], [3, 1]]
x, y = np.random.multivariate_normal(mean, cov, 5000).T
plt.plot(x, y, 'x')
plt.axis('equal')
plt.show()
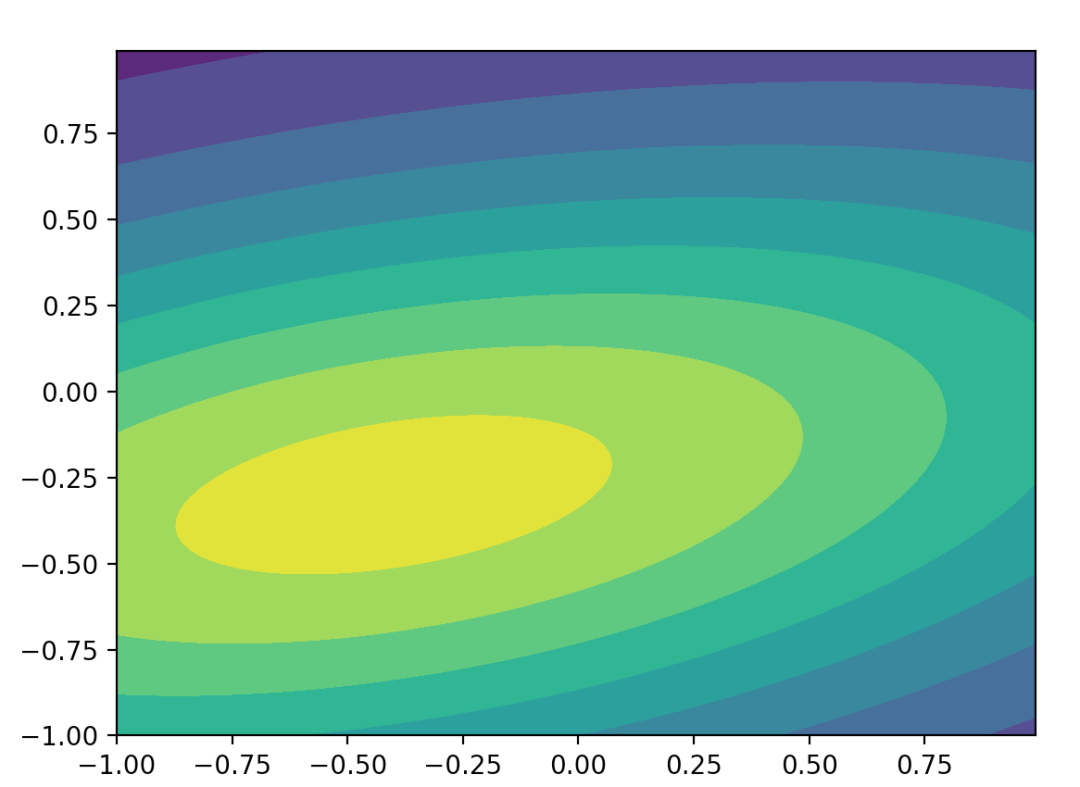
下面绘制（y,x）的概率分布图：
from scipy.stats import multivariate_normal
x, y = np.mgrid[-1:1:.01, -1:1:.01] # x (200, 200) y (200, 200)
pos = np.empty(x.shape + (2,))
pos[:, :, 0] = x; pos[:, :, 1] = y # pos (200, 200, 2)
mean = [-0.4, -0.3]
cov = [[2.1, 0.2], [0.4, 0.5]]
rv = multivariate_normal(mean, cov)
p = rv.pdf(pos) # (200, 200)
plt.contourf(x, y, p)
plt.show()
多元高斯分布定理
给定一个高斯分布：
后验条件概率
的计算公式如下所示。这个公式在后面的高斯过程中非常重要。例如，如果我们有1000个毕业生的GPA和薪水样本，我们可以使用这个定理通过1000个训练数据点创建一个高斯分布模型来预测给定GPA情况下的薪水P(salary|GPA)，
这里不详细介绍公式的推理过程。但是假设x服从高斯分布。和之间的相关性由μ和Σ定义。因此，给定的值，我们可以计算出的概率分布：p(|)。
例如，我们知道旧金山居民的身高服从高斯分布。在下一节中，我们将应用高斯过程来预测在给定身高的情况下体重的值。
高斯过程
高斯过程（Gaussian Process，GP）的直观理解很简单。如果两个点具有相似的输入，那么它们的输出也应该相似。对于有两个数据点的情况，如果一个数据点比另一个数据点更接近已知的训练数据点，那么它的预测结果会更加可靠。
例如，如果一个GPA为3.5的学生一年挣$70K，那么另一个GPA为3.45的学生应该会挣类似的薪水。在高斯过程中，我们使用训练数据集来构建高斯分布，以进行预测。对于每个预测，我们输出一个均值和一个σ。例如，使用高斯过程，我们可以预测一个GPA为3.3的学生可以挣到μ=$65K，σ=$5K，而一个GPA为2.5的学生可以挣到μ=$50K和σ=$15K。σ衡量了我们预测的不确定性。因为3.3 GPA更接近于我们的3.5 GPA训练数据，所以我们对于3.3 GPA学生的薪水预测比2.5 GPA学生更有信心。
在高斯过程中，我们不是计算Σ，而是计算K来衡量数据点
和
之间的相似性。
其中，核函数k是一个度量两个数据点相似性的函数（值为1表示相同）。有许多可能的核函数，我们将使用指数平方距离作为核函数。
注意：上面的表示数据点的体重。
表示数据点1。
有了所有的训练数据，我们可以创建一个高斯模型：
让我们再次用两个训练数据点（150磅，66英寸）和（200磅，72英寸）来演示。这里我们正在为我们的训练数据构建一个高斯模型。
其中175是体重的平均值，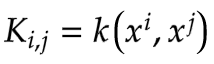
衡量了数据点和之间身高的相似性。上面的符号表示我们可以在体重上采样一个向量f。
从由数据点（150，66）和（200，72）建模的中进行采样。
现在假设我们要预测输入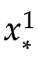
,
时的
,
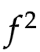。模型变为：
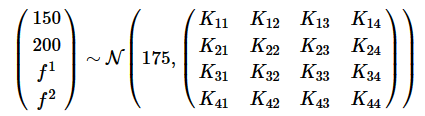
让我们再次理解一下这是什么意思。例如，我们有一个包含4个人身高的向量：
我们可以使用来采样这些人可能的体重：
我们知道前两个值来自训练数据，我们尝试计算出和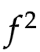的分布（它们的μ和σ是多少）。现在，我们不仅可以预测2个值，还可以对一系列输入值进行预测。
然后使用来采样向量：
例如，我们从中采样的第一个输出样本是：
-
函数
+关注
关注
3文章
4327浏览量
62567 -
随机
+关注
关注
0文章
12浏览量
9733 -
映射
+关注
关注
0文章
47浏览量
15811 -
高斯分布
+关注
关注
0文章
6浏览量
2750
发布评论请先 登录
相关推荐
高斯过程回归GPR和多任务高斯过程MTGP
基于高斯过程回归学习的频谱分配算法
什么是高斯过程 神经网络高斯过程解析
机器学习笔记之高斯过程（下）
PyTorch教程-18.1. 高斯过程简介
PyTorch教程-18.2. 高斯过程先验
PyTorch教程-18.3。高斯过程推理
工商网监
评论