基于Matlab/Simulink建立一种Thevenin/RC电池模块仿真模型-德赢Vwin官网网

本文以锂电池数学模型为基础，在Matlab/Simulink的仿真系统中，建立了一种Thevenin/RC电池模块仿真模型，通过实际工况试验，测试精度在允许误差范围内，为电池SOC/SOH研究提供了极大的参考价值。

1、等效电路模型参数辨识

锂电池在充放电结束后，端电压会迅速上升并逐渐趋向于一个稳定值，我们称之为锂电池的回弹特性。Thevenin/RC网络结构的工作特性通常满足回弹特性的特征，我们常用电池回弹阶段的电压、电流数据对Thevenin/RC模型进行参数辨识。

为辨识Thevenin/RC模型参数，需要获取电池在不同SOC状态下的电压回弹数据。首先采用恒流恒压的方法将电池充满，然后以1C的放电电流将电池SOC放至为0.9→0.1，得到每个时刻的电压回弹曲线。

具体的递推过程可以参考文献。（Schweighofer B , Raab K M , Brasseur G . Modeling of high power automotive batteries by the use of an automated test system[J]. IEEE Transactions on Instrumentation & Measurement, 2003, 52(4):1087-1091.）

最后，将每个SOC时刻的电压回弹数据进行拟合，可以得到电池模型参数随SOC的变化情况。

SOC = [0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1];
OCV_charge = [2.59 3.22 3.26 3.3 3.3 3.31 3.31 3.32 3.34 3.34 3.47];
OCV_discharge = [2.66 3.19 3.23 3.26 3.28 3.28 3.29 3.3 3.33 3.33 3.4];
R0_charge = [0.0306 0.0123 0.0126 0.012 0.0117 0.012 0.0117 0.0123 0.012 0.0144 0.0207];
R0_discharge = [0.0771 0.0168 0.0135 0.0123 0.0117 0.0123 0.0117 0.012 0.0117 0.0114 0.012];
R1_charge = [0.032155 0.008199 0.004763 0.004183 0.00348 0.003242 0.003193 0.003006 0.003091 0.003062 0.003062];
R1_discharge = [0.032155 0.008199 0.004763 0.004183 0.00348 0.003242 0.003193 0.003006 0.003091 0.003062 0.003062];
C1_discharge = [54.148429 21.802633 25.586141 30.914925 26.854337 32.525752 40.18035 1.503165 44.76751 43.347833 43.347833];
C1_charge = C1_discharge;

当然，你们可以参考我的方法，通过拟合方法计算出不同SOC数值下对应的阻抗系数。

2、电池Simulink模型建立

模型包括：SOC计算模块、模型参数辨识模块和端电压计算模块。

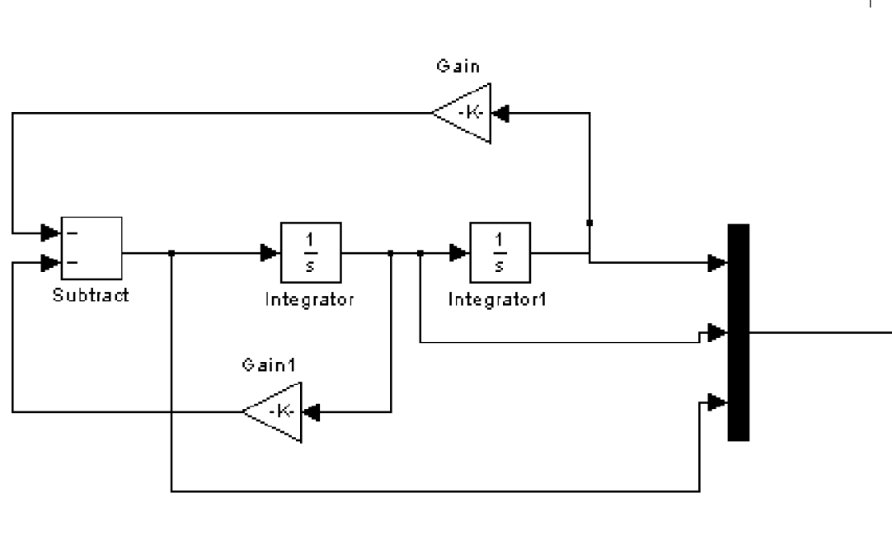
2.1、SOC计算模块

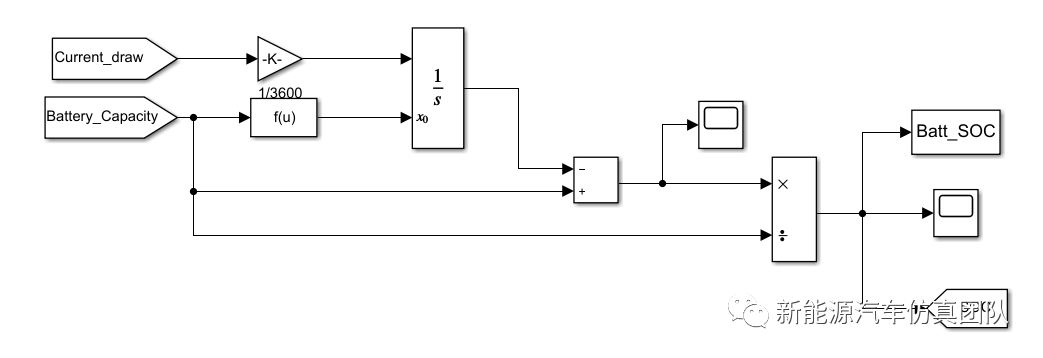
2.2、模型参数辨识模块（以R0为例）

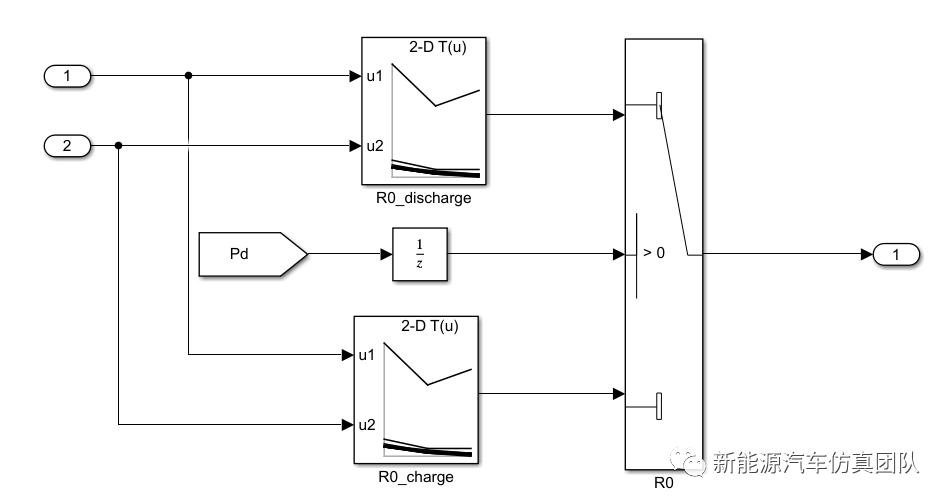
2.3、端电压计算模块

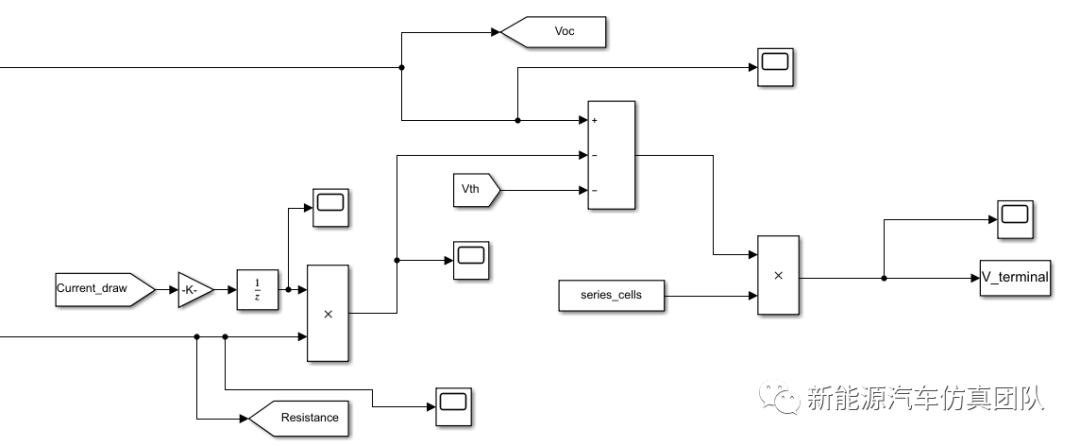
2.4、封装模块

3、试验验证

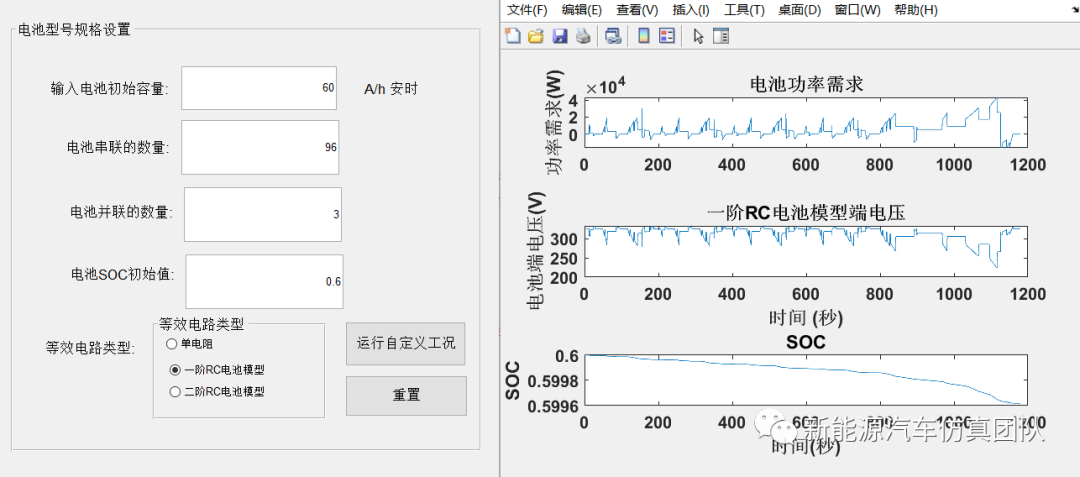
由仿真结果可知，所建立的电池模型适用于电池BMS系统开发，具有很高的精度和实时性。

结论：不管是Thevenin模型，还是二阶RC模型都能很好的反应电池的特性，适用于BMS系统。如果通过最小二乘法对电池模型辨识出现问题时，电池静置回弹电压的测试方法也是一个很好的选择！

声明：本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人，不代表德赢Vwin官网网立场。文章及其配图仅供工程师学习之用，如有内容侵权或者其他违规问题，请联系本站处理。举报投诉

锂电池

锂电池

+关注

关注
260

文章
8098

浏览量
169934
SoC系统

SoC系统

+关注

关注
0

文章
52

浏览量
10668
MATLAB仿真

MATLAB仿真

+关注

关注
4

文章
176

浏览量
19921
bms系统

bms系统

+关注

关注
0

文章
22

浏览量
10731
simulink仿真

simulink仿真

+关注

关注
0

文章
75

浏览量
8574

基于MATLAB/Simulink的系统仿真技术与应用

语言程序设计基础3，MATLAB语言在现代科学运算中的应用4，MATLAB/Simulink下数学模型建立与

发表于 06-19 13:15

参照光伏电池的物理模型，可建立用于实现其仿真的matlab...

参照光伏电池的物理模型，可建立用于实现其仿真的matlab仿真

发表于 10-26 17:24

利用MATLAB的simulink建立仿真模型

利用MATLAB的simulink建立仿真模型，与stm32cubemx搭建数据链，通过simulink

发表于 08-17 07:11

介绍一种基于matlab/simulink的异步电动机仿真模型

本文从异步电动机的数学模型着手介绍一种基于matlab/simulink的异步电动机仿真模型，使

发表于 09-06 06:42

如何去开发一种基于HAL库的模型并进行仿真呢

STM32为什么使用Matlab/Simulink呢？如何去开发一种基于HAL库的模型并进行仿真呢？

发表于 11-18 07:56

如何利用MATLAB的simulink建立仿真模型呢

如何利用MATLAB的simulink建立仿真模型呢？并与stm32cubemx搭建数据链呢？

发表于 11-18 07:17

基于MATLAB/Simulink的汽车ABS的半实物仿真系

本文所研究的是一种基于MATLAB/Simulink的汽车防抱死刹车系统（ABS）的半实物仿真的方法。本方法利用Simulink提供的

发表于 06-25 14:29 •64次下载

MIMO-OFDM的matlab和simulink仿真程序或

MIMO-OFDM的matlab和simulink仿真程序或模型(有OFDM的simulink仿真

发表于 02-08 14:38 •540次下载

一种基于Matlab的可逆变流器仿真模型

基丁逆变流器的结构和工作原理。建立一种基于Matlab的变流器的仿真结果进行对比，对所建立的仿真模型

发表于 08-12 17:30 •0次下载

基于Matlab_Simulink的QAM通信系统的仿真

利用Matlab的Simulink工具箱建立了QAM 系统的仿真模型，详细地叙述了仿真参数的设置

发表于 07-30 10:31 •98次下载

基于MATLAB/simulink的直接转矩控制离散仿真系统的研究分析

SIMUUNK是MATLAB提供用来对动态系统进行建模、仿真、分析的软件包。SIMULINK包含许多模块库，利用这些模块库可以很方便的进行复

发表于 10-17 07:57 •4831次阅读

使用MATLAB和Simulink的建模与仿真详细课件免费下载

本文档的主要内容详细介绍的是使用MATLAB和Simulink的建模与仿真详细课件免费下载包括了:1.MATLAB软件，2.简介MATLAB

发表于 11-04 17:17 •140次下载

基于MATLAB_Simulink的光伏电池建模与仿真

基于MATLAB_Simulink的光伏电池建模与仿真说明。

发表于 04-28 11:14 •104次下载

基于Matlab simulink的蓄电池双向DCDC控制模型

基于Matlab simulink的蓄电池双向DCDC控制模型(5g电源技术要求)-该资料为基于Matlab

发表于 09-28 11:02 •86次下载

一种基于MATLAB平台的直流伺服仿真模型

一种基于MATLAB平台的直流伺服仿真模型(最新开关电源技术知识)- 一种基于MATLAB平台的

发表于 09-28 12:16 •8次下载