教你怎么用负反馈控制实现纯数字锁相环-德赢Vwin官网网

首先我们做一个模块，输入信号T，代表输出时钟周期，输出时钟周期严格等于T，对于熟悉FPGA的小伙伴应该很容易。下面是小编的代码。简单的说就是建立一个状态机，对输入周期参数在产生时钟的每个周期，第一时刻更新值，然后进入下一个状态计数，计数到和输入周期一致的时候又回到初始状态。

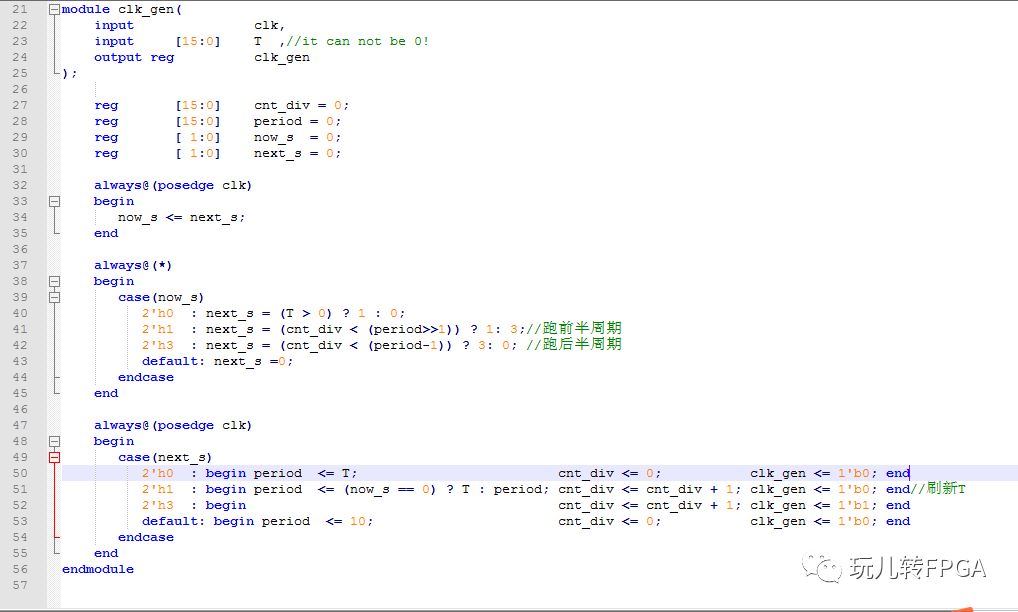
上面这个模块就是我们的控制对象，也就是说，我们要想办法让他的时钟频率Fo = 系统给定时钟频率Fi*N，也就是说: 输出时钟周期To = 系统时钟周期Ti/N。

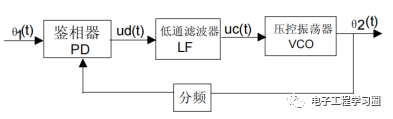
小编采用如下环路实现。从中可以看出，小编的方法反馈控制的是周期，所以一切参数都转化到周期上，输入和反馈，输出都是通过周期控制。从图中可以得出结论输出时钟周期To=N/(M*N+1)

输入时钟要求稳定，并且比系统时钟慢的越多越好，因为这样测量更准确。下面就是我们测量时钟周期的代码。反馈非常重要，因为他涉及到整个反馈环路的精度和运作效率。除以N的部分我们在另一个模块实现，因为测量时钟周期的模块是相对独立的输入和反馈都要用到，独立出来可以加强代码可重用性。这段代码就是在每个输入时钟上升沿电脑时候更新周期值。以保证周期的准确性。

控制对象和输入，反馈参数产生都已经好了，剩下的就是按照控制框图搭建反馈环路。代码如下图，代码中的Ti是在顶层产生的，输入时钟被测量后才把Ti给到环路输入。第34行是将反馈的时钟周期乘以反馈增益1/N，35行是将反馈误差乘以开环增益1/M。至此整个环路已经搭建完成！

这里附上小编顶层代码，这里从30行开始的模块就是产生上文说的Ti用的，输入时钟直接测量后，变成是种病周期T输入到feedback模块。

那么实际效果咋样呢，能工作吗？工作起来是啥样子？小编接下来就测试给大家看。测试代码如下，输出时钟周期在反馈的代码里面找，输入时钟周期是给定的，这两个找出来对比看看与理论差多远就知道了，这里M = 10,N=10。

仿真结果如下，看图1可知输出时钟周期稳定后为To = 102ns，输入时钟为Ti=1002ns，所以To/Ti = 0.1。而理论值为N/(MN+1)=10/(1010+1)=0.099。

误差err = |0.1-0.099|/0.1=1% !

我们看看下图的波形，输出时钟周期的震荡是不是很像连续系统的二阶震荡环节的阶跃响应？只不过超调不大，震荡周期比较少。这是因为我们的开环其实是一阶，加了反馈之后成了二阶系统。和控制原理书上很近似（看看离散控制部分会更觉得近似）。

声明：本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人，不代表德赢Vwin官网网立场。文章及其配图仅供工程师学习之用，如有内容侵权或者其他违规问题，请联系本站处理。举报投诉

锁相环

锁相环

+关注

关注
35

文章
584

浏览量
87734
FPGA设计

FPGA设计

+关注

关注
9

文章
428

浏览量
26505
负反馈电路

负反馈电路

+关注

关注
1

文章
35

浏览量
9272
二阶系统

二阶系统

+关注

关注
1

文章
16

浏览量
9572

FPGA实现负反馈控制纯数字锁相环

该文章是完全原创，用最简洁的语言讲清楚FPGA实现负反馈的精要。震撼！FPGA实现负反馈控制

发表于 04-30 04:50

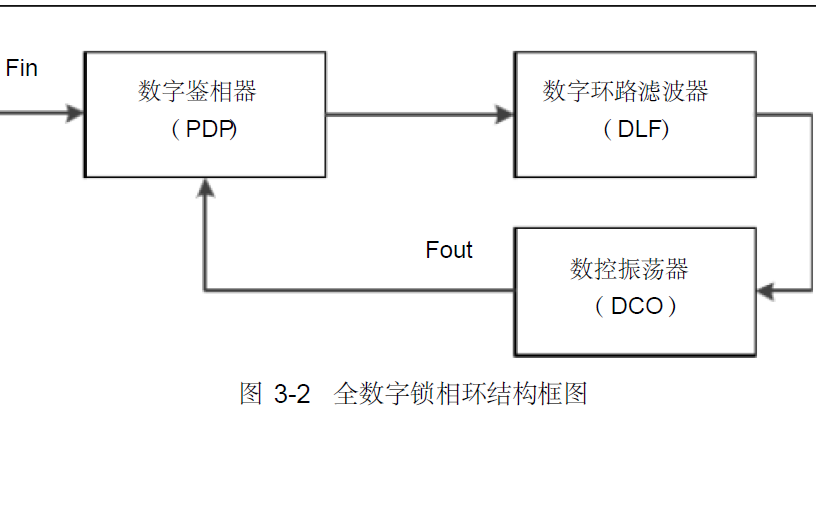
如何实现基于VHDL语言的全数字锁相环？

　随着集成电路技术的不断进步，数字化应用逐渐普及，在数字通信、电力系统自动化等方面越来越多地运用了数字锁相环。它的好处在于免去了模拟器件的繁琐，而且成本低、易

发表于 10-10 06:12

数字锁相环(DPLL),数字锁相环(DPLL)是什么?

数字锁相环(DPLL),数字锁相环(DPLL)是什么? 背景知识：随着数字电路技术的发展，数字

发表于 03-23 15:06 •5772次阅读

模拟锁相环,模拟锁相环原理解析

模拟锁相环,模拟锁相环原理解析背景知识：锁相技术是一种相位负反馈控制技术，它利用环路的反馈

发表于 03-23 15:08 •5972次阅读

锁相环

锁相环英文为PLL，即PLL锁相环。可以分为模拟锁相环和数字锁相环。两种分类的锁相环原理有较大区

发表于 10-26 12:40

基于FPGA的数字锁相环设计与实现

基于FPGA的数字锁相环设计与实现技术论文

发表于 10-30 10:38 •9次下载

用FPGA实现数字锁相环

Xilinx FPGA工程例子源码：用FPGA实现数字锁相环

发表于 06-07 15:07 •38次下载

详解FPGA数字锁相环平台

一、设计目标基于锁相环的理论，以载波恢复环为依托搭建数字锁相环平台，并在FPGA中实现锁相环的

发表于 10-16 11:36 •18次下载

基于数字锁相环消除反馈滞后的方法

一致的结果，从而消除反馈滞后一拍。所提出的锁相环仅以两个乘法器的额外开销即可大幅增强锁相环的稳定性，并且使在s域内设计的性能指标能够在z域内严格实现，克服了传统

发表于 01-02 10:30 •9次下载

使用FPGA实现数字锁相环的设计资料说明

锁相环路是一种反馈控制电路，简称锁相环（ PLL）。锁相环的特点是：利用外部输入的参考信号控制环

发表于 08-06 17:58 •26次下载

简述锁相环技术

锁相环（Phase Locked Loop，PLL）是一个闭环负反馈相位控制系统，至少包含3个基本单元电路。

发表于 04-27 15:17 •6476次阅读

锁相环设计简介

锁相环 (phase locked loop)是一种利用相位同步产生的电压，去调谐压控振荡器以产生目标频率的负反馈控制系统。

发表于 11-02 17:45 •3275次阅读

模拟锁相环和数字锁相环区别

模拟锁相环和数字锁相环的主要区别在于它们的控制方式不同。模拟锁相环是通过模拟电路来控制频率和相位

发表于 02-15 13:47 •5149次阅读

锁相环原理与公式讲解

锁相环是一种利用相位同步产生电压，去调谐压控振荡器以产生目标频率的负反馈控制系统。

发表于 06-25 09:22 •8736次阅读

锁相环的基本原理和主要作用

锁相环（Phase Locked Loop，简称PLL）是一种在电子系统中广泛应用的负反馈控制系统，其主要作用是实现输入信号与输出信号之间的相位同步。在现代通信、雷达、导航、测量等领域

发表于 05-24 16:28 •3524次阅读