相平面法
前言
非线性系统的相平面法是一种分析和研究非线性系统动力学行为的方法。相平面法通过将系统的状态变量表示为二维平面上的轨迹,来揭示非线性系统的稳定性、周期性、吸引子等特性。
对于非线性系统,其状态变量的演化不再遵循简单的线性关系。相平面法的基本思想是将非线性系统的动力学方程转化成一组一阶微分方程,并将其表示为相平面上的向量场。这样,系统的状态变量就可以在相平面上以轨迹的形式展示。
通过相平面法,可以观察到系统在相平面上的轨迹的形状和特性,从而推断系统的稳定性和行为。常见的特性包括平衡点(稳定点)、极限环、吸引子等。通过分析轨迹的形状、轨迹的相交点以及轨迹的变化趋势,可以确定系统的稳定性、周期性或者混沌行为。
相平面法也存在一些缺点需要考虑:
- 限于二维系统:相平面法只适用于二维系统,对于高维系统无法直接应用。在高维系统中,相平面法无法提供完整的动力学行为描述,因为它无法展示高维空间中的复杂轨迹。
- 无法精确解析求解:相平面法主要是基于图形观察和分析,而不是通过解析计算得到精确解。因此,特别是对于非线性系统和复杂的微分方程,相平面法无法提供准确的定量信息。
- 可视化有限:相平面法能够提供关于系统行为的直观图像,但在大规模系统或长时间尺度上,图像可能变得复杂且难以解释。对于复杂的相轨迹和相平面,仅凭人眼可能无法完全捕捉到细微的变化和行为特征。
- 不能涵盖所有情况:相平面法主要用于研究振荡、稳定性和周期性等特定系统行为。对于其他类型的非线性动力学行为,如混沌行为,相平面法可能无法提供全面的理解。
- 对数值求解的依赖:在实际应用中,相平面法通常依赖于数值计算和数值vwin 。这涉及到选择适当的数值方法,并且对数值误差和数值稳定性要有充分的认识。
相平面


奇点
平衡点是使系统永久停驻的点,即


非线性系统的相平面分析
在奇点附近,相轨迹的特征与线性系统比较接近,因此可以通过进行非线性系统的线性化,然后进行分析。常用的方法是利用泰勒公式进行展开。泰勒公式是一个关于函数在某点附近的展开式,通过展开可以将非线性函数近似为线性函数,从而方便进行局部分析。

极限环
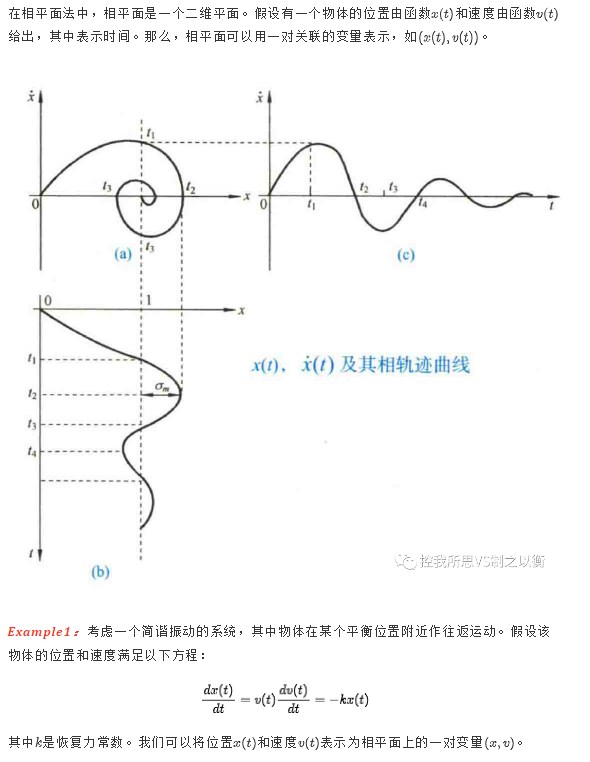
奇线是相轨迹中的特殊情况,将相平面划分为具有不同运动特性的区域。最常见的奇线是极限环。非线性系统会出现自振荡,因此在相平面上会形成一条孤立的曲线,这条曲线附近的相轨迹会逐渐趋向或离开这条曲线,这就是极限环。
极限环将相平面分为内部平面和外部平面两部分,轨迹无法从极限环内部穿过进入外部,反之亦然。这样就将相平面划分为具有不同运动特性的区域,因此,极限环也是相平面上的分界线,对于确定系统的全部运动状态非常重要。
需要指出的是,并非相平面上的所有孤立曲线都是极限环。在无阻尼的线性二阶系统中,由于没有阻尼造成的能量损耗,相平面图是一系列连续的闭合曲线,这些曲线并非极限环,因为它们不是孤立的,在任何特定闭合曲线的邻近仍然存在其他的曲线。而极限环是相互孤立的,在任何极限环的邻近不可能有其他的极限环。极限环是非线性系统中独有的现象,它仅在非保守系统中出现。这种周期运动的原因不在于系统无阻尼,而是系统的非线性特性,导致系统能量交替变化,因此可以从非周期性的能源中获取能量,从而维持周期运动。
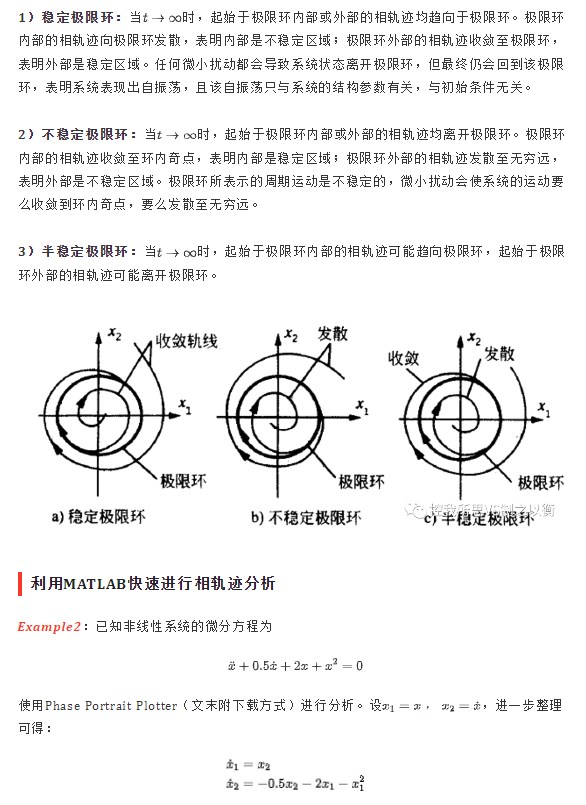
根据极限环附近相轨迹的运动特点,极限环可分为以下三种类型:
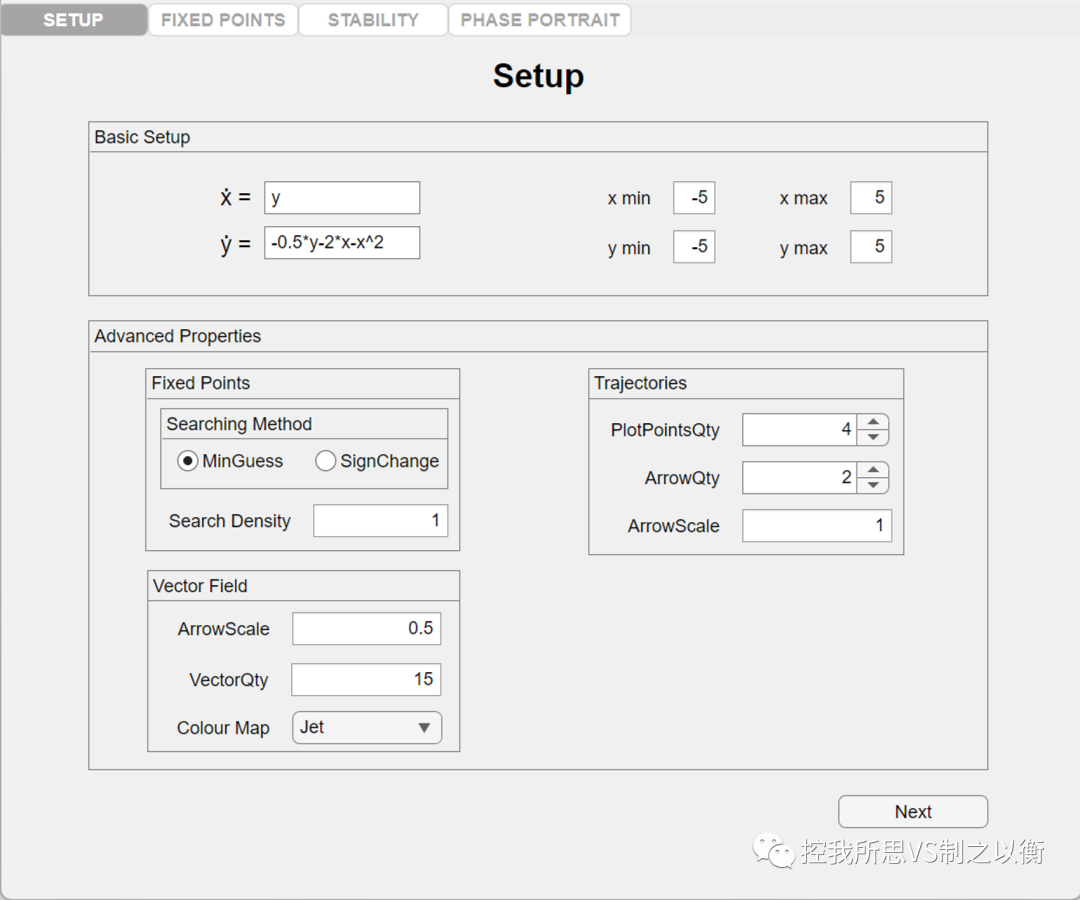
得出平衡点(奇点)

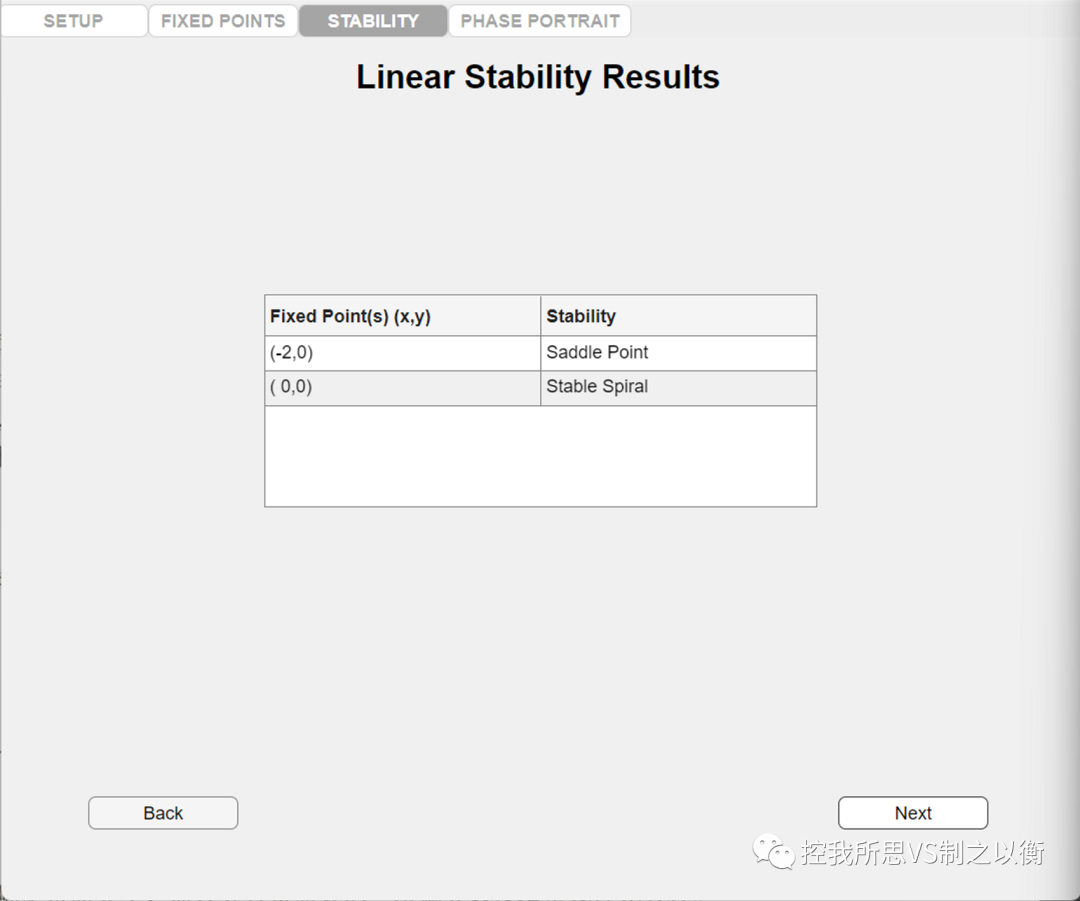
得到奇点类型
绘制相轨迹
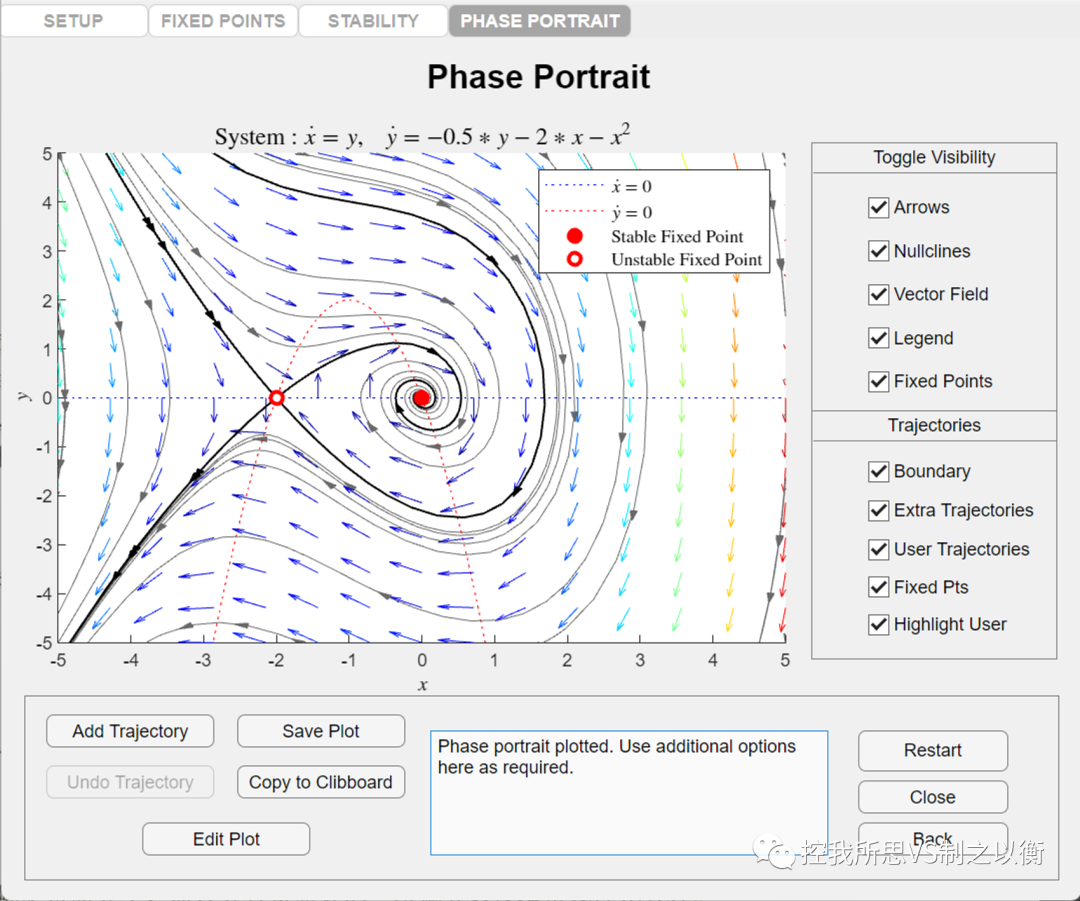
根据奇点的位置和类型,图中与鞍点(-2,0)相交的两条相轨迹可称为奇线,将相平面划分为两个区域:系统的稳定区域位于相平面图中的内区域,而不稳定区域位于外区域。当初始条件位于阴影线内区域时,系统的运动将收敛至原点;当初始条件位于阴影线外区域时,系统的运动将发散至无穷大。该例说明非线性系统的运动及其稳定性与初始条件有关。
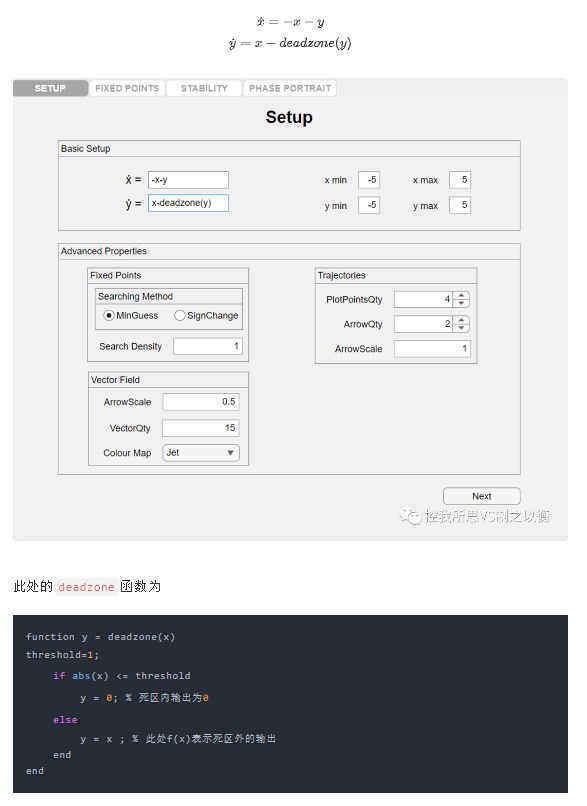
Example3 :已知带死区特性的非线性系统的微分方程为
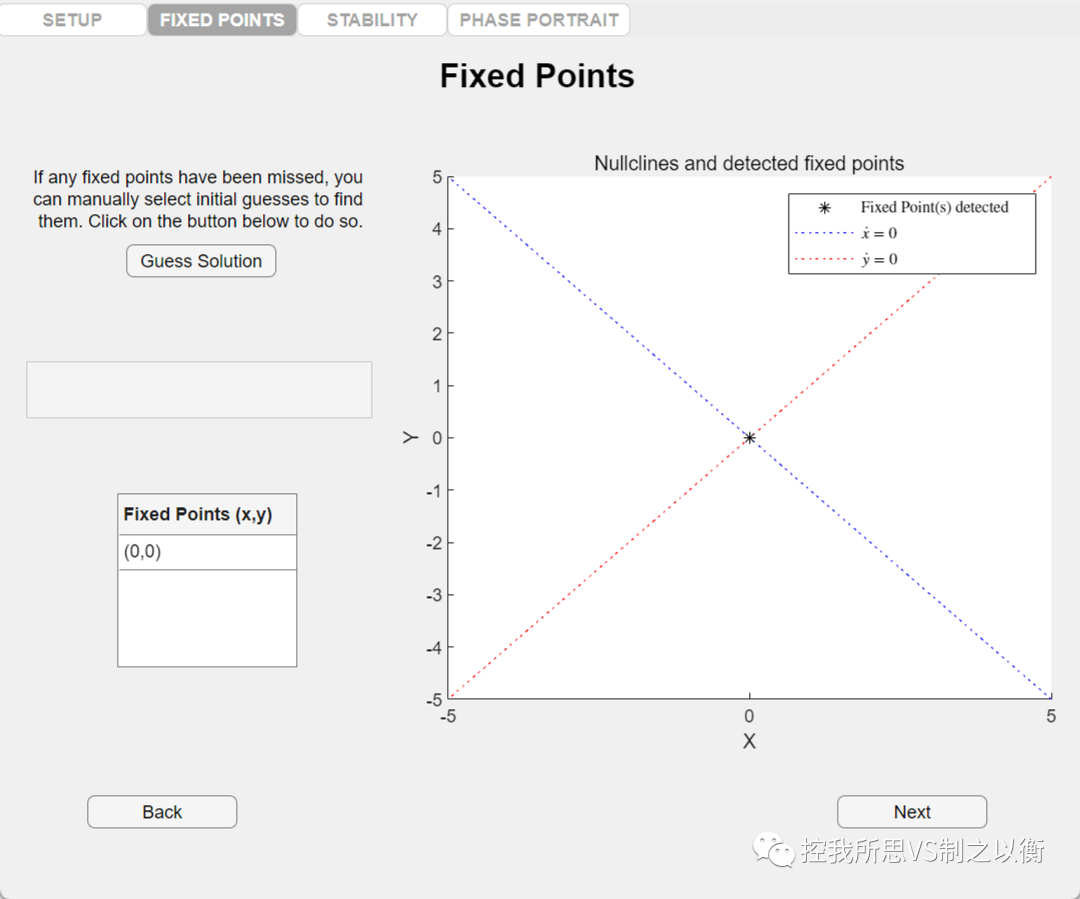
确定平衡点
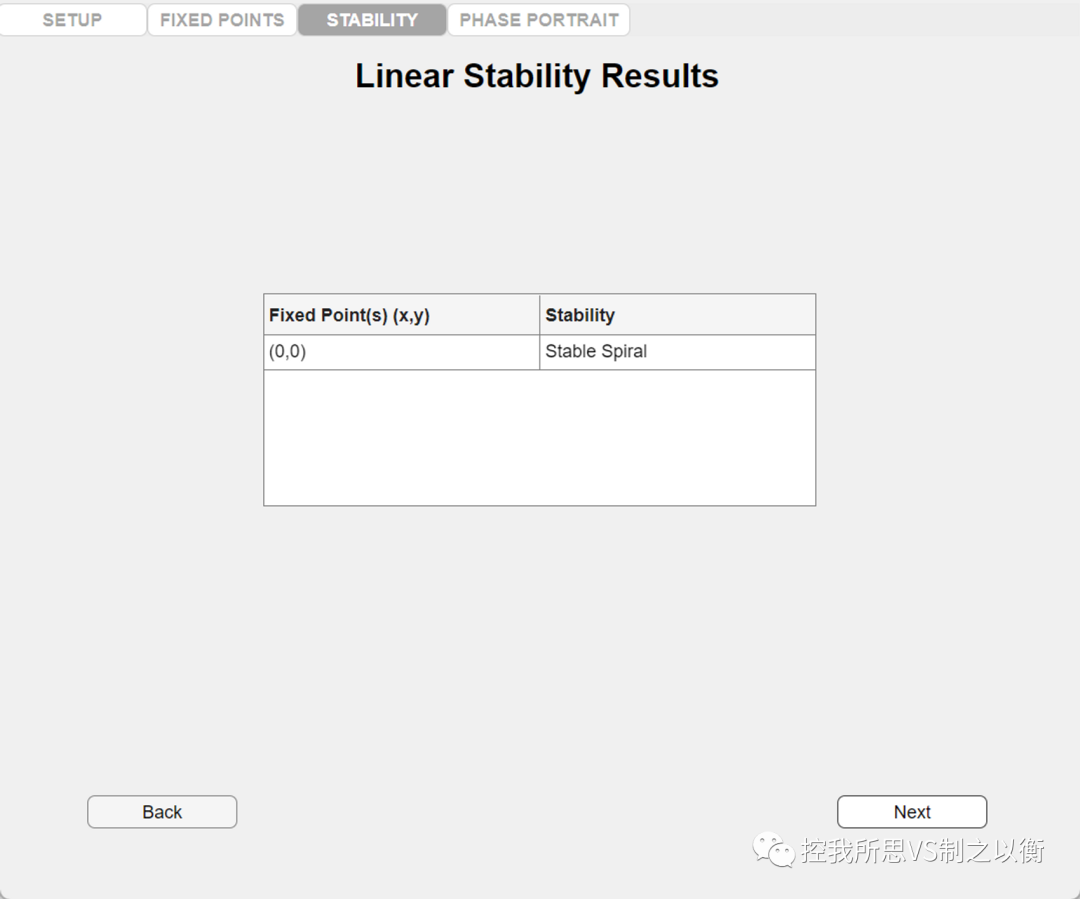
得到奇点类型
得到相轨迹

-
状态机
+关注
关注
2文章
492浏览量
27526 -
MATLAB仿真
+关注
关注
4文章
176浏览量
19921 -
非线性系统
+关注
关注
0文章
20浏览量
7879 -
二阶系统
+关注
关注
1文章
16浏览量
9572
发布评论请先 登录
相关推荐
基于多模型的非线性系统广义预测控制
基于正交小波网络的非线性系统辨识
非线性系统输出反馈控制
一种典型的非线性系统分析
非线性系统辨识
非线性系统辨识模糊模型参数收敛问题研究
自动控制系统教程之非线性系统分析的资料免费下载
何长安非线性系统控制理论的PDF电子书免费下载




 浅析非线性系统的相平面法
浅析非线性系统的相平面法











评论