在这一节中,我们来学习如何使用程序来实现一棵文件树。在上一节中,我们了解到使用文件树的方式来整合计算机中所有的资源,而这一棵文件树则是一棵多叉树。也就是说,树上的每一个节点都可能有多个子节点。
而这样的一棵多叉树在计算机中来实现是较为复杂的,使用起来也不方便。例如我们想要为节点1增加一个子节点2,之后再为节点1增加一个子节点3,之后再为节点1增加一个子节点4。整个过程如下图:
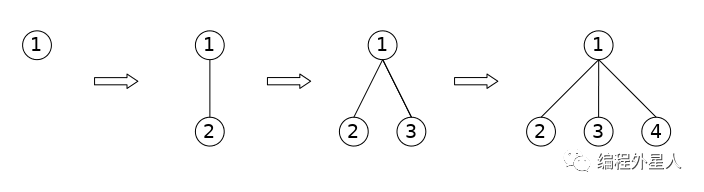
由于这是一棵多叉树,因此节点1可能具有多个子节点。这样一来,在为节点1分配内存时,我们就无法确定的为其分配指定大小,由于树型结构的特点,我们需要使用一个指针变量用于指向其一个子节点,而如果其具有2个子节点,则需要2个指针变量,如果其具有3个子节点,则需要3个指针变量。
于是对于多叉树来说,当一个节点增加一个子节点时,当前节点也需要发生变化,也就是需要重新申请一个较大的内存空间用于存放更多的指针变量。同样的,当一个节点的子节点被删除时,也需要重新申请内存,释放多余的指针变量。这对于编程实现多叉树来说,是很复杂的,也是低效的。因此我们有必要寻找一种简洁的办法来处理多叉树的实现问题。
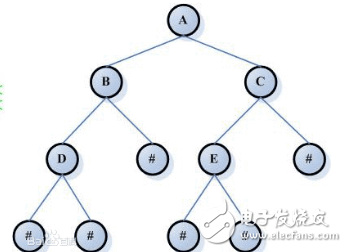
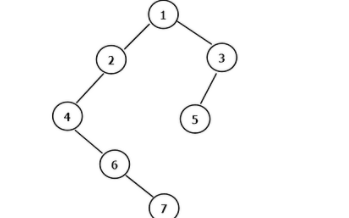
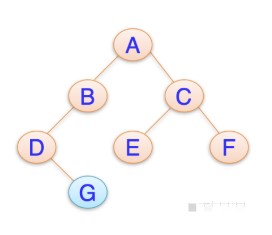
我们知道,使用计算机编程来实现一个二叉树是非常简单的,每一个节点除了实际数据区域外只需要额外两个指针用于存放其左孩子节点和右孩子节点即可,而且其内存申请和释放都很简洁。二叉树就是每一个节点的子节点最多不能超过2个节点,如下图则是一个二叉树:

为了解决多叉树的问题,我们自然想到是否能将一个多叉树转化为一个二叉树,并使用计算机程序来实现呢?答案是肯定的!其实,每一棵多叉树都可以转化为一个等价的二叉树。进而可以将一个具有多个多叉树的森林转化为一个与之等价的二叉树。
具体转化的过程是这样的:我们可以定义一个二叉树的节点,并定义两个指针变量,这两个指针变量分别为指向其“子节点”(child)和其“兄弟节点”(sibling),也就是说,一个二叉树的两个叉,左侧表示其孩子,而右侧表示其兄弟。于是我们就可以将一个多叉树转化一个二叉树,具体转化过程如下:

上图中的多叉树和二叉树是等价的,这两棵树所表示的内容完全一致,只是在结构上不同而已。也就是说这棵多叉树可以转化为二叉树,二叉树也可以转化为多叉树,本质上讲它们二者是可以相互转化的,而没有任何的不同。
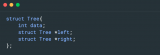
对于这棵二叉树来讲,其“左叉”表示其孩子节点,而“右叉”表示其兄弟节点。而二叉树在计算机程序中是比较容易实现的。接下来我们就定义这样一棵二叉树,用于表示其原有的多叉树:
typedef struct vfs_node_s
{
struct vfs_node_s *child;
struct vfs_node_s *sibling;
char name[200];
} vfs_node_s;
我们简单的定义name属性为表示这个节点的数据内容,而左叉child为其子节点,而右叉sibling为其兄弟节点。然后实现两函数用于初始化和销毁这个虚拟文件树:
int vfs_init(void)
{
vfs = malloc(sizeof(vfs_s));
vfs- >root = malloc(sizeof(vfs_node_s));
strncpy(vfs- >root- >name, "/", NODE_NAME_SIZE);
vfs- >root- >child = NULL;
vfs- >root- >sibling = NULL;
return 0;
}
int vfs_destory(void)
{
vfs_destory_r(&vfs- >root);
free(vfs);
return 0;
}
完成初始化和销毁虚拟文件树之后我们再来实现对任意节点进行的插入和删除操作,也就是说针对虚拟文件树,我们在指定位置插入一个新的节点:
int vfs_insert_node(char *path, file_operations_s ops)
{
if (path[0] != '/')
{
return -1;
}
//插入子节点,调用递归函数
int ret = vfs_insert_node_r(&vfs- >root- >child, &path[1], ops);
return ret;
}
int vfs_insert_node_r(vfs_node_s **node, char *abs_path, file_operations_s ops)
{
if (node == NULL)
{
return -1;
}
if (abs_path == NULL)
{
return -1;
}
if (abs_path[0] == 0)
{
return -1;
}
char node_name[NODE_NAME_SIZE] = {0};
//找到虚拟文件树上的指定路径
char *p = abs_path;
for (int i = 0; *p != '/' && *p != 0 && i < NODE_NAME_SIZE; i++)
{
node_name[i] = *p++;
}
if (*p == '/' && *p != 0)
{
p++;
}
//查找其所有兄弟节点
while (*node != NULL)
{
//找到兄弟节点
if (strcmp((*node)- >name, node_name) == 0)
{
//递归执行其子节点插入操作
return vfs_insert_node_r(&(*node)- >child, p, ops);
}
node = &(*node)- >sibling;
}
//最后生成一个新节点
vfs_node_s *node_new = malloc(sizeof(vfs_node_s));
strncpy(node_new- >name, node_name, NODE_NAME_SIZE);
node_new- >child = NULL;
node_new- >sibling = NULL;
*node = node_new;
//将新节点插入
if (*p != 0)
{
return vfs_insert_node_r(&node_new- >child, p, ops);
}
return 0;
}
这样,我们就完成了二叉树的创建、销毁与插入功能,当然还应该实现针对指定节点的删除功能,这里我们不再给出具体实现代码,请读者自行完成。这样的二叉树就可以完整的表示我们计算机中的虚拟文件系统(根节点是虚拟节点,并非是实际存在的,Linux系统中的根节点是实际的硬盘分区,因此Linux的文件系统不是虚拟文件系统)。
此后我们就可以用这一棵二叉树来表示计算机中的所有资源了,具体方式则是将资源抽象成一个文件,挂载到文件系统中,成为文件系统中的一个节点,这样就可以方便用户管理和使用这些资源了。
-
计算机
+关注
关注
19文章
7488浏览量
87846 -
Linux系统
+关注
关注
4文章
593浏览量
27392 -
二叉树
+关注
关注
0文章
74浏览量
12324
发布评论请先 登录
相关推荐
基于二叉树的时序电路测试序列设计
二叉树层次遍历算法的验证
红黑树(Red Black Tree)是一种自平衡的二叉搜索树
二叉树操作的相关知识和代码详解
二叉树的前序遍历非递归实现
二叉排序树AVL如何实现动态平衡




 文件系统-多叉树与二叉树的转化
文件系统-多叉树与二叉树的转化










评论