虚零点法
虚零点法是指引入的对应零点只出现在环路增益A(s)F(s)中,而不出现在闭环传递函数H(S)中,能够实现此目的的零点,只能是在反馈环路F(S)中引入的零点,现假设反馈环路F(s)=F1(s)(n1+s),F(S)中存在一个零点n1,则:

在反馈通道中引入的零点就是虚零点,原则上可以在反馈网络的以下三个位置引入虚零点:
- 反馈网络中间
- 反馈网络的输入端,即放大器的输出端
- 反馈网络的输出端,即放大器的输入端
- 虚零点对根轨迹的影响
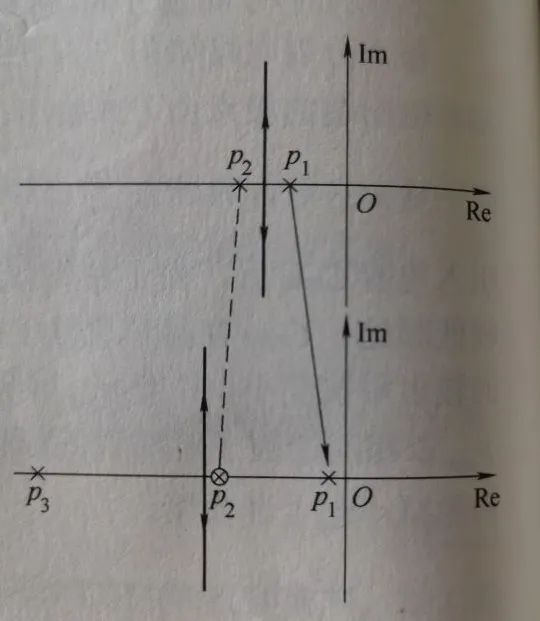
虚零点应该如何放置才可以获得期望的频率补偿?下面以常见的二阶系统为例,假设其环路增益有两个极点p1、p2和一个零点n1,则其根轨迹特征方程式可以表示为:

我们费了半天劲推导以上公式,目的是什么?可能很多读者有点迷惑,在此郑重声明如下:费了半天劲推导以上公式,不是为了保卫宇宙和平,我们推导的目的,就是要根据要求的频率补偿而计算所需要的补偿零点位置!
比如,现在我们想把一个低通特性的系统的频率特性补偿为巴特沃斯特性,我们知道巴特沃斯低通的原型分母可以写为:

2.虚零点在放大器的输入端实现
虚零点在输入端实现时,使用什么类型器件主要取决于源阻抗的类型(是电阻、还是电容、电感)以及使用何种反馈网络,如下图:
下面两图的Zp为虚零点补偿元件,Zs为源阻抗,两图分别在放大器输入端补偿,而等效在反馈网络的输出端引入虚零点:
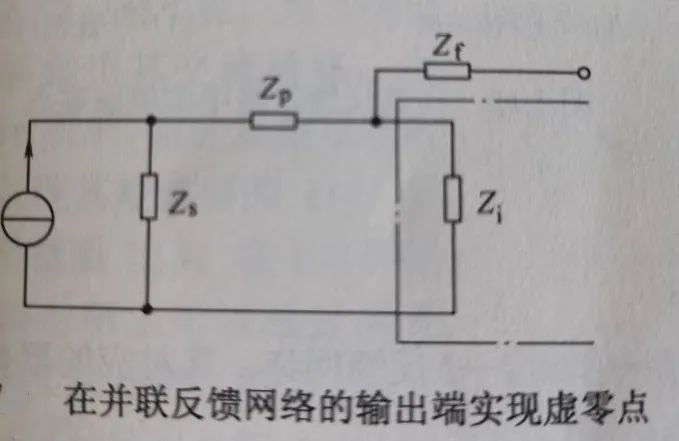
对于输入并联负反馈,补偿元件Zp的选择如下:
1)若Zs为电阻,则Zp为电感
则补偿后的阻抗由Zs=Rs,变为Rs+s*L,引入一个左半平面的零点;而且低频时Zp可以忽略,传递特性保持补偿前的状态,这正是前述公式推导的基本假设要求,也是我们在第一篇频率补偿推文中提到的:频率补偿不是完全推翻原特性,而是局部修改频率特性,它不应该改变整体趋势;如要改变整体频率特性,那就不叫频率补偿了,那是重新设计。
复杂的vwin 电路设计,涉及方方面面的指标,各种指标间相互牵扯,就是著名的八边形法则,见模拟集成电路大神”拉扎微”的书的第43页,如下:

各种指标设计相互掣肘,我们该如何下手?一般可以按照噪声=>失真=>频率补偿...等顺序来做,具体缘由以后推文再说,可见频率补偿并不是推翻了重新设计,而是在噪声、失真原设计结构的基础上,微调频率特性,调整太大,前期噪声、失真阶段的设计成果就完全作废了。
2)若Zs为电容,则Zp为电阻和(或)电感
则补偿后的阻抗由Zs=1/sc,变为1/sc+sL或1/sc+R或1/sc+sL+R,引入一个左半平面的零点
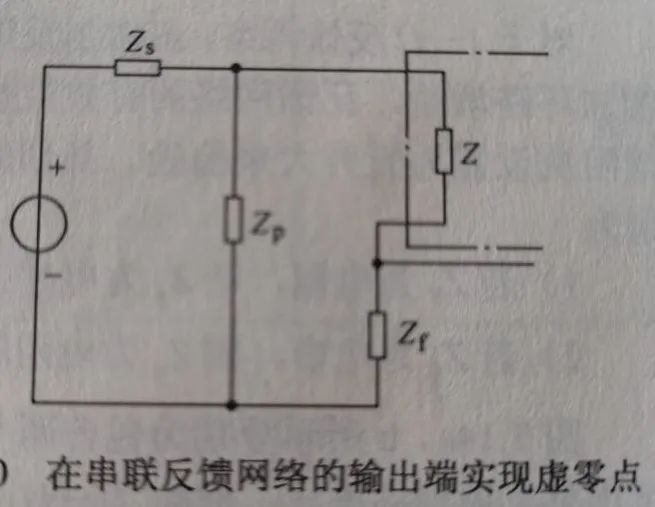
1)若Zs为电阻,则Zp为电容
2)若Zs为电感,则Zp为电阻和(或)电容
在放大器输入端实现虚零点,应该注意补偿器件对噪声的影响,由于补偿电阻的噪声直接加在放大器输入端,可能破坏前期的噪声设计指标。所以前期噪声设计应该留有余量。
3.虚零点在放大器的输出端实现
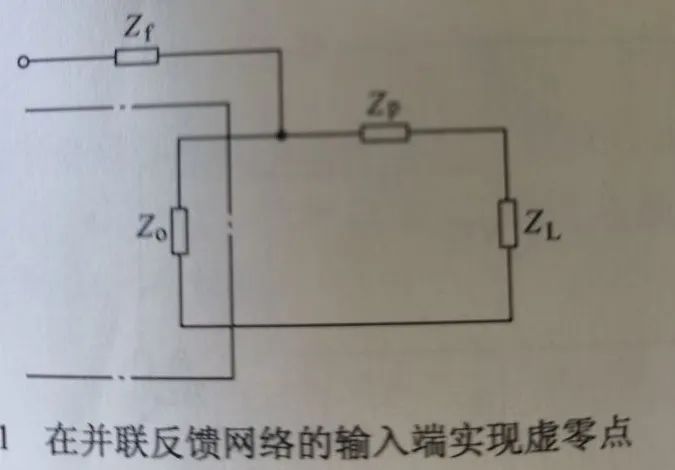
上图为输出电压负反馈,Zp为零点补偿元件:
1)若负载ZL为电阻,则Zp可为电感
2)若负载ZL为电容,则Zp为电阻和(或)电感
下图为输出电流负反馈:
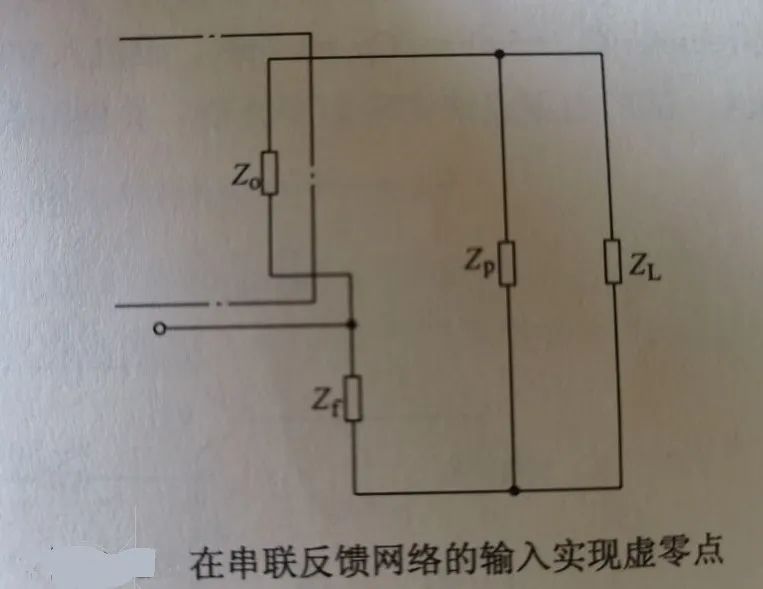
上图为输出电流负反馈,Zp为零点补偿元件:
1)若负载ZL为电阻,则Zp可为电容
2)若负载ZL为电感,则Zp为电阻和(或)电容
4.虚零点在放大器的反馈网络中的实现
与放大器输入或输出实现虚零点不同,在反馈网络中的虚零点不仅影响系统噪声,还会影响系统的失真特性,如下:

对于U-I型补偿结构:
- 若Zf为电阻,则补偿元件Zp为电容
- 若Zf为电感,则补偿元件Zp为电阻和(或)电容
对于I-U型补偿结构:
- 若Zf为电阻,则补偿元件Zp为电感
- 若Zf为电容,则补偿元件Zp为电阻和(或)电感
补偿也可采用U-U结构或I-I结构,而U-U结构可以开成由U-I、I-U构成的双反馈网络,反馈元件类型选择同单反馈结构:

5.设计应用举例

上图是晶体管构成的两级电压串联负反馈电路,其放大倍数通过估算,一看就知道基本上为10倍,假设晶体管的

如前所述,下图把可能的频率补偿位置与补偿元件都列举出来,实际补偿往往只选一个位置:
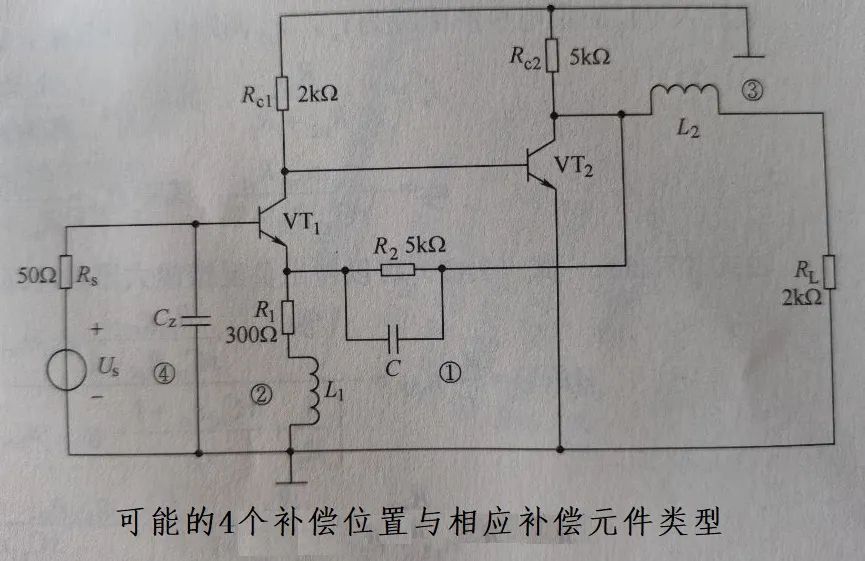
上图①、②为反馈网络中的双补偿,
③为反馈网络输入端的虚零点补偿,
4为反馈网络输入端的虚零点补偿。具体看查看前述推文。
选定①补偿方式,则其环路增益计算如下:

注意断点的位置,环路增益计算是从断点位置右侧沿环路一周,计算到断点左侧,断点可以是环路中的任意位置,原则就是要方便计算:
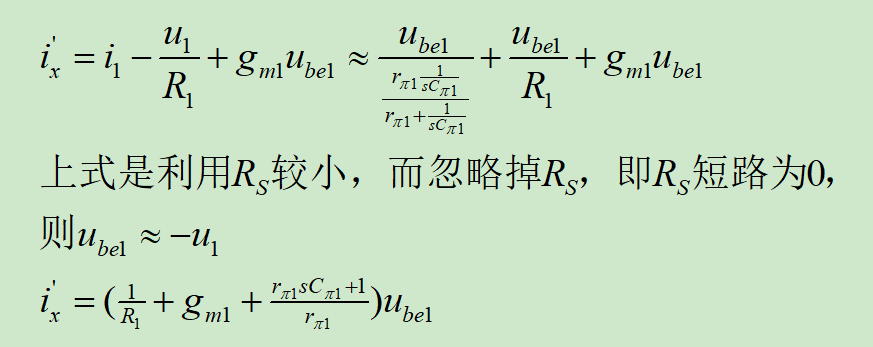
由于R2>>R1,则

-
放大器
+关注
关注
143文章
13583浏览量
213364 -
电阻器
+关注
关注
21文章
3779浏览量
62112 -
CMOS集成电路
+关注
关注
4文章
41浏览量
14250 -
二阶系统
+关注
关注
1文章
16浏览量
9572 -
负载电容
+关注
关注
0文章
138浏览量
10438
发布评论请先 登录
相关推荐




 模拟CMOS集成电路设计:虚零点法
模拟CMOS集成电路设计:虚零点法











评论