典型数字调制信号的矢量图描述
在vwin 调制中，载波参量的改变是按连续的模拟信息。在数字调制中，这些载波参数(幅度，频率和相位)的变化由离散的数字信号决定。从这个意义上讲，数字调制和模拟调制并无本质区别。数字调制信号只须表示离散的调制状态，这些离散状态在矢量图上称为符号点 (symbol point)，符号点的组合称为星座图(constellation)。
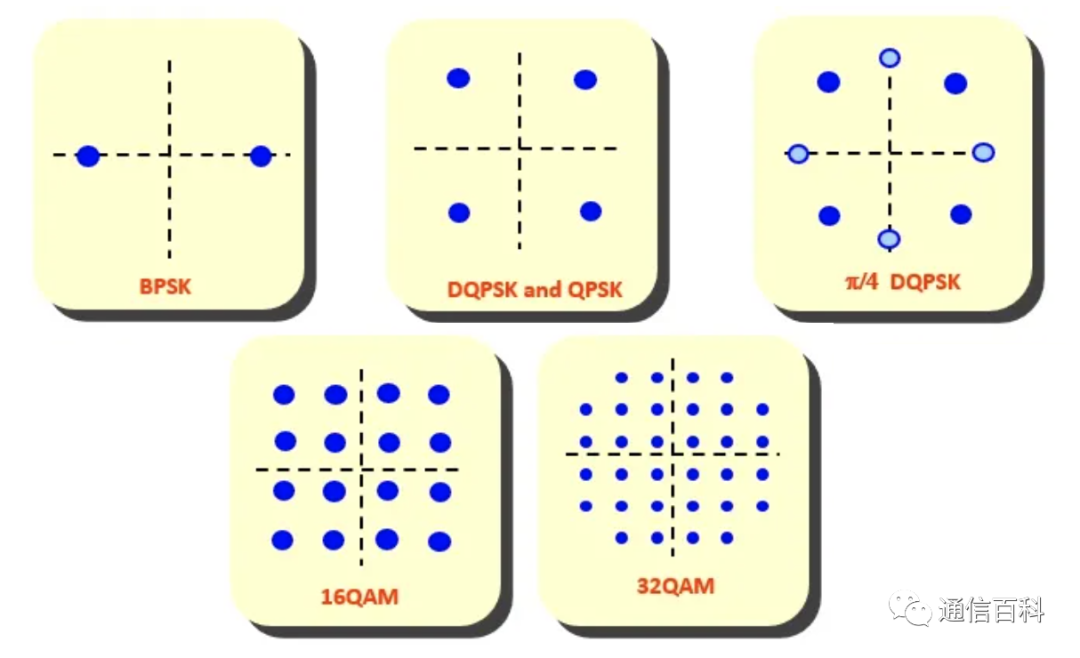
以上图中的 16 QAM 格式为例，每个符号表示着四个二进制位的一种可能组合。对于这四个二进制位来说，总共可能有16个组合。换言之，每个符号表示着四位。为了提高数据带宽，我们可以增加每个符号表示的位数，这样可以提高频谱效率。
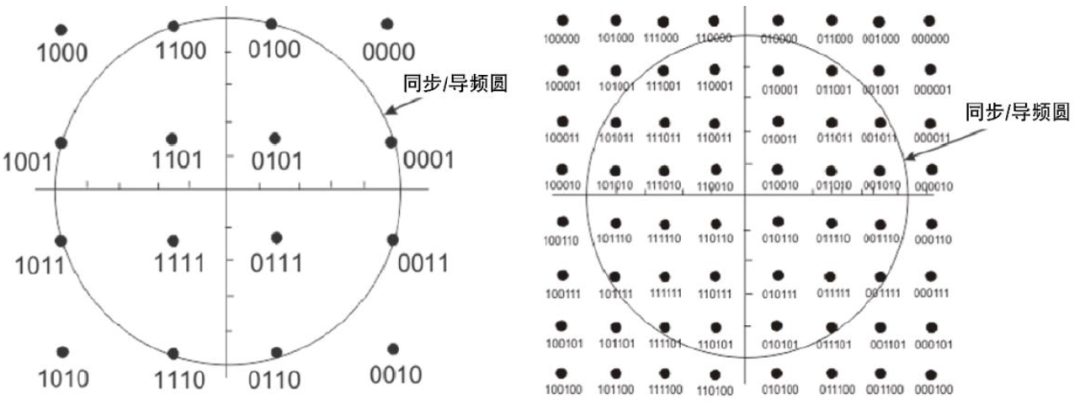
不过，随着星座图中符号数量的增加，符号间的距离开始变小。符号越来越接近，因此就越容易受到噪声和失真的影响，出现错误。因此，星座图和符号星座图展示了 调制格式的可用符号。从下图可以看出，当从 16-QAM 格式变为 64-QAM 格式时，符号密度的增加。
数字调制概念
我们先来了解一些关键的术语。
比特 Bit ：是通信系统传输信息的单位，一般指通信系统中传输的有用信息。
比特率 Bit Rate ：是比特的传输速率，也就是通信系统时间内的信息传输速率，单位是比特/秒(bit/s)。
符号 Symbol ：是信息调制载波的离散状态，也就是矢量，是与载波和调制方式紧密联系在一起的概念。模拟调制也可以说有符号，只是符号数量无穷多，无法直接分析和观察。因此只在数字调制中讨论符号，其符号数目是有限个。符号并不是信息，但信息是通过数字调制映射为载波状态即符号来传输的。
码元速率或符号率 Symbol Rate ：载波调制符号的转换速率，实际上是载波状态的变化速率。符号率越高，相应信息传输速率也越高，但信号中包含的频谱成分也越高，占用频带越宽。单位是波特 (Baud)。
星座图 Constellation：调制信号在IQ平面上的所有符号点的组合。星座图定义调制技术的信号分布与调制数字比特之间的映射关系。一种调制技术的特性可由信号分布和映射完全定义，即可由星座图来完全定义。
矢量图 Vector Diagram：调制信号在符号点间变化的过程描述。矢量图不仅显示星座点，而且显示星座点之间的转换过程。
眼图 Eye Diagram：检查数字信号传输畸变的一种形象直观方法。它是解调后在低通滤波器输出未经再生的基带信号，在示波器上用位定时作为外同步时重复扫描显示的波形。
比特率与符号率(波特率)的关系
比特率是系统传输比特流的频率。符号率等于比特率除以每个符号可以传输的比特数。例如，在 QPSK 中，每个符号表示两个比特。QPSK 的符号率就是其比特率的一半。信号带宽和符号率成正比。
符号率=比特率/每个符号传输的比特数我们讨论的调制信号都可以用正弦函数来表示(什么是调制?)：
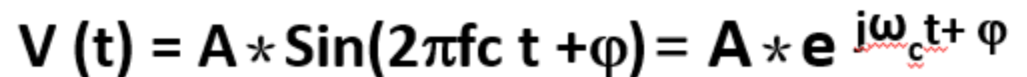
其中，A代表信号幅度，也是我们常说的信号电平。可以用不同的量度表征它，如功率，电压等。Sin括号内的是信号的瞬时相位，它分为两项：
第一项是由载波频率fc决定的相位，是单位时间相位的变化;
第二项是相对于零度的起始相位j 。所以频率实际是瞬时相位表达式的一部分，是相位变化的速度。
有两种不同于前面的矢量图表示方法：极坐标图和 I/Q直角坐标图。这两种表示方法都十分常用，如何理解 I/Q 信号, 星座图及相关变量?
极坐标图表示的矢量的参数是幅度和瞬时相位，一般表示为AÐq。
因为所有调制形式针对载波的改变都是幅度、相位以及可以由相位推导的频率。极坐标图是分析调制技术矢量参数的主要描述方式。
I/Q直角坐标图表示矢量的参数不是直接的幅度和瞬时相位，而是把它们投影在I/Q直角坐标轴上，采用 I 轴和Q轴的投影分量来确定矢量
使用 I/Q直角坐标图是因为和 I/Q调制的表示方法完全一样
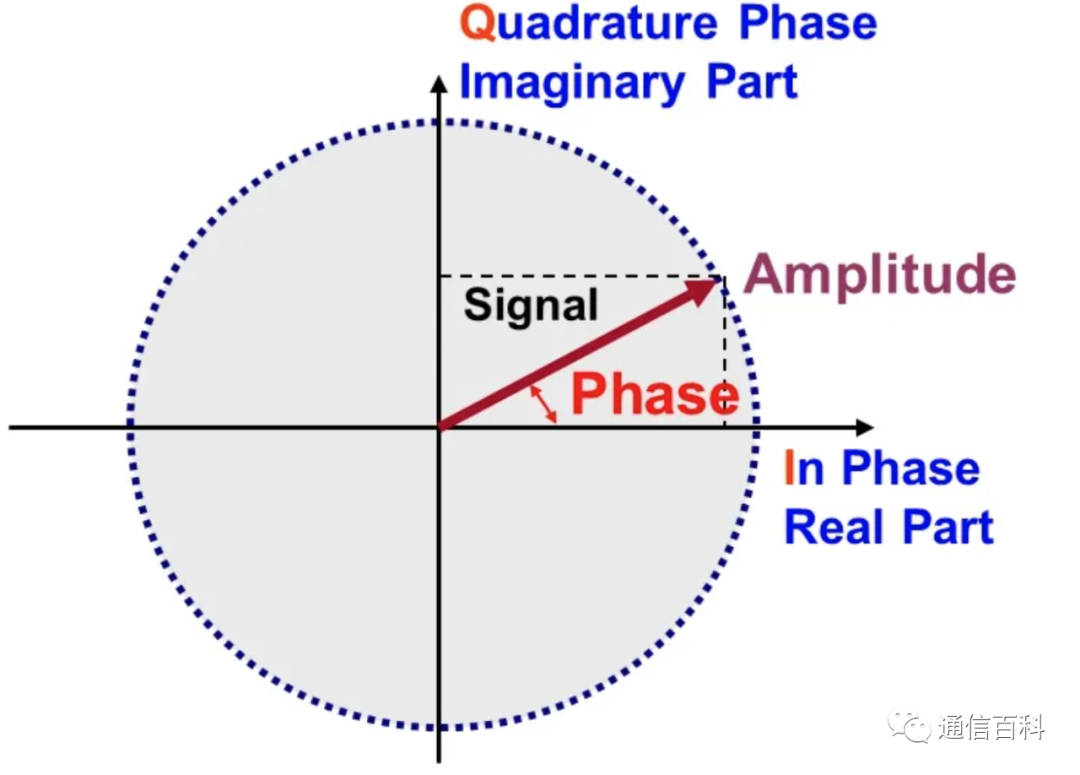
矢量的表示方法
用矢量来描述一个正弦波是非常方便的。在极坐标中，矢量表示正弦波的峰值电压幅度对于相位改变量的关系。相位旋转360度表示一个完整的频率周期。请注意，相向的符号提供了一种表示正弦波相位随时间变化的便捷方法。
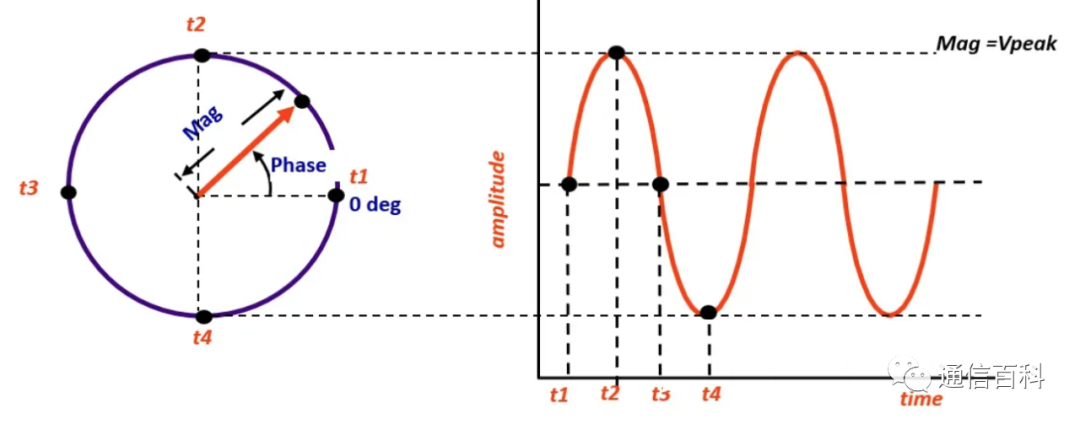
其中，幅度：是一个绝对值 相位：相对于一个参考值(载波)。
幅度：是一个绝对值
相位：相对于一个参考值(载波)
上图中正弦波表示了一种信号幅度随时间变化的过程。矢量不能直接提供任何频率信息。事实上，我们测量矢量相对于载波信号的参考相位。这意味着，矢量仅在频率不同时会发生旋转。
任何极坐标图中，如图1沿径向的变化意味着信号幅度改变，如图2角度的变化意味着信号相位改变(且仅仅是相位发生变化)。在极坐标中，可以观察各种信号：AM调制，PM调制，FM调制。记住，幅度和相位变化都是相对于未调制载波的。
传统的时域和频域可以直观的观察调制信号，但无法对调制参数进行深入的分析和测量，所以引入了矢量描述方法。
典型调制信号的矢量图描述
矢量图 (Vector diagram) 是描述矢量信号变化轨迹的一种直观方式：
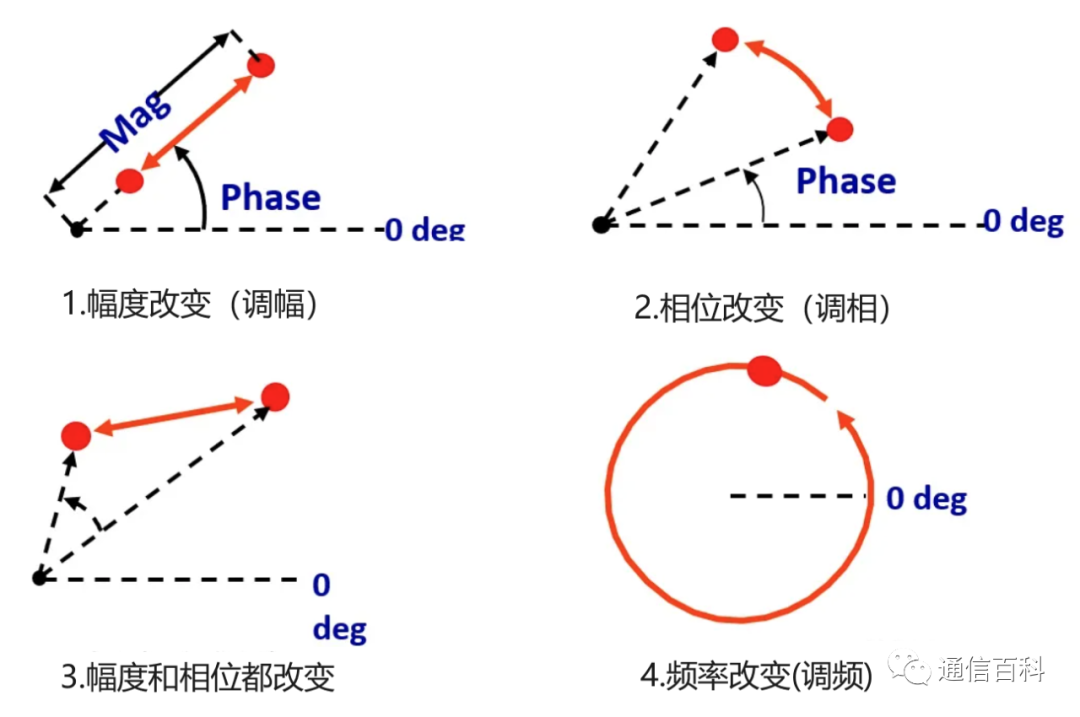
图1实例是调幅(AM)波。因为调幅波的频率是不变的，射频频率与载频之间是固定不变的，仅相差一个初相角。看起来是一条从原点到某最大点之间的直线。其信号幅度则在两个圆点之间变化，其变化值与单位园半径之比就是信号的调幅指数。
图2实例是调角波，包括调频波(FM)或调相波(PM)。因为调角波的信号幅度是固定不变的，仅在圆周上某个初相角处产生角度的变化。看起来就是在圆周上某一段弧线上变化。
图3表示一个调幅信号的相位也不是绝对不变的，常伴随着小量不希望的相位变化，称为寄生调频或剩余调频(或调相)。一个调角信号的幅度也不是完全恒定的，因为调角信号中存在寄生调幅。结果在极坐标图中的信号轨迹如图三角形所示，它同时存在幅度与相位变化。
调幅或角系统产生的这种寄生调制，会使调制信号产生失真。调幅信号直线轨迹变成了折线或曲线。若在系统传递函数中存在滞后现象，则直线也可能变为环线状。总之，这些失真会导致解调信号的参数变化。
调幅或角系统产生的这种寄生调制，会使调制信号产生失真;
如果频率不是一个恒定值，则转速也会变化。
审核编辑：汤梓红
-
通信系统
+关注
关注
6文章
1187浏览量
53322 -
数字调制
+关注
关注
0文章
46浏览量
13007 -
波特率
+关注
关注
2文章
307浏览量
34115 -
比特率
+关注
关注
1文章
28浏览量
10609 -
矢量图
+关注
关注
2文章
15浏览量
7422
原文标题：一文搞懂 "星座图" 原理！
文章出处：【微信号：5G通信，微信公众号：5G通信】欢迎添加关注！文章转载请注明出处。
发布评论请先 登录
相关推荐
如何生成和分析毫米波范围内的宽带数字调制信号
AN描述如何测量数字调制载波
基于FPGA和DDS的数字调制信号发生器设计
信号发生器TSG4100A实现多功能矢量和数字调制
利用矢量信号分析仪如何对IQ调制器中EVM性能进行优化
解析VSA的矢量调制分析和数字调制分析
工商网监
评论