时间复杂度为O (nlogn)的排序算法简述
归并排序
归并排序遵循分治的思想：将原问题分解为几个规模较小但类似于原问题的子问题，递归地求解这些子问题，然后合并这些子问题的解来建立原问题的解，归并排序的步骤如下：
划分：分解待排序的 n 个元素的序列成各具 n/2 个元素的两个子序列，将长数组的排序问题转换为短数组的排序问题，当待排序的序列长度为 1 时，递归划分结束
合并：合并两个已排序的子序列得出已排序的最终结果
归并排序的代码实现如下：
private void sort(int[] nums, int left, int right) {
if (left >= right) {
return;
}
// 划分
int mid = left + right >> 1;
sort(nums, left, mid);
sort(nums, mid + 1, right);
// 合并
merge(nums, left, mid, right);
}
private void merge(int[] nums, int left, int mid, int right) {
// 辅助数组
int[] temp = Arrays.copyOfRange(nums, left, right + 1);
int leftBegin = 0, leftEnd = mid - left;
int rightBegin = leftEnd + 1, rightEnd = right - left;
for (int i = left; i <= right; i++) {
if (leftBegin > leftEnd) {
nums[i] = temp[rightBegin++];
} else if (rightBegin > rightEnd || temp[leftBegin] < temp[rightBegin]) {
nums[i] = temp[leftBegin++];
} else {
nums[i] = temp[rightBegin++];
}
}
}
归并排序最吸引人的性质是它能保证将长度为 n 的数组排序所需的时间和 nlogn 成正比；它的主要缺点是所需的额外空间和 n 成正比。 算法特性：
空间复杂度：借助辅助数组实现合并，使用 O (n) 的额外空间；递归深度为 logn，使用 O (logn) 大小的栈帧空间。忽略低阶部分，所以空间复杂度为 O (n)
非原地排序
稳定排序
非自适应排序
以上代码是归并排序常见的实现，下面我们来一起看看归并排序的优化策略：
将多次创建小数组的开销转换为只创建一次大数组
在上文实现中，我们在每次合并两个有序数组时，即使是很小的数组，我们都会创建一个新的 temp [] 数组，这部分耗时是归并排序运行时间的主要部分。更好的解决方案是将 temp [] 数组定义成 sort () 方法的局部变量，并将它作为参数传递给 merge () 方法，实现如下：
private void sort(int[] nums, int left, int right, int[] temp) {
if (left >= right) {
return;
}
// 划分
int mid = left + right >> 1;
sort(nums, left, mid, temp);
sort(nums, mid + 1, right, temp);
// 合并
merge(nums, left, mid, right, temp);
}
private void merge(int[] nums, int left, int mid, int right, int[] temp) {
System.arraycopy(nums, left, temp, left, right - left + 1);
int l = left, r = mid + 1;
for (int i = left; i <= right; i++) {
if (l > mid) {
nums[i] = temp[r++];
} else if (r > right || temp[l] < temp[r]) {
nums[i] = temp[l++];
} else {
nums[i] = temp[r++];
}
}
}
当数组有序时，跳过 merge () 方法 我们可以在执行合并前添加判断条件：如果nums[mid] <= nums[mid + 1] 时我们认为数组已经是有序的了，那么我们就跳过 merge () 方法。它不影响排序的递归调用，但是对任意有序的子数组算法的运行时间就变成线性的了，代码实现如下：
private void sort(int[] nums, int left, int right, int[] temp) {
if (left >= right) {
return;
}
// 划分
int mid = left + right >> 1;
sort(nums, left, mid, temp);
sort(nums, mid + 1, right, temp);
// 合并
if (nums[mid] > nums[mid + 1]) {
merge(nums, left, mid, right, temp);
}
}
private void merge(int[] nums, int left, int mid, int right, int[] temp) {
System.arraycopy(nums, left, temp, left, right - left + 1);
int l = left, r = mid + 1;
for (int i = left; i <= right; i++) {
if (l > mid) {
nums[i] = temp[r++];
} else if (r > right || temp[l] < temp[r]) {
nums[i] = temp[l++];
} else {
nums[i] = temp[r++];
}
}
}
对小规模子数组使用插入排序 对小规模数组进行排序会使递归调用过于频繁，而使用插入排序处理小规模子数组一般可以将归并排序的运行时间缩短 10% ~ 15%，代码实现如下：
/**
* M 取值在 5 ~ 15 之间大多数情况下都能令人满意
*/
private final int M = 9;
private void sort(int[] nums, int left, int right) {
if (left + M >= right) {
// 插入排序
insertSort(nums);
return;
}
// 划分
int mid = left + right >> 1;
sort(nums, left, mid);
sort(nums, mid + 1, right);
// 合并
merge(nums, left, mid, right);
}
/**
* 插入排序
*/
private void insertSort(int[] nums) {
for (int i = 1; i < nums.length; i++) {
int base = nums[i];
int j = i - 1;
while (j >= 0 && nums[j] > base) {
nums[j + 1] = nums[j--];
}
nums[j + 1] = base;
}
}
private void merge(int[] nums, int left, int mid, int right) {
// 辅助数组
int[] temp = Arrays.copyOfRange(nums, left, right + 1);
int leftBegin = 0, leftEnd = mid - left;
int rightBegin = leftEnd + 1, rightEnd = right - left;
for (int i = left; i <= right; i++) {
if (leftBegin > leftEnd) {
nums[i] = temp[rightBegin++];
} else if (rightBegin > rightEnd || temp[leftBegin] < temp[rightBegin]) {
nums[i] = temp[leftBegin++];
} else {
nums[i] = temp[rightBegin++];
}
}
}
快速排序 快速排序也遵循分治的思想，它与归并排序不同的是，快速排序是原地排序，而且快速排序会先排序当前数组，再对子数组进行排序，它的算法步骤如下：
哨兵划分：选取数组中最左端元素为基准数，将小于基准数的元素放在基准数左边，将大于基准数的元素放在基准数右边
排序子数组：将哨兵划分的索引作为划分左右子数组的分界，分别对左右子数组进行哨兵划分和排序
快速排序的代码实现如下：
private void sort(int[] nums, int left, int right) {
if (left >= right) {
return;
}
// 哨兵划分
int partition = partition(nums, left, right);
// 分别排序两个子数组
sort(nums, left, partition - 1);
sort(nums, partition + 1, right);
}
/**
* 哨兵划分
*/
private int partition(int[] nums, int left, int right) {
// 以 nums[left] 作为基准数，并记录基准数索引
int originIndex = left;
int base = nums[left];
while (left < right) {
// 从右向左找小于基准数的元素
while (left < right && nums[right] >= base) {
right--;
}
// 从左向右找大于基准数的元素
while (left < right && nums[left] <= base) {
left++;
}
swap(nums, left, right);
}
// 将基准数交换到两子数组的分界线
swap(nums, originIndex, left);
return left;
}
private void swap(int[] nums, int left, int right) {
int temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
}算法特性：
时间复杂度：平均时间复杂度为 O (nlogn)，最差时间复杂度为 O (n2)
空间复杂度：最差情况下，递归深度为 n，所以空间复杂度为 O (n)
原地排序
非稳定排序
自适应排序
归并排序的时间复杂度一直是 O (nlogn)，而快速排序在最坏的情况下时间复杂度为 O (n2)，为什么归并排序没有快速排序应用广泛呢？ 答：因为归并排序是非原地排序，在合并阶段需要借助非常量级的额外空间
快速排序有很多优点，但是在哨兵划分不平衡的情况下，算法的效率会比较低效。下面是对快速排序排序优化的一些方法：
切换到插入排序
对于小数组，快速排序比插入排序慢，快速排序的 sort () 方法在长度为 1 的子数组中也会调用一次，所以，在排序小数组时切换到插入排序排序的效率会更高，如下：
/**
* M 取值在 5 ~ 15 之间大多数情况下都能令人满意
*/
private final int M = 9;
public void sort(int[] nums, int left, int right) {
// 小数组采用插入排序
if (left + M >= right) {
insertSort(nums);
return;
}
int partition = partition(nums, left, right);
sort(nums, left, partition - 1);
sort(nums, partition + 1, right);
}
/**
* 插入排序
*/
private void insertSort(int[] nums) {
for (int i = 1; i < nums.length; i++) {
int base = nums[i];
int j = i - 1;
while (j >= 0 && nums[j] > base) {
nums[j + 1] = nums[j--];
}
nums[j + 1] = base;
}
}
private int partition(int[] nums, int left, int right) {
int originIndex = left;
int base = nums[left];
while (left < right) {
while (left < right && nums[right] >= base) {
right--;
}
while (left < right && nums[left] <= base) {
left++;
}
swap(nums, left, right);
}
swap(nums, left, originIndex);
return left;
}
private void swap(int[] nums, int left, int right) {
int temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
}
基准数优化 如果数组为倒序的情况下，选择最左端元素为基准数，那么每次哨兵划分会导致右数组长度为 0，进而使快速排序的时间复杂度为 O (n2)，为了尽可能避免这种情况，我们可以对基准数的选择进行优化，采用三取样切分的方法：选取数组最左端、中间和最右端这三个值的中位数为基准数，这样选择的基准数大概率不是区间的极值，时间复杂度为 O (n2) 的概率大大降低，代码实现如下：
public void sort(int[] nums, int left, int right) {
if (left >= right) {
return;
}
// 基准数优化
betterBase(nums, left, right);
int partition = partition(nums, left, right);
sort(nums, left, partition - 1);
sort(nums, partition + 1, right);
}
/**
* 基准数优化，将 left, mid, right 这几个值中的中位数换到 left 的位置
* 注意其中使用了异或运算进行条件判断
*/
private void betterBase(int[] nums, int left, int right) {
int mid = left + right >> 1;
if ((nums[mid] < nums[right]) ^ (nums[mid] < nums[left])) {
swap(nums, left, mid);
} else if ((nums[right] < nums[left]) ^ (nums[right] < nums[mid])) {
swap(nums, left, right);
}
}
private int partition(int[] nums, int left, int right) {
int originIndex = left;
int base = nums[left];
while (left < right) {
while (left < right && nums[right] >= base) {
right--;
}
while (left < right && nums[left] <= base) {
left++;
}
swap(nums, left, right);
}
swap(nums, originIndex, left);
return left;
}
private void swap(int[] nums, int left, int right) {
int temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
}
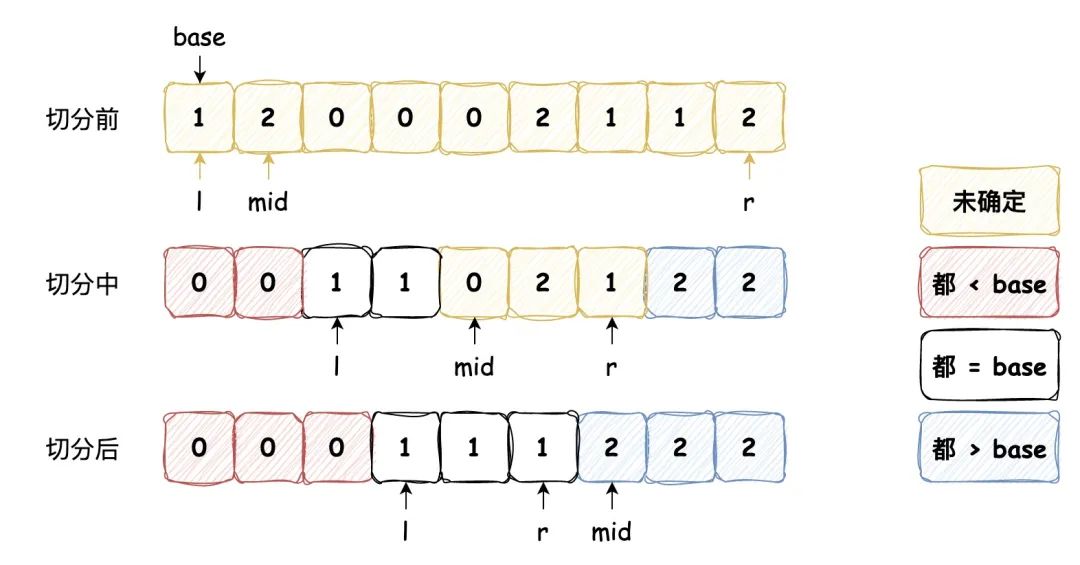
三向切分 在数组有大量重复元素的情况下，快速排序的递归性会使元素全部重复的子数组经常出现，而对这些数组进行快速排序是没有必要的，我们可以对它进行优化。 一个简单的想法是将数组切分为三部分，分别对应小于、等于和大于基准数的数组，每次将其中 “小于” 和 “大于” 的数组进行排序，那么最终也能得到排序的结果，这种策略下我们不会对等于基准数的子数组进行排序，提高了排序算法的效率，它的算法流程如下： 从左到右遍历数组，维护指针 l 使得 [left, l - 1] 中的元素都小于基准数，维护指针 r 使得 [r + 1, right] 中的元素都大于基准数，维护指针 mid 使得 [l, mid - 1] 中的元素都等于基准数，其中 [mid, r] 区间中的元素还未确定大小关系，图示如下：
public void sort(int[] nums, int left, int right) {
if (left >= right) {
return;
}
// 三向切分
int l = left, mid = left + 1, r = right;
int base = nums[l];
while (mid <= r) {
if (nums[mid] < base) {
swap(nums, l++, mid++);
} else if (nums[mid] > base) {
swap(nums, mid, r--);
} else {
mid++;
}
}
sort(nums, left, l - 1);
sort(nums, r + 1, right);
}
private void swap(int[] nums, int left, int right) {
int temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
}
这也是经典的荷兰国旗问题，因为这就好像用三种可能的主键值将数组排序一样，这三种主键值对应着荷兰国旗上的三种颜色
审核编辑：黄飞
声明：本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人，不代表德赢Vwin官网
网立场。文章及其配图仅供工程师学习之用，如有内容侵权或者其他违规问题，请联系本站处理。
举报投诉
-
算法
+关注
关注
23文章
4607浏览量
92826 -
数组
+关注
关注
1文章
417浏览量
25939
原文标题：时间复杂度为O (nlogn)的排序算法
文章出处：【微信号：OSC开源社区，微信公众号：OSC开源社区】欢迎添加关注！文章转载请注明出处。
发布评论请先 登录
相关推荐
常用的非比较排序算法：计数排序，基数排序，桶排序的详细资料概述
这篇文章中我们来探讨一下常用的非比较排序算法：计数排序，基数排序，桶排序。在一定条件下，它们的时间
如何求递归算法的时间复杂度
那么我通过一道简单的面试题，模拟面试的场景，来带大家逐步分析递归算法的时间复杂度，最后找出最优解，来看看同样是递归，怎么就写成了O(n)的代码。
算法时空复杂度分析实用指南2
类似的，想想之前说的数据结构扩容的场景，也许`N`次操作中的某一次操作恰好触发了扩容，导致时间复杂度提高，但总的时间复杂度依然保持在`O(N
算法时空复杂度分析实用指南（上）
本文会篇幅较长，会涵盖如下几点：
1、Big O 表示法的几个基本特点。
2、非递归算法中的时间复杂度分析。
3、数据结构 API 的效率衡量方法（摊还分析）。
算法时空复杂度分析实用指南（下）
Big O 表示法的几个基本特点。
2、非递归算法中的时间复杂度分析。
3、数据结构 API 的效率衡量方法（摊还分析）。
4、递归
如何计算时间复杂度
来完成，那么该算法的用处就不会太大。同样如果该算法需要若干个GB的内存，那么在大部分机器上都无法使用。 一个算法的评价主要从时间复杂度和空间
工商网监
评论