卡尔曼滤波是一种估计和预测系统状态的方法,通过将测量数据和系统模型结合,实现对系统状态的最优估计。它在控制、通信、导航等领域具有广泛应用。
卡尔曼滤波的核心思想是利用系统的动态方程和测量方程来不断更新系统状态的估计,同时考虑测量数据的不确定性和系统模型的误差。
卡尔曼滤波由五个基本公式组成,分别是预测状态、预测协方差、更新卡尔曼增益、更新状态和更新协方差。
第一个公式是预测状态的更新公式:
x(k|k-1) = F(k)x(k-1|k-1) + u(k)
其中,x(k|k-1)表示时刻k的状态的预测估计值,F(k)表示状态转移矩阵,x(k-1|k-1)表示时刻k-1的状态的估计值,u(k)表示控制量。
第二个公式是预测状态的协方差更新公式:
P(k|k-1) = F(k)P(k-1|k-1)F(k)^T + Q(k)
其中,P(k|k-1)表示时刻k的状态协方差的预测值,P(k-1|k-1)表示时刻k-1的状态协方差的估计值,Q(k)表示过程噪声的协方差矩阵。
第三个公式是更新卡尔曼增益的公式:
K(k) = P(k|k-1)H(k)^T(H(k)P(k|k-1)H(k)^T + R(k))^-1
其中,K(k)表示时刻k的卡尔曼增益,H(k)表示测量矩阵,R(k)表示测量噪声的协方差矩阵。
第四个公式是更新状态的公式:
x(k|k) = x(k|k-1) + K(k)(z(k) - H(k)x(k|k-1))
其中,x(k|k)表示时刻k的状态的估计值,z(k)表示时刻k的测量值。
第五个公式是更新状态协方差的公式:
P(k|k) = (I - K(k)H(k))P(k|k-1)
其中,I是单位矩阵。
卡尔曼滤波的过程可以分为两个步骤:预测和更新。预测步骤利用系统动态方程和控制量,通过前一时刻的状态估计值和协方差矩阵来预测当前时刻的状态估计值和协方差矩阵。更新步骤利用测量方程和测量值,通过预测的状态估计值和协方差矩阵来计算卡尔曼增益,并根据测量值来更新状态估计值和协方差矩阵。
卡尔曼滤波在实际应用中需要估计的状态和测量噪声的统计特性,以及系统的动态方程和测量方程。根据具体应用的不同,可以对卡尔曼滤波进行改进和扩展,例如扩展卡尔曼滤波、无迹卡尔曼滤波等。
总之,卡尔曼滤波是一种强大的状态估计方法,通过有效地利用测量数据和系统模型来实现对系统状态的最优估计。它的五个基本公式提供了实现卡尔曼滤波的框架,结合具体应用的需求和条件,可以对其进行改进和扩展,以适应不同的应用场景。
-
模型
+关注
关注
1文章
3226浏览量
48806 -
测量数据
+关注
关注
0文章
37浏览量
9176 -
卡尔曼滤波
+关注
关注
3文章
165浏览量
24648
发布评论请先 登录
相关推荐
卡尔曼滤波器介绍
【案例分享】四轴mpu6050姿态角卡尔曼滤波代码分析
通俗的讲解卡尔曼滤波的最基本的公式

经典卡尔曼滤波器的五个公式
如何理解卡尔曼滤波器?卡尔曼滤波器状态方程及测量方程
卡尔曼滤波(KF)与扩展卡尔曼(EKF)
什么是卡尔曼滤波?卡尔曼滤波的作用是什么
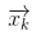
卡尔曼滤波的数学基础
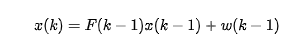




 卡尔曼滤波五个公式
卡尔曼滤波五个公式










评论