电感等效模型阻抗是电感元件在电磁场中对电流和电压的响应的量化描述。在电路分析和设计中,电感等效模型的阻抗对于预测和优化电路的性能至关重要。以下是电感等效模型阻抗公式的推导,以满足您的要求。
为了便于推导,假设电感元件是一个理想的线性元件,并且没有电阻和电容的影响。这个假设可以使我们专注于电感对电压和电流的响应。
首先,我们需要明确电感元件的定义。电感元件是由线圈或螺旋线缠绕而成,当通过这些线圈或螺旋线的电流变化时,会产生磁场。这个变化的电磁场会导致电感元件内部产生电动势。
根据法拉第定律,电动势的大小与磁场的变化率成正比。因此,我们可以得到电感元件的电动势表达式:
ε = -L * dI/dt
其中,ε是电动势,L是电感元件的电感,dI/dt是电流随时间的变化率。
我们知道,电感元件的电动势与电感元件两端的电压成正比。因此,我们可以得到电感元件的电压表达式:
V = -L * di/dt
其中,V是电感元件两端的电压,di/dt是电压随时间的变化率。
根据欧姆定律,电流和电压之间的关系可以表示为:
V = Z * I
其中,Z是电感元件的阻抗。将电感元件的电压表达式代入欧姆定律的公式中,我们可以得到:
-L * di/dt = Z * I
对上式两边同时求导,得到:
-L * d²i/dt² = Z * dI/dt
由于电感元件是线性元件,我们可以将上式重新写成常微分方程的形式:
d²i/dt² + (Z/L) * di/dt = 0
这是一个二阶常微分方程,描述了电流随时间的变化规律。为了解这个微分方程,我们可以假设电流变化的解形式为:
i(t) = I0 * exp(rt)
其中,I0是电流的初始值,r是待定的常数,exp(rt)是指数函数。
将上式代入常微分方程中,我们可以得到:
r² * I0 * exp(rt) + (Z/L) * r * I0 * exp(rt) = 0
化简后得到:
r² + (Z/L) * r = 0
这是一个二次方程,我们可以使用求根公式解得r的值。假设r1和r2是这个二次方程的两个解,那么电流变化的解形式可以写成:
i(t) = A * exp(r1t) + B * exp(r2t)
其中,A和B是待定的常数。
我们知道,电流应该是稳定的,即没有随时间的变化。因此,根据初始条件,我们可以得到:
di/dt = r1 * A * exp(r1t) + r2 * B * exp(r2t) = 0
由于exp函数在整个实数范围内都不会为0,因此我们可以得到:
r1 * A + r2 * B = 0
这是一个线性方程,我们可以使用矩阵求解的方法得到A和B的值。
综上所述,我们通过推导得到了电感等效模型阻抗的常微分方程和解形式。这个模型可以用来描述电感元件在电路中的行为和对电流和电压的响应。
-
线圈
+关注
关注
14文章
1820浏览量
44426 -
电感
+关注
关注
54文章
6136浏览量
102294 -
电动势
+关注
关注
6文章
244浏览量
16328 -
电感元件
+关注
关注
0文章
68浏览量
10086
发布评论请先 登录
相关推荐
求射极偏置共射放大电路交流等效电路的Z0和Av公式推导。
LLC增益曲线过程推导和参数如何计算
电动助力转向EPS——理论公式推导及simulink模型
基于粒子模拟的磁绝缘传输线等效电容和等效电感的计算
电感阻抗计算公式
撬棒保护的DFIG等效序阻抗
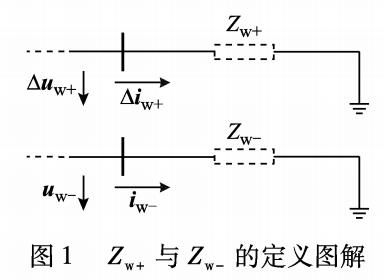




 电感等效模型阻抗公式推导
电感等效模型阻抗公式推导












评论