Arm Helium 技术诞生的由来
克服 Amdahl 定律的影响
在前几篇文章中,我们介绍了采用 Arm Helium 技术(也称为 MVE)的 Armv8.1-M 架构如何处理矢量指令。但问题是,每当代码被矢量化时,Amdahl 定律的影响很快便会显现,让人措手不及。如果您不了解 Amdahl 定律,可以简单理解为,Amdahl 定律表明算法中无法并行化的部分很快就会成为性能瓶颈。例如,如果有 50% 的工作负载可以并行化,那么即使这部分工作负载可以无限并行,最多也只能将速度提高二倍。不知您作何感受,如果我能将某件事情无限并行化,但速度却只能提升二倍,这种微不足道的提升一定会让我感到非常恼火!在设计 Helium 时,我们必须考虑矢量指令及其相关联的一切内容,这样才能最大限度地提高性能。
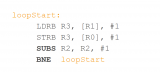
串行代码在循环处理中很常见,串行代码造成的开销可能相当大,特别是对于小循环。下面的内存复制代码就是一个很好的例子:

循环迭代计数的递减和返回循环顶端的条件分支占循环指令的 50%。许多小型 Cortex-M 处理器没有分支预测器(小型 Cortex-M 处理器的面积效率极高,这意味着许多分支预测器比整个 Cortex-M 处理器还要大几倍)。因此,由于分支损失,运行时开销实际上高于 50%。通过在多次迭代中摊销开销,循环展开可以帮助减少开销,但会增加代码大小,并使代码的矢量化过程更加复杂。
鉴于许多 DSP 内核都有小循环,因此在 Helium 研究项目中解决这些问题至关重要。许多专用 DSP 处理器支持零开销循环。一种实现方法是使用 REPEAT 指令,告诉处理器将下面的指令重复 N 次:

处理器必须记录多项数据:
循环开始的地址
需要分支回到循环开始前所剩余的指令数
剩余的循环迭代次数
在处理中断时,跟踪记录所有这些数据可能会造成问题,因此一些 DSP 只需要延迟中断,直到循环完成。如果要执行大量的迭代,这可能需要相当长的时间,而且完全不符合 Cortex-M 处理器应该实现的快速和确定性中断延迟的需求。这种方法也不适用于处理精确故障,如权限违规导致的内存管理故障异常 (MemManage)。另一种方法是增加额外的寄存器来处理循环状态。但这些新寄存器必须在异常进入和返回时保存和恢复,而这又会增加中断延迟。为了解决这个问题,Armv8.1-M 采用了一对循环指令:

该循环首先执行 While Loop Start (WLS) 指令,该指令将循环迭代计数复制到 LR,循环迭代计数为零时,分支到循环结束。还有一条 Do Loop Start (DLS) 指令,可用于设置一个循环,在该循环中至少始终执行一次迭代。Loop End (LE) 指令检查 LR 以确认是否还需要一次迭代,如果需要,则分支返回起点。有趣的是,处理器可以缓存 LE 指令提供的信息(即循环开始和结束的位置),因此在下一次迭代时,处理器甚至可以在获取 LE 指令之前分支回到循环的起点。因此,处理器执行的指令序列如下所示:

在循环末尾添加循环指令有一个很好的副作用,如果缓存的循环信息刷新,该指令将重新执行。然后,重新执行 LE 指令将重新填充缓存。如下图所示,由于无需保存循环开始和结束地址,因此现有的快速中断处理功能得以保留。

除了第一次迭代和从中断恢复时的一些设置外,所有时间实际上都花在了内存复制而不是循环处理上。此外,由于处理器事先知道指令的顺序,因此总能用正确的指令填充流水线。这样就消除了流水线清空和由此导致的分支损失。因此,我们可以将这一循环矢量化,不必再担心 Amdahl 定律的影响,我们(暂时)克服了这些困难。
在对代码进行矢量化时,一个循环通常以不同类型的指令开始和结束,例如矢量加载 (VLDR) 和矢量乘加 (VMLA)。执行这样的循环时,会产生一长串不间断的交替 VLDR/VMLA 操作(如下图所示)。这种不间断的链条使处理器能够从指令重叠中获得最大益处,因为它甚至可以从一个循环迭代结束重叠到下一个迭代开始,从而进一步提高性能。关于指令重叠的更多信息,可参阅:《Arm Helium 技术诞生的由来:为何不直接采用 Neon?》

当需要处理的数据量不是矢量长度的倍数时,矢量化代码就会出现问题。典型的解决方案是先处理全矢量,然后用一个串行/非矢量化尾部清理循环来处理剩余的元素。不知不觉中,Amdahl 定律又出现了,真是令人不胜其烦!Helium 中的矢量可容纳 16 个 8 位数值,因此在我们对 31 字节的 memcpy 函数进行矢量化时,仅有不到一半的拷贝将由尾部循环连续执行,而不是由矢量指令并行执行。
为了解决这个问题,我们增加了循环指令的尾部预测变体(如 WLSTP、LETP)。对于这些尾部预测循环,LR 保存的是要处理的矢量元素的个数,而不是要执行的循环迭代的次数。循环开始指令 (WLSTP) 有一个大小字段(下面 memcpy 函数示例中的“.8”),用于指定要处理的元素的宽度。

如果您曾见过其他优化的 memcpy 例程,可能会对这个例子的简单程度感到惊讶,但对于 Helium 来说,这已经是最好的完全矢量化解决方案所需要的一切了。具体工作原理如下:处理器使用大小字段和剩余元素的数量来计算剩余迭代次数。
如果最后一次迭代要处理的元素个数少于矢量长度,则矢量末尾相应数量的元素将被禁用。因此,在上文复制 31 个字节的例子中,Helium 会在第一次迭代时并行复制 16 个字节,然后在下一次迭代时并行复制 15 个字节。这不仅可以避免 Amdahl 定律的影响,实现该有的性能,还可以完全消除串行尾码,减少代码量,简化开发过程。
由于面临高性能目标和严格的面积/中断延迟限制,我们在设计 Helium 时就像在设计一个多维拼图,且其中一半的形状是已经固定的。架构中看似毫不相干的部分可以相互作用,产生意想不到的效果或助力解决一些有趣的难题。
整个 Helium 研究团队和我都无比期待看到 Helium 技术能够为全新的应用带来有力的支持。目前 Cortex-M 已有三款产品支持 Helium 技术——Cortex-M52、Cortex-M55 和 Cortex-M85,我迫不及待看到 Helium 技术持续赋能我们生态伙伴的 AI 创新应用。
审核编辑:刘清
-
处理器
+关注
关注
68文章
19259浏览量
229647 -
dsp
+关注
关注
553文章
7987浏览量
348728 -
寄存器
+关注
关注
31文章
5336浏览量
120224 -
ARM技术
+关注
关注
0文章
22浏览量
7286 -
Cortex-M
+关注
关注
2文章
229浏览量
29752
原文标题:Helium 技术讲堂 | 克服 Amdahl 定律的影响
文章出处:【微信号:Arm社区,微信公众号:Arm社区】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
欧姆定律与电路分析技巧
欧姆定律的实际应用实例
欧姆定律的常见误区
欧姆定律和基尔霍夫定律的区别
什么定律体现了线性电路元件上电压 欧姆定律在实际电路中的应用
如何克服阿姆达尔(Amdahl)定律的影响?




 如何克服Amdahl定律的影响呢?
如何克服Amdahl定律的影响呢?










评论