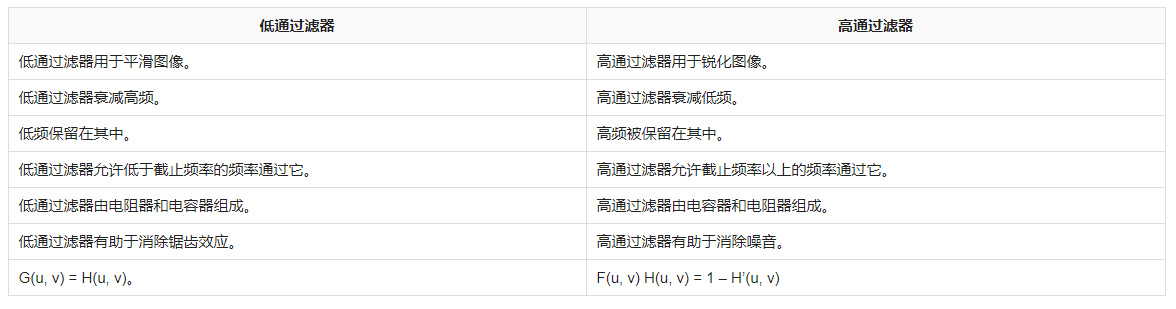
低通滤波器电路是一种能够通过滤除高频信号而通过低频信号的电路。它广泛应用于信号处理、音频放大和通信系统中,用于去除噪音和不需要的高频成分。低通滤波器的设计和传递函数计算是相关电子学和信号处理课程中的重要内容。下面,我将详细介绍低通滤波器的电路特点及传递函数的计算方法。
首先,我们来了解一下低通滤波器的电路特点。
- 频率响应:低通滤波器具有截止频率,高于截止频率的信号会被滤除,而低于截止频率的信号会通过。这意味着低通滤波器可以去除高频成分,仅保留低频成分。
- 幅频特性:低通滤波器在通过低频信号时幅度基本保持不变,而随着频率的增加,幅度逐渐下降。这种幅频特性使得低通滤波器可以用于音频放大器中,使音频信号放大时不会产生失真。
- 相频特性:低通滤波器会引入相位延迟,随着频率的增加,相位延迟会逐渐增加。这对于某些特定应用,如音频信号处理和通信系统是非常重要的。
- 阶数:低通滤波器的阶数决定了其频率选择性能和幅度下降速度。阶数越高,滤波器的选择性和幅度下降速度越大。
接下来,我们将介绍低通滤波器传递函数的计算方法。
传递函数是指输入信号和输出信号之间的数学关系,用于描述滤波器的工作原理。在信号处理中,传递函数通常以频域表达,也称作频域传输特性。
低通滤波器的传递函数可以用各种方式表示,包括巴特沃斯(Butterworth)、切比雪夫(Chebyshev)、椭圆(Elliptic)等。下面,我们以巴特沃斯滤波器为例,介绍传递函数的计算方法。
巴特沃斯滤波器是一种优化了幅度特性和相频特性的低通滤波器。其传递函数公式为:
H(s) = 1 / (1 + (s/Wc)^2N)^0.5
其中,H(s)为传递函数,s为复频率变量,Wc为截止频率,N为滤波器的阶数。
传递函数中的复频率变量s可以表示为s = jω,其中j为虚数单位,ω为角频率。将s替换为jω,并对传递函数进行数学运算,最终可以得到传递函数的频域表达式。
通过计算传递函数的频域表达式,可以获得低通滤波器在不同频率下的增益和相位特性。这些特性可以用来分析和设计低通滤波器,以满足特定应用的要求。
除了巴特沃斯滤波器,切比雪夫和椭圆滤波器也有相应的传递函数表达式,具体计算方法类似,但是形式略有不同。针对不同的应用场景和性能需求,可以选择合适的滤波器类型和相应的传递函数表达式进行设计。
总结起来,低通滤波器是一种能够通过滤除高频信号而通过低频信号的电路,具有频率响应、幅频特性、相频特性和阶数等特点。传递函数是用于描述滤波器输入输出关系的数学表达式,可以通过不同滤波器类型的特定公式来计算。
-
低通滤波器
+关注
关注
14文章
474浏览量
47384 -
通信系统
+关注
关注
6文章
1187浏览量
53322 -
函数
+关注
关注
3文章
4327浏览量
62567 -
低频信号
+关注
关注
2文章
47浏览量
8310
发布评论请先 登录
相关推荐
无源低通滤波器电路,有源低通滤波器原理图
四种低通滤波器的电路分析
低通滤波器传递函数
LC低通滤波器作用及应用案例
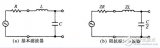
基于使用双极点RC低通滤波器推导代数传递函数
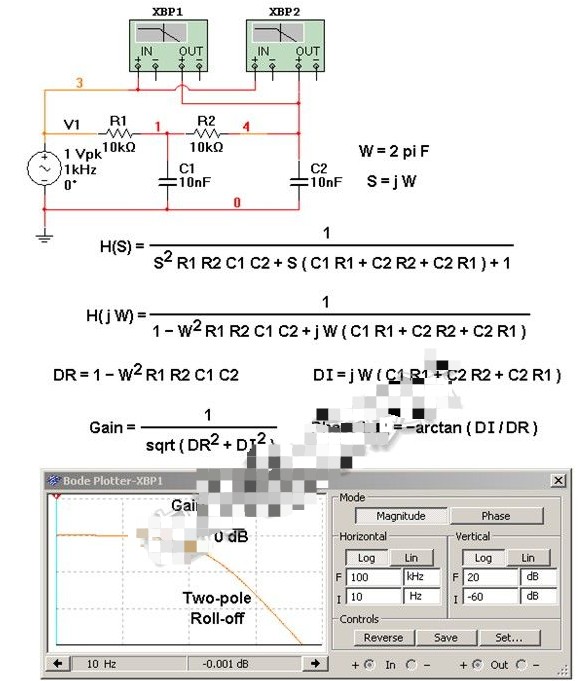
低通滤波器电路图分享




 低通滤波器电路特点 低通滤波器传递函数怎么算
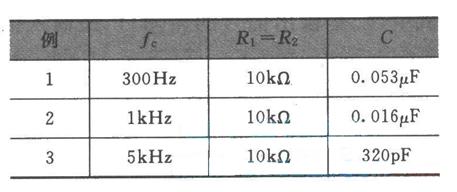
低通滤波器电路特点 低通滤波器传递函数怎么算


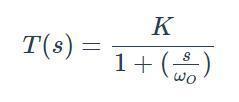











评论