摘要
量子点半导体光放大器(QD-SOA)具有全光信号处理和光信号再生等突出特点,在光通信系统中得到了广泛的应用。由于这些放大器的纳米结构,它们的精确设计和建模是一个复杂而具有挑战性的问题。本文讨论了QD-SOA的设计,提出了一种基于遗传算法的QD-SOA设计新方法。由于具有用于设计的模型是必不可少的,因此在第一步中获得数值模型。然后,利用从数值模型中采样的训练数据建立人工神经网络模型。实验表明,该神经模型具有较高的精度和较低的计算时间。在下一步中,我们将设计问题转化为遗传算法问题。利用神经模型,定义了合适的拟合函数。用户可以通过设置设计参数的权重来优化生产成本。所提出的系统找到了满足关于生产成本的期望增益的最佳解决方案。
1. 引言
目前,量子点半导体光放大器(QD-SOA)被用于光纤通信网络中的高速放大和全光信号处理。QD-SOA包含具有量子机械与光相互作用的纳米结构层[1]-[2]。
量子点半导体光放大器(SOA)对光信号的放大理论是基于处理电-光相互作用和光脉冲传播的密度矩阵方程[3]。这让QD-SOA的设计非常复杂。因此,通过智能方法优化SOA设计是非常有益的。遗传算法(GA)在考虑期望增益的情况下确定模型输入的最优量。对于这种设计,有一个人工神经网络(ANN)模型和数值数据是至关重要的。本文设计了一种具有期望增益的QD-SOA。QD-SOA的优化设计尚未有文献报道。
本文内容如下:第2节介绍了QD-SOA的ANN模型;第三节介绍了遗传算法的优化设计;第4节包含结论。
2.QD-SOA-ANN模型
人工神经网络基于数值数据的计算来学习一般规则。神经网络中最小的部分是神经元。在图1中,给出了神经元的示意图。它接收来自其他一些神经元的输入,或者可能来自外部来源。每个输入x具有相关联的权重w,该权重可以被修改以对学习进行建模。神经元计算其输入的加权和的一些函数f:

f是传递函数。一种常见的传递函数是S形函数,该函数是神经网络中经常用于在模型中引入非线性和/或确保某些信号保持在指定范围内的数学函数。Sigmoid函数由以下公式定义:

神经网络最常见的结构是多层前馈网络。在前馈神经网络中,神经元以层的形式组织。一层中的神经元从上一层获得输入,并将其输出提供给下一层。在这种网络中,不允许连接到相同或先前层中的神经元。神经元的最后一层称为输出层,输入层和输出层之间的层称为隐藏层。输入层由特殊的输入神经元组成,仅将施加的外部输入传输到其输出。
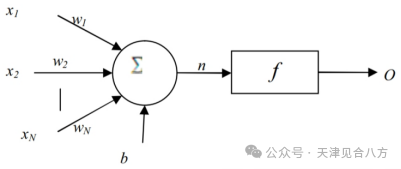
图1神经元示意图
在一个网络中,如果只有一个或多个隐藏层,这种网络称为多层网络。反向传播算法已成为设计一类特殊的分层前馈网络(称为多层感知器)的主力。
第一步,我们收集了1.3μm波长的InAs/GaAs量子点SOA的数据。为此,通过数值方法对上述QD-SOA进行了建模。有关QD-SOA数值模型的详细信息,请参阅[4]。提出了一种人工神经网络模型。经过几次尝试并趋向于更简单的模型,选择了一种具有一个隐藏层、四个输入和一个输出的前馈神经网络。该ANN模型的输入是器件的长度、有源介质的有效厚度、施加的电流密度和约束因子,输出是放大器增益。该模型中使用的算法是反向传播算法,因为上述算法不需要非常精确的数据。所获得的数据分为3部分:训练数据集、检查数据集和测试数据集。通过训练数据集对神经网络模型进行训练。检查数据集用于防止过拟合。测试数据集用于评价神经网络模型。隐藏层和输出层中的传递函数分别是Sigmoid函数和Pure line函数。
我们在隐藏层中使用不同的神经元来训练前馈神经网络模型。性能指数为均方误差。由于神经网络的非最优响应和收敛到局部极小值,神经网络被多次训练,训练数据没有得到定期处理。在这种情况下,我们获得了最好的响应。在表1中,显示了训练ANN的一些结果。
表1非精细训练数据和不同神经元的结果
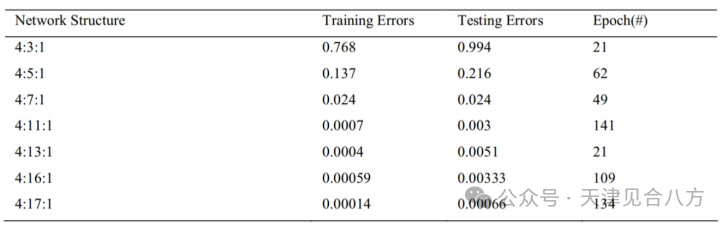
可以看出,对于隐藏层中有17个神经元的ANN,获得了最好的结果。在该模型中,测试数据的均方误差小于0.0007,表明该模型具有较高的精度。
3.遗传算法优化设计
遗传算法是基于达尔文理论的优化算法。它们对设计参数的编码版本进行操作,而不是直接对这些参数本身进行操作。基本上,遗传算法选择设计参数作为“母本”,通过重组亲本参数中的组件来形成“后代”。后代取代系统中的弱参数,进入竞争,在满足条件时被激活和测试[5]。因此,一种粗略但高速的遗传算法vwin 了进化背后的遗传过程。
在本研究中,目的是设计具有所需增益的放大器。为了达到这一目的,需要考虑所需增益来优化有效参数。这意味着有效的参数被优化,而它以最小的成本获得期望的增益。这种方法使用了遗传算法。
在建立模型并定义合适的神经网络结构用于参数优化后,该方法是通过MATLAB软件的GA工具箱来获得所需的增益。首先定义了问题的变量和适应度函数。问题的变量与神经网络模型的输入相同。给出了拟合公式:

如图所示,适合度函数包含两个术语。第一项与算法误差有关,其中h为:

和

其中GActual是实际增益,GDesired是从适当的ANN模型获得的期望增益。第二个术语与有效参数有关,称为成本函数。给出了成本函数:
 其中,xi是算法的变量(ANN建模中的4个输入参数),wi是变量的相关权重。wi取决于制造商的条件。这意味着更重要(成本更高)的变量具有更大的权重。在拟合函数中,如果实际增益大于期望增益,则省略第一项,仅成本函数变得重要。拟合函数的第一项和第二项的值是通过为v选择合适的值来定义的。
其中,xi是算法的变量(ANN建模中的4个输入参数),wi是变量的相关权重。wi取决于制造商的条件。这意味着更重要(成本更高)的变量具有更大的权重。在拟合函数中,如果实际增益大于期望增益,则省略第一项,仅成本函数变得重要。拟合函数的第一项和第二项的值是通过为v选择合适的值来定义的。
在本研究中,利用MATLAB软件中的GA工具箱,获得了17个神经元的神经网络的实际增益,并进行了确定优化有效参数的实验。首先,通过连续实验,得到了最佳的拟合函数和v值。当轮盘是选择函数,第一种群和交叉分别为40和0.8,并且在最佳条件下,v的值在100到400之间时,实现了最优设计。然后,对于不同的权重,重复实验。这些实验的结果如表2所示。
表2遗传算法设计QD-SOA的结果
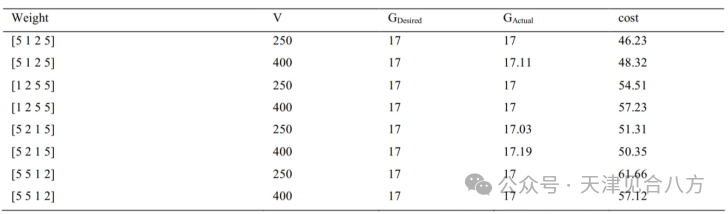
根据实验,当v值为250,权重为[5 1 2 5]时,达到了最佳拟合。一般来说,在考虑期望增益的情况下,遗传算法在QD-SOA中具有找到有效参数最优值的适当潜力。
4.结论
在这项工作中,提出了一种新的方法来确定考虑期望增益的最优模型输入量。这种方法使用了遗传算法。根据遗传算法的实验,确定了最优设计的最佳选择函数、交叉函数和第一种群,得到了最佳适应度函数的估计值v。一般来说,所提出的方法在考虑期望增益的材料成本方面给出了合适的结果。
参考文献
1. A.J. Zilkie et al, "Carrier Dynamics of Quantum-Dot, Quantum-Dash, and Quantum-Well Semiconductor Optical Amplifiers Operating at 1.55 ȝm", IEEE, No. 11 (2007) 43, p-p. 982.991.
2. A. Bilenca et al, "Broad-Band Wavelength Conversion Based on Cross-Gain Modulation and Four-Wave Mixing in InAs–InP QuantumDash Semiconductor Optical Amplifiers Operating at 1550 nm", IEEE, No. 4 (2003) 15, p.p. 563-565.
3. M. Sugawara et al, "Theory of Optical Signal Amplification and Processing by Quantum-Dot Semiconductor Optical Amplifiers", PHYSICAL REVIEW, B, 69(23),235332(39), (2004).
4. F.Hakimiyan et al," Modeling Quantum Dot Semiconductor Optical Amplifier Using Artificial Neural Network", presented in 3rd International Congress on Nanoscience and Nanotecnology(ICNN2010), held by Shiraz University in co-operation with the Iranian Nano Society(INS). 5. R. Haupt et al, Practical Genetic Algorithm, Wiley, New Jersy, 2004.
注:本文由天津见合八方光电科技有限公司挑选并翻译,旨在推广和分享相关SOA半导体光放大器基础知识,助力SOA技术的发展和应用。特此告知,本文系经过人工翻译而成,虽本公司尽最大努力保证翻译准确性,但不排除存在误差、遗漏或语义解读导致的不完全准确性,建议读者阅读原文或对照阅读,也欢迎指出错误,共同进步。
-
神经网络
+关注
关注
42文章
4771浏览量
100703 -
遗传算法
+关注
关注
0文章
237浏览量
20610 -
ANN
+关注
关注
0文章
22浏览量
9197
原文标题:用AI设计QD SOA
文章出处:【微信号:天津见合八方,微信公众号:天津见合八方】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
一种降低VIO/VSLAM系统漂移的新方法
大华股份荣获2024年中国创新方法大赛一等奖
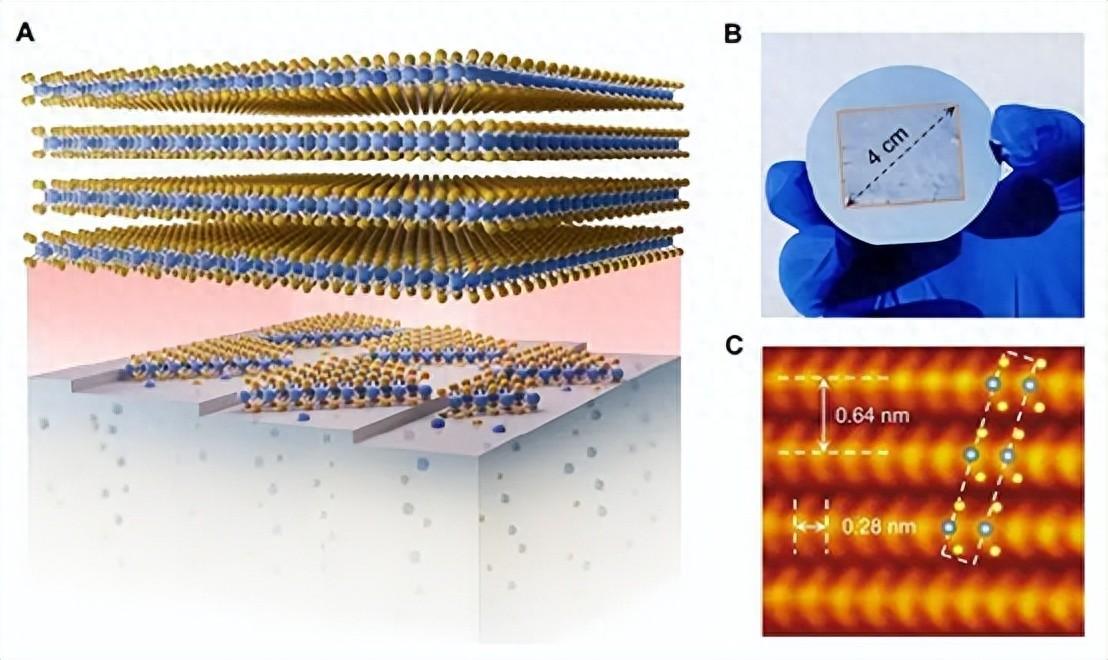
利用全息技术在硅晶圆内部制造纳米结构的新方法
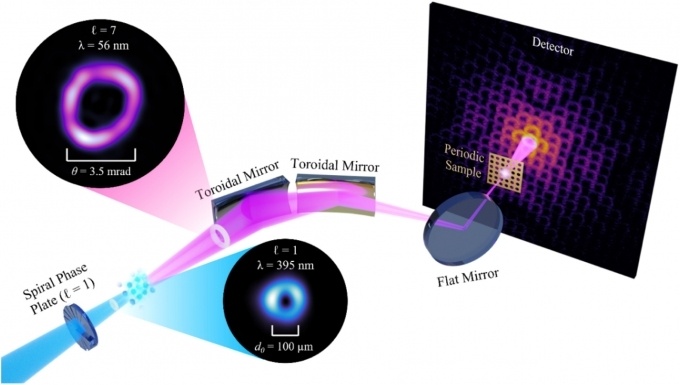
上海光机所提出强激光产生高能量子涡旋态电子新方法

一种无透镜成像的新方法
从“盖房子”到“顶竹笋”:我国科学家首创晶体制备新方法

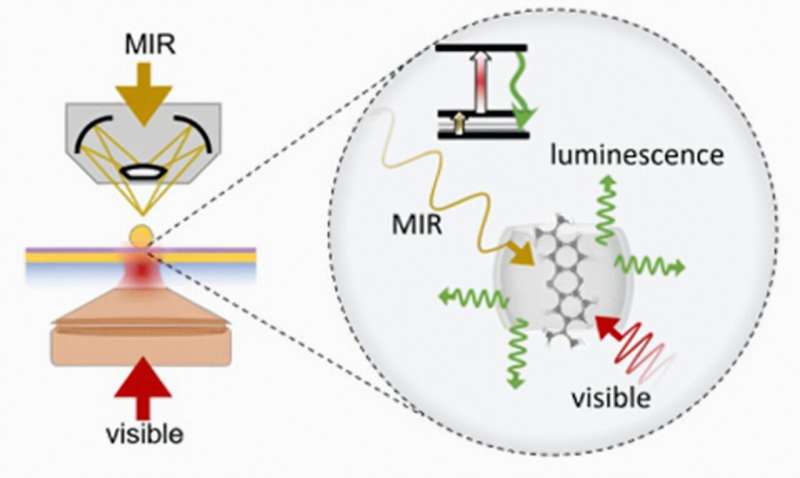
使隐形可见:新方法可在室温下探测中红外光
功率模块铜线键合工艺参数优化设计方案




 基于遗传算法的QD-SOA设计新方法
基于遗传算法的QD-SOA设计新方法












评论