今天来学习波特图,对于很多闭环系统,我们需要画出其波特图去分析其稳定性,而且一个系统动静态性能的好坏可以从波特图中直观的体现出来。在讲解波特图之前,我们先来回顾一下复数知识,下图为复平面,即以实部为x轴和虚部为y轴的坐标系。给定一个复数,我们可以通过以下两个公式求出其模和幅角,而且分贝概念的定义就是20倍的增益的模取以10为底的对数。这里选择对数的原因为可以在有限的坐标下包含更大的频率范围。

接下来,再来看一下一阶系统的波特图,首先给出一阶系统的传递函数,并且取其模,这里对分数取模等于对分子分母分别取模再相除,再取对数得到增益的分贝形式,这里直流增益为0dB,还可以得到其角度,右下图为二阶系统的波特图,但是我们可以只看其低频部分(<100kHz),在频率非常底的时候(<1Hz),系统增益为直流增益,而对于RC一阶滤波系统来说,直流增益为0dB,频率在大于第一个极点时,增益以每十倍频程-20dB下降,幅角为-45度,在之后将降低到-90度。

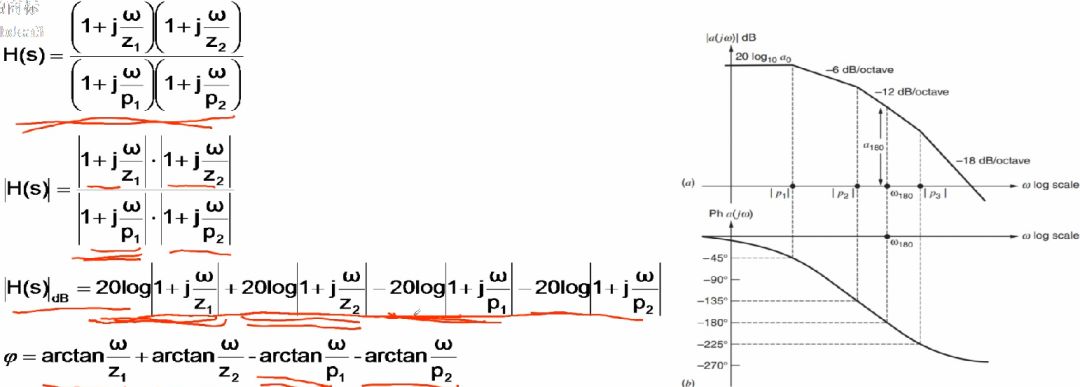
接下来,再来讲解二阶系统的波特图,同样的,我们先来回顾一下数学知识,利用欧拉公式能够简化复数的乘法和除法运算,通过下式观察可知,复数相乘,结果的模为两个乘数的模的乘积,结果的幅角为两个乘数幅角的和。同理,复数相除,其模相除,其幅角相减。

这样我们在计算二阶系统的模和幅角就会方便的多,首先将传递函数分子分母因式分解得到下式,再对其取模,这里可以先用除法关系,这样模为分子分母模的商,再利用乘法关系,这样模为各个因式的模,幅角同理,为分子各因式幅角的和再减去分母各因式的幅角。这样就可以画出其波特图,再来看右边的波特图,在第一个极点之后,增益以-20dB每十倍频下降(图中为-6dB每倍频下降,但下降速率是相同的),相角下降到-45度,之后在无穷远处下降到-90度,在第二个极点之后,增益以-40dB每十倍频下降,相角下降到-135度,之后在无穷远处下降到-180度。总结一下,极点的作用就是,在增益上面,改变极点频率之后的斜率,每经过一个极点之后增益下降速率增加-20dB每十倍频程,而在相角方面,对相角的改变是逐渐产生的,具体体现在每经过一个极点之后角度由前一个角度逐渐减小45度,并在之后再逐渐减小45度。零点与之类似,其作用就是,在增益上面,改变零点频率之后的斜率,每经过一个零点之后增益上升速率增加20dB每十倍频程,而在相角方面,对相角的改变是逐渐产生的,具体体现在每经过一个极点之后角度由前一个角度逐增加45度,并在之后再逐渐增加45度。可以看出,零极点的作用相反,所以采用增加零点或极点的方式抵消掉极点或零点来对系统进行校正。

当电阻和电容串联时会产生一个零点和零极点。

下面再对下面电路的波特图进行分析,也是运放电路常用的一种形式,先从阻抗的角度进行分析,得到会产生一个低频极点和高频零点。这里零点和极点的定义是让每个因式为零的S的解,再从反馈的角度进行分析,产生的是一个高频极点和低频零点。

-
波特图
+关注
关注
1文章
28浏览量
11218 -
传递函数
+关注
关注
0文章
101浏览量
13854
原文标题:运放提高笔记第20集-波特图讲解
文章出处:【微信号:yingjiansanrenxing,微信公众号:硬件三人行】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐




 一个系统动静态性能的好坏可以从波特图中直观的体现出来
一个系统动静态性能的好坏可以从波特图中直观的体现出来










评论