Linear Programming线性规划,就是目标函数和约束条件都是线性的优化问题,是运筹学中研究较早、发展较快、应用广泛、方法较成熟的一个重要分支,它是辅助人们进行科学管理的一种数学方法,英文缩写LP。
一、业务问题描述:这是一个简单的线性规划问题,具体要求如下:
某公司生产氨气(NH3)和氯化铵(NH4CI), 公司的日处理能力为50单位的氮(N), 180单位的氨(H), 40单位氯(CI). 氨气的利润为30$/每单位、氯化铵的利润为40$/每单位,如何确定氨气和氯化铵的产量,使利润最大?
二、从数学的角度理解和定义该问题:
将上述生产问题转为为数学问题,建立数学模型一般有以下三个步骤:
1.根据影响所要达到目的的因素找到决策变量;
2.由决策变量和所在达到目的之间的函数关系确定目标函数;
3.由决策变量所受的限制条件确定决策变量所要满足的约束条件。
三、OPL模型建立的步骤
下面用OPL语言来理解和定义该问题,OPL模型就是寻找决策变量,使得决策变量满足约束条件并取得目标函数最值的过程。下面是求解该问题的几个步骤:
1.定义该问题的数据变量,
为了方便起见,以下定义的数据变量均为数组变量,数组是有序数据的集合,一个数组中的每一个元素都属于同一种数据类型。
(1)Products 代表气体的名称,
{string}Products = ...;
即定义了数组名为“Products”的字符串数组,一维数组。
(2)Components 代表所含的成分,
{string} Components = ...;
即定义了数组名为“Components”的字符串数组,一维数组。
(3)Demand 代表每种气体所含的成分,
floatDemand[Products][Components] = ...;
即定义了数组名为“Demand”的浮点型数组,二维数组。
(4)Profit 代表对应气体的利润,
float Profit[Products] =...;
即定义了数组名为“Profit”的浮点型数组,一维数组。
(5)Stock 代表该成分的日处理能力,
float Stock[Components] =...;
即定义了数组名为“Stock”的浮点型数组,一维数组。
2.数据的初始化;
定义了数据变量之后,要进行数据的初始化,所谓初始化就是给数据变量赋值,下面依次给上述定义的数据变量赋值:
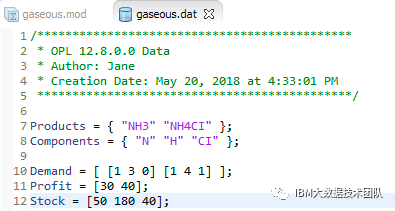
Products = { "NH3" "NH4CI"};
Components = { "N" "H" "CI"};
Demand = [ [1 3 0] [1 4 1] ];
Profit = [30 40];
Stock = [50 180 40];
3.定义决策变量,数据变量和决策变量是有区别的,数据变量是具体数据的名称,比如之前定义的数据变量“Products”,代表该公司生产气体的名称,而决策变量是针对数学模型来说的,这个问题所需做的决策即每种气体的产量,
dvar float+Production[Products];
dvar(decision variable)是定义决策变量的一个最常用的关键字,
此处定义了变量名为”Production”的决策变量,代表两种气体的产量,其实是浮点型数组。
4. 目标函数的定义,即利润最大化,目标函数是决策变量的线性函数,
maximize
sum( p in Products )
Profit[p] * Production[p];
5. 约束条件的设定,有三种成分有日处理能力的限制,用很简洁的写法实现:
subject to {
forall( c in Components )
ct:
sum( p in Products )
Demand[p][c] * Production[p] <= Stock[c];
}
四、用IBM ILOG CPLEX Optimization Studio 12.8来求解该问题
IBM ILOG CPLEX Optimization Studio 12.8来求解该问题的具体操作过程如下:
打开软件界面,有四个常用的窗口,分别是OPL项目导航窗口、编辑窗口、问题浏览器窗口、输出窗口;
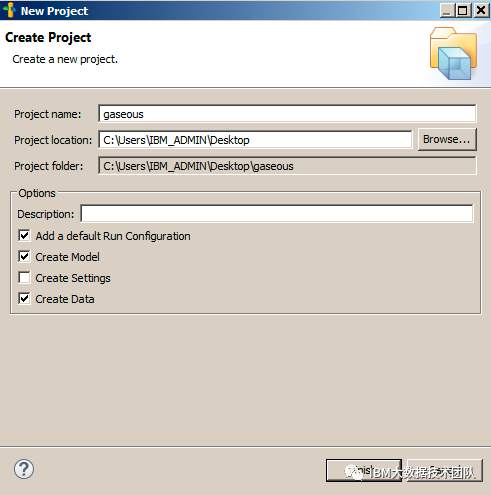
新建一个OPL项目,项目名称是“gaseous”,勾选”Adda default Run Configuration”、“CreateModel”和“CreateData”,即该OPL项目包含一个模型文件和一个数据文件;
编辑模型文件的内容,即“gaseous.mod”文件
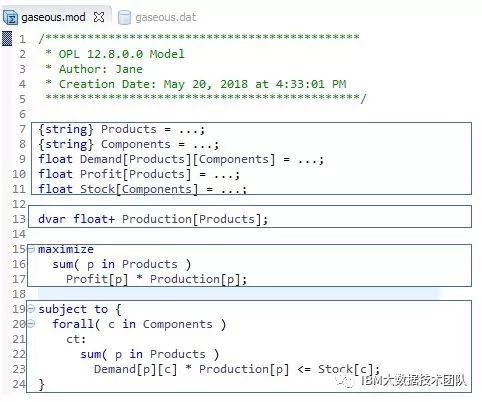
该模型文件的内容包含四部分内容:
(1) 定义数据变量;
(2) 定义决策变量;
(3) 设定目标函数;
(4) 设定约束条件;
编辑数据文件的内容,即“gaseous.dat”文件
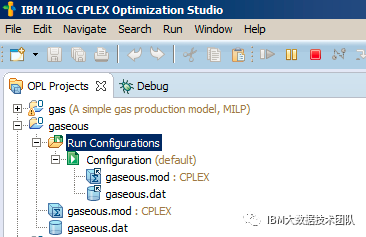
然后在”Configuration(default)”上执行:
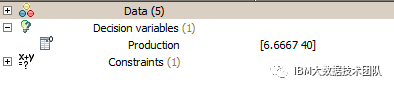
执行 Run Configuration,得到如下输出结果:
五、业务解读
从IBM ILOG CPLEX Optimization Studio 12.8的运行结果,可知当氨气的产量为6.6667个单位,氯化铵的产量为40个单位时,该公司得到最大利润,并满足当日每种成分的处理能力限制。
-
IBM
+关注
关注
3文章
1755浏览量
74677 -
线性
+关注
关注
0文章
198浏览量
25145
原文标题:IBM ILOG CPLEX Optimization Studio : 一个线性规划的案例
文章出处:【微信号:SCAnalyticsPlatform,微信公众号:IBM大数据技术团队】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
用MATLAB优化工具箱解线性规划
matlab数学建模算法全收录 799*** 4.7M 超清书签版
基于整数线性规划的TTA代码优化
线性规划在缓冲区溢出检测中的应用研究
数学建模教程之线性规划的详细说明
复杂施工调度问题的混合整数线性规划模型
如何在MATLAB中使用线性规划求解不同的问题
使用内点法求解线性规划问题
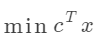




 一个简单的线性规划问题
一个简单的线性规划问题










评论