深度学习算法背后的数学

Python软件基金会成员（Contibuting Member）Vihar Kurama简要介绍了深度学习算法背后的数学。

深度学习（Deep Learning）是机器学习的子领域。而线性代数（linearalgebra）是有关连续值的数学。许多计算机科学家在此方面经验不足（传统上计算机科学更偏重离散数学）。想要理解和使用许多机器学习算法，特别是深度学习算法，对线性代数的良好理解是不可或缺的。

为什么要学数学？

线性代数、概率论和微积分是确切地表达机器学习的“语言”。学习这些主题有助于形成对机器学习算法底层机制的深入理解，也有助于开发新的算法。

如果我们查看的尺度足够小，那么深度学习背后的一切都是数学。所以在开始深度学习之前，有必要理解基本的线性代数。

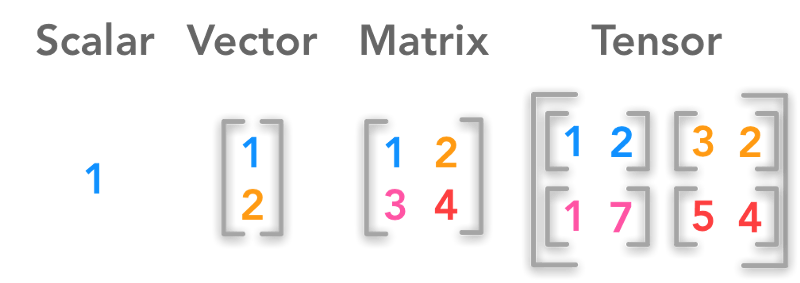
标量、向量、矩阵、张量；图片来源：hadrienj.github.io

深度学习背后的核心数据结构是标量（Scalar）、向量（Vector）、矩阵（Matrix）、张量（Tensor）。让我们通过编程，使用这些数据结构求解基本的线性代数问题。

标量

标量是单个数字，或者说，0阶（0th-order）张量。x ∈ ℝ表示x是一个属于实数集ℝ的标量。

在深度学习中，有不同的数字集合。ℕ表示正整数集（1,2,3,…）。ℤ表示整数集，包括正数、负数和零。ℚ表示有理数集（可以表达为两个整数之比的数）。

在Python中有几个内置的标量类型：int、float、complex、bytes、Unicode。Numpy又增加了二十多个新的标量类型。

import numpy as np

np.ScalarType

返回：

(int,

float,

complex,

int,

bool,

bytes,

str,

memoryview,

numpy.bool_,

numpy.int8,

numpy.uint8,

numpy.int16,

numpy.uint16,

numpy.int32,

numpy.uint32,

numpy.int64,

numpy.uint64,

numpy.int64,

numpy.uint64,

numpy.float16,

numpy.float32,

numpy.float64,

numpy.float128,

numpy.complex64,

numpy.complex128,

numpy.complex256,

numpy.object_,

numpy.bytes_,

numpy.str_,

numpy.void,

numpy.datetime64,

numpy.timedelta64)

其中，以下划线（_）结尾的数据类型和对应的Python内置类型基本上是等价的。

在Python中定义标量和一些运算

下面的代码演示了一些张量的算术运算。

a = 5

b = 7.5

print(type(a))

print(type(b))

print(a + b)

print(a - b)

print(a * b)

print(a / b)

输出：

12.5

-2.5

37.5

0.6666666666666666

下面的代码段检查给定的变量是否是标量：

import numpy as np

def isscalar(num):

if isinstance(num, generic):

returnTrue

else:

returnFalse

print(np.isscalar(3.1))

print(np.isscalar([3.1]))

print(np.isscalar(False))

输出：

True

False

True

向量

向量是由单个数字组成的有序数组，或者说，1阶张量。向量是向量空间这一对象的组成部分。向量空间是特定长度（又叫维度）的所有可能的向量的整个集合。三维实数向量空间（ℝ3）常用于表示现实世界中的三维空间。

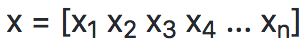
为了指明向量的分量（component），向量的第i个标量元素记为x[i]。

在深度学习中，向量通常用来表示特征向量。

在Python中定义向量和一些运算

声明向量：

x = [1, 2, 3]

y = [4, 5, 6]

print(type(x))

输出：

+并不表示向量的加法，而是列表的连接：

print(x + y)

输出：

[1, 2, 3, 4, 5, 6]

需要使用Numpy进行向量加法：

z = np.add(x, y)

print(z)

print(type(z))

输出：

[579]

向量的叉积（cross product）

两个向量的叉积向量，大小等于以这两个向量为邻边的平行四边形面积，方向与这两个向量所在平面垂直：

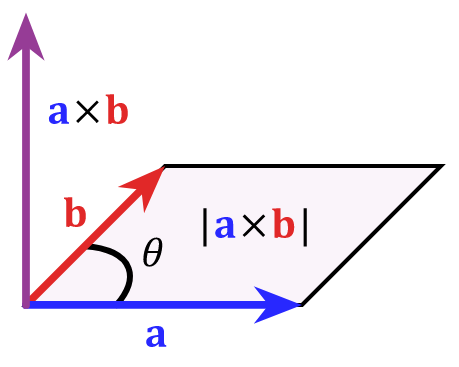
图片来源：维基百科

np.cross(x, y)

返回：

[-36 -3]

向量的点积（dot product）

向量的点积为标量，对于给定长度但方向不同的两个向量而言，方向差异越大，点积越小。

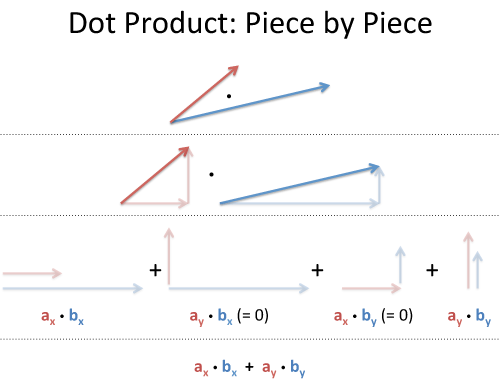
图片来源：betterexplained.com

np.dot(x, y)

返回：

32

矩阵

矩阵是由数字组成的矩形数组，或者说，2阶张量。如果m和n为正整数，即，m, n ∈ ℕ，那么，一个m x n矩阵包含m * n个数字，m行n列。

m x n可表示为以下形式：

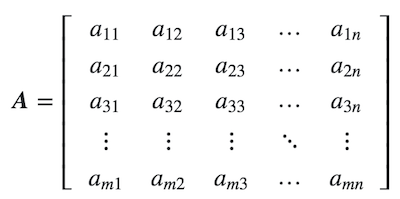
有时简写为：

在Python中定义矩阵和一些运算

在Python中，我们使用numpy库创建n维数组，也就是矩阵。我们将列表传入matrix方法，以定义矩阵。

x = np.matrix([[1,2],[3,4]])

x

返回：

matrix([[1, 2],

[3, 4]])

矩阵第0轴的元素均值：

x.mean(0)

返回：

matrix([[2., 3.]]) # (1+3)/2, (3+4)/2

矩阵第1轴的元素均值：

x.mean(1)

返回：

z = x.mean(1)

z

返回：

matrix([[1.5], # (1+2)/2

[3.5]]) # (3+4)/2

shape属性返回矩阵的形状：

z.shape

返回：

(2, 1)

所以，矩阵z有2行1列。

顺便提下，向量的shape属性返回由单个数字（向量的长度）组成的元组：

np.shape([1, 2, 3])

返回：

(3,)

而标量的shape属性返回一个空元祖：

np.shape(1)

返回：

()

矩阵加法和乘法

矩阵可以和标量及其他矩阵相加、相乘。这些运算在数学上都有精确的定义。机器学习和深度学习经常使用这些运算，所以有必要熟悉这些运算。

对矩阵求和：

x = np.matrix([[1, 2], [4, 3]])

x.sum()

返回：

10

矩阵-标量加法

在矩阵的每个元素上加上给定标量：

x = np.matrix([[1, 2], [4, 3]])

x + 1

返回：

matrix([[2, 3],

[5, 4]])

矩阵-标量乘法

类似地，矩阵-标量乘法就是在矩阵的每个元素上乘以给定标量：

x * 3

返回：

matrix([[ 3, 6],

[12, 9]])

矩阵-矩阵加法

形状相同的矩阵才能相加。两个矩阵对应位置的元素之和作为新矩阵的元素，而新矩阵的形状和原本两个矩阵一样。

x = np.matrix([[1, 2], [4, 3]])

y = np.matrix([[3, 4], [3, 10]])

x和y的形状均为(2, 2)。

x + y

返回：

matrix([[ 4, 6],

[ 7, 13]])

矩阵-矩阵乘法

形状为m x n的矩阵与形状为n x p的矩阵相乘，得到形状为m x p的矩阵。

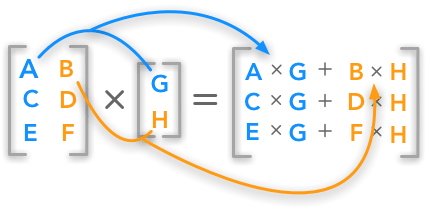
图片来源：hadrienj.github.io

从编程的角度，矩阵乘法的一个直观解释是，一个矩阵是数据，另一个矩阵是即将应用于数据的函数（操作）：

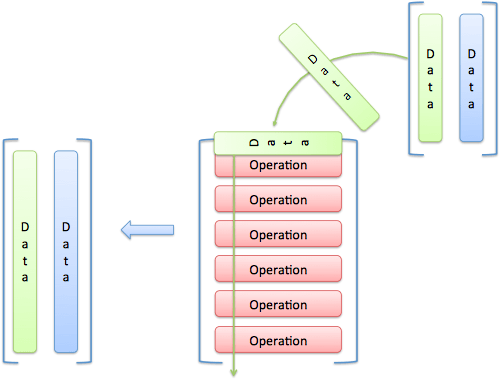
图片来源：betterexplained.com

x = np.matrix([[1, 2], [3, 4], [5, 6]])

y = np.matrix([[7], [13]]

x * y

返回：

matrix([[ 33],

[ 73],

[113]])

上面的代码中，矩阵x的形状为(3, 2)，矩阵y的形状为(2, 1)，故所得矩阵的形状为(3, 1)。如果x的列数不等于y的行数，则x和y不能相乘，强行相乘会报错shapes not aligned。

矩阵转置

矩阵转置交换原矩阵的行和列（行变为列，列变为行），即：

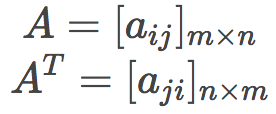
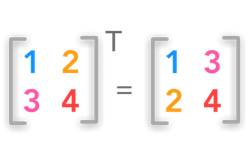
x = np.matrix([[1, 2], [3, 4], [5, 6]])

x

返回：

matrix([[1, 2],

[3, 4],

[5, 6]])

使用numpy提供的transpose()方法转置矩阵：

x.transpose()

返回：

matrix([[1, 3, 5],

[2, 4, 6]])

张量

比标量、向量、矩阵更通用的是张量概念。在物理科学和机器学习中，有时有必要使用超过二阶的张量（还记得吗？标量、向量、矩阵分别可以视为0、1、2阶张量。）

图片来源：refactored.ai

在Python中定义张量和一些运算

张量当然也可以用numpy表示（超过二阶的张量不过是超过二维的数组）：

import numpy as np

t = np.array([

[[1,2,3], [4,5,6], [7,8,9]],

[[11,12,13], [14,15,16], [17,18,19]],

[[21,22,23], [24,25,26], [27,28,29]],

])

t.shape

返回：

(3, 3, 3)

张量加法

s = np.array([

[[1,2,3], [4,5,6], [7,8,9]],

[[10, 11, 12], [13, 14, 15], [16, 17, 18]],

[[19, 20, 21], [22, 23, 24], [25, 26, 27]],

])

s + t

返回：

array([[[ 2, 4, 6],

[ 8, 10, 12],

[14, 16, 18]],

[[21, 23, 25],

[27, 29, 31],

[33, 35, 37]],

[[40, 42, 44],

[46, 48, 50],

[52, 54, 56]]])

张量乘法

s * t得到的是阿达马乘积（Hadamard Product），也就是分素相乘（element-wise multiplication），将张量s和t中的每个元素相乘，所得乘积为结果张量对应位置的元素。

s * t

返回：

array([[[ 1, 4, 9],

[ 16, 25, 36],

[ 49, 64, 81]],

[[110, 132, 156],

[182, 210, 240],

[272, 306, 342]],

[[399, 440, 483],

[528, 575, 624],

[675, 728, 783]]])

张量积（Tensor Product）需要使用numpy的tensordot方法计算。

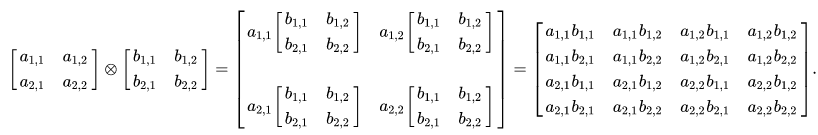
图片来源：维基百科

计算s ⊗ t：

s = np.array([[[1, 2], [3, 4]]])

t = np.array([[[5, 6], [7, 8]]])

np.tensordot(s, t, 0)

返回：

array([[[[[[ 5, 6],

[ 7, 8]]],

[[[10, 12],

[14, 16]]]],

[[[[15, 18],

[21, 24]]],

[[[20, 24],

[28, 32]]]]]])

其中，最后一个参数0表示求张量积。当该参数为1时，表示求张量的点积（tensor dot product），这一运算可以视为向量点积概念的推广；当该参数为2时，表示求张量的缩并（tensor double contraction），这一运算可以视为矩阵乘法概念的推广。

当然，由于张量常用于深度学习，因此我们也经常直接使用深度学习框架表达张量。比如，在PyTorch中，创建一个形状为(5, 5)的张量，然后用浮点数1填充该张量：

torch.ones(5, 5)

返回：

tensor([[ 1., 1., 1., 1., 1.],

[ 1., 1., 1., 1., 1.],

[ 1., 1., 1., 1., 1.],

[ 1., 1., 1., 1., 1.],

[ 1., 1., 1., 1., 1.]])