▌一. 前言:
作为AI入门小白,参考了一些文章,想记点笔记加深印象,发出来是给有需求的童鞋学习共勉,大神轻拍!
【毒鸡汤】:算法这东西,读完之后的状态多半是 -->“我是谁,我在哪?”没事的,吭哧吭哧学总能学会,毕竟还有千千万万个算法等着你。
本文货很干,堪比沙哈拉大沙漠,自己挑的文章,含着泪也要读完!
▌二. 科普:
生物上的神经元就是接收四面八方的刺激(输入),然后做出反应(输出),给它一点☀️就灿烂。
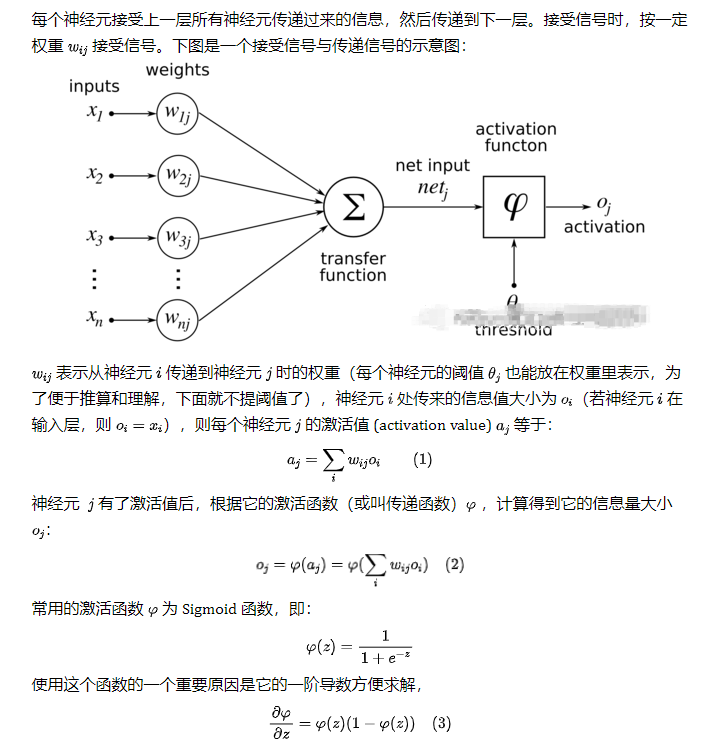
仿生嘛,于是喜欢放飞自我的某些人就提出了人工神经网络。一切的基础-->人工神经单元,看图:
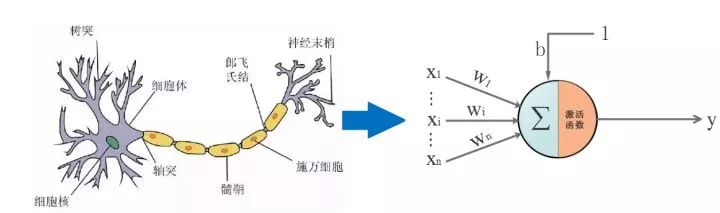
▌三. 通往沙漠的入口: 神经元是什么,有什么用:
开始前,需要搞清楚一个很重要的问题:人工神经网络里的神经元是什么,有什么用。只有弄清楚这个问题,你才知道你在哪里,在做什么,要往哪里去。
首先,回顾一下神经元的结构,看下图, 我们先忽略激活函数不管:
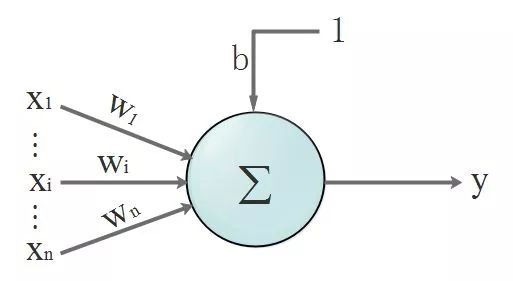

没错,开始晒公式了!我们的数据都是离散的,为了看得更清楚点,所以换个表达方式,把离散的数据写成向量。该不会忘了向量是啥吧?回头致电问候一下当年的体育老师!

现在回答问题刚才的问题:
一个神经元是什么:参照式(1.6),从函数图像角度看,这就是一根直线。
一个神经元有什么用:要说明用途就要给出一个应用场景:分类。一个神经元就是一条直线,相当于楚河汉界,可以把红棋绿棋分隔开,此时它就是个分类器。所以,在线性场景下,单个神经元能达到分类的作用,它总能学习到一条合适的直线,将两类元素区分出来。
先睹为快,看效果图,自己可以去玩:传送门
http://t.cn/RBCoWof
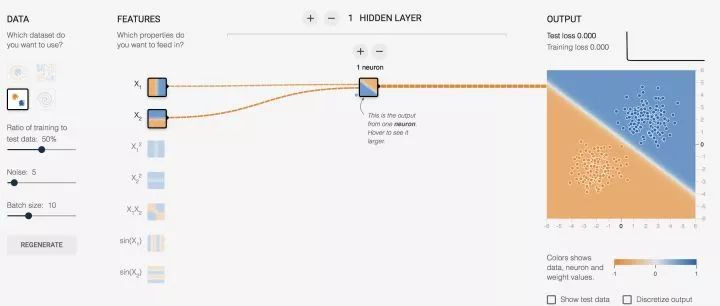
对上面的图简单说明一下:
(x1,x2) 对于神经元的输入都是 x, 而对我们而言,这数据就是意义上的点的坐标,我们习惯写成 (x,y)。
又要划重点了:
我们需要对神经元的输出做判定,那么就需要有判定规则,通过判定规则后我们才能拿到我们想要的结果,这个规则就是:
假设,0代表红点,1代表蓝点(这些数据都是事先标定好的,在监督学习下,神经元会知道点是什么颜色并以这个已知结果作为标杆进行学习)
当神经元输出小于等于 0 时,最终结果输出为 0,这是个红点
当神经元输出大于 1 时,最终结果输出为 1,这是个蓝点
上面提到的规则让我闻到了激活函数的味道!(这里只是线性场景,虽然不合适,但是简单起见,使用了单位阶跃函数来描述激活函数的功能)当 x<=0 时,y = 0; 当 x > 0 时,y = 1
这是阶跃函数的长相:
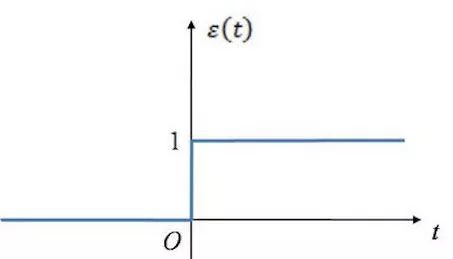
此时神经元的长相:
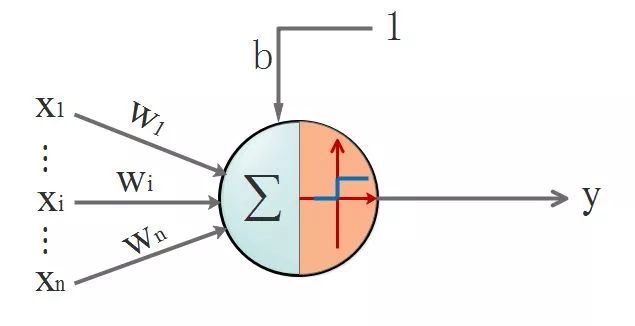
▌四. 茫茫大漠第一步: 激活函数是什么,有什么用
从上面的例子,其实已经说明了激活函数的作用;但是,我们通常面临的问题,不是简单的线性问题,不能用单位阶跃函数作为激活函数,原因是:
阶跃函数在x=0时不连续,即不可导,在非0处导数为0。用人话说就是它具备输出限定在[0-1],但是它不具备丝滑的特性,这个特性很重要。并且在非0处导数为0,也就是硬饱和,压根儿就没梯度可言,梯度也很重要,梯度意味着在神经元传播间是有反应的,而不是“死”了的。
接下来说明下,激活函数所具备的特性有什么,只挑重要的几点特性讲:
非线性:即导数不是常数,不然就退化成直线。对于一些画一条直线仍然无法分开的问题,非线性可以把直线掰弯,自从变弯以后,就能包罗万象了。
几乎处处可导:也就是具备“丝滑的特性”,不要应激过度,要做正常人。数学上,处处可导为后面降到的后向传播算法(BP算法)提供了核心条件
输出范围有限:一般是限定在[0,1],有限的输出范围使得神经元对于一些比较大的输入也会比较稳定。
非饱和性:饱和就是指,当输入比较大的时候,输出几乎没变化了,那么会导致梯度消失!什么是梯度消失:就是你天天给女生送花,一开始妹纸还惊喜,到后来直接麻木没反应了。梯度消失带来的负面影响就是会限制了神经网络表达能力,词穷的感觉你有过么。sigmod,tanh函数都是软饱和的,阶跃函数是硬饱和。软是指输入趋于无穷大的时候输出无限接近上线,硬是指像阶跃函数那样,输入非0输出就已经始终都是上限值。数学表示我就懒得写了,传送门在此(https://www.cnblogs.com/rgvb178/p/6055213.html),里面有写到。如果激活函数是饱和的,带来的缺陷就是系统迭代更新变慢,系统收敛就慢,当然这是可以有办法弥补的,一种方法是使用交叉熵函数作为损失函数,这里不多说。ReLU是非饱和的,亲测效果挺不错,所以这货最近挺火的。
单调性:即导数符号不变。导出要么一直大于0,要么一直小于0,不要上蹿下跳。导数符号不变,让神经网络训练容易收敛。
这里只说我们用到的激活函数:
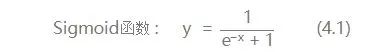
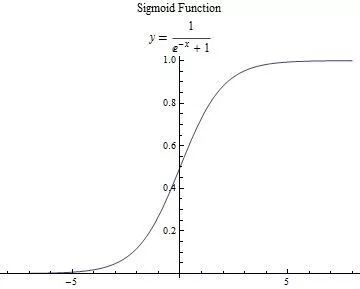
求一下它的导数把,因为后面讲bp算法会直接套用它:
先祭出大杀器,高中数学之复合函数求导法则:

它的导数图像:
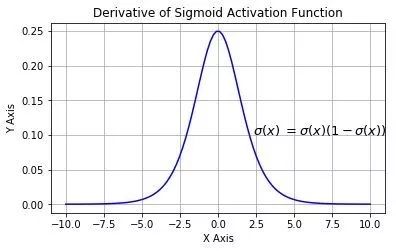
▌五. 沙漠中心的风暴:BP(Back Propagation)算法
1. 神经网络的结构
经过上面的介绍,单个神经元不足以让人心动,唯有组成网络。神经网络是一种分层结构,一般由输入曾,隐藏层,输出层组成。所以神经网络至少有3层,隐藏层多于1,总层数大于3的就是我们所说的深度学习了。
输入层:就是接收原始数据,然后往隐层送
输出层:神经网络的决策输出
隐藏层:该层可以说是神经网络的关键,相当于对数据做一次特征提取。隐藏层的意义,是把前一层的向量变成新的向量。就是坐标变换,说人话就是把数据做平移,旋转,伸缩,扭曲,让数据变得线性可分。可能这个不那么好理解,举个栗子:
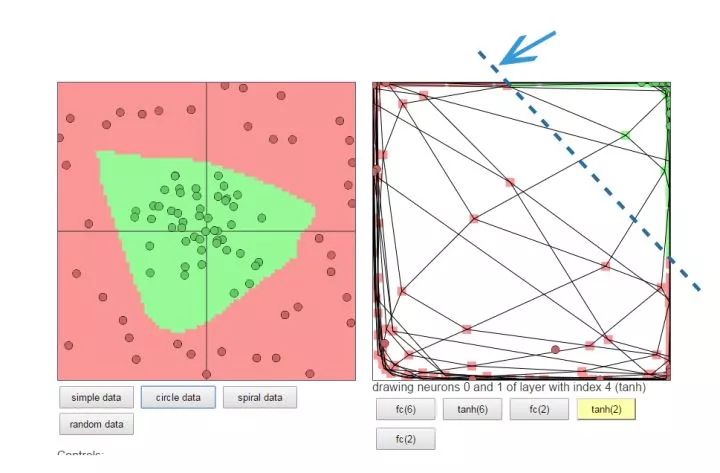
下面的图左侧是原始数据,中间很多绿点,外围是很多红点,如果你是神经网络,你会怎么做呢?
一种做法:把左图的平面看成一块布,把它缝合成一个闭合的包包(相当于数据变换到了一个3维坐标空间),然后把有绿色点的部分撸到顶部(伸缩和扭曲),然后外围的红色点自然在另一端了,要是姿势还不够帅,就挪挪位置(平移)。这时候干脆利落的砍一刀,绿点红点就彻底区分开了。
重要的东西再说一遍:神经网络换着坐标空间玩数据,根据需要,可降维,可升维,可大,可小,可圆可扁,就是这么“无敌”
这个也可以自己去玩玩,直观的感受一下:传送门
2.正反向传播过程
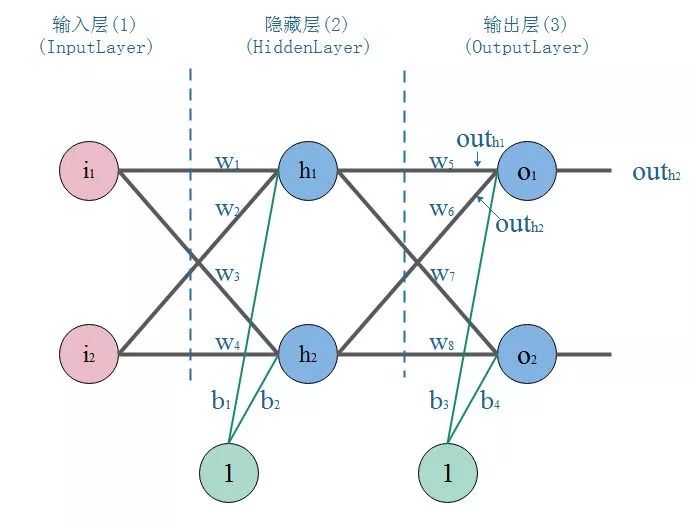
看图,这是一个典型的三层神经网络结构,第一层是输入层,第二层是隐藏层,第三层是输出层。PS:不同的应用场景,神经网络的结构要有针对性的设计,这里仅仅是为了推导算法和计算方便才采用这个简单的结构
我们以战士打靶,目标是训练战士能命中靶心成为神枪手作为场景:
那么我们手里有这样一些数据:一堆枪摆放的位置(x,y),以及射击结果,命中靶心和不命中靶心。
我们的目标是:训练出一个神经网络模型,输入一个点的坐标(射击姿势),它就告诉你这个点是什么结果(是否命中)。
我们的方法是:训练一个能根据误差不断自我调整的模型,训练模型的步骤是:
正向传播:把点的坐标数据输入神经网络,然后开始一层一层的传播下去,直到输出层输出结果。
反向传播(BP):就好比战士去靶场打靶,枪的摆放位置(输入),和靶心(期望的输出)是已知。战士(神经网络)一开始的时候是这样做的,随便开一枪(w,b参数初始化称随机值),观察结果(这时候相当于进行了一次正向传播)。然后发现,偏离靶心左边,应该往右点儿打。所以战士开始根据偏离靶心的距离(误差,也称损失)调整了射击方向往右一点(这时,完成了一次反向传播)
当完成了一次正反向传播,也就完成了一次神经网络的训练迭代,反复调整射击角度(反复迭代),误差越来越小,战士打得越来越准,神枪手模型也就诞生了。
3.BP算法推导和计算
参数初始化:

正向传播:

2.隐层-->输出层:

正向传播结束,我们看看输出层的输出结果:[0.7987314002, 0.8374488853],但是我们希望它能输出[0.01, 0.99],所以明显的差太远了,这个时候我们就需要利用反向传播,更新权值w,然后重新计算输出.
反向传播:
1.计算输出误差:

PS: 这里我要说的是,用这个作为误差的计算,因为它简单,实际上用的时候效果不咋滴。如果激活函数是饱和的,带来的缺陷就是系统迭代更新变慢,系统收敛就慢,当然这是可以有办法弥补的,一种方法是使用交叉熵函数作为损失函数。
交叉熵做为代价函数能达到上面说的优化系统收敛下欧工,是因为它在计算误差对输入的梯度时,抵消掉了激活函数的导数项,从而避免了因为激活函数的“饱和性”给系统带来的负面影响。如果项了解更详细的证明可以点 -->传送门(https://blog.csdn.net/lanchunhui/article/details/50086025)
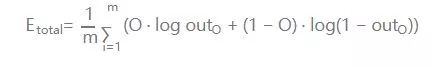
对输出的偏导数:
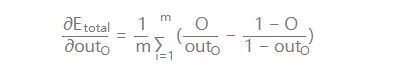
2.隐层-->输出层的权值及偏置b的更新:
先放出链式求导法则:

以更新w5举例:
我们知道,权重w的大小能直接影响输出,w不合适那么会使得输出误差。要想直到某一个w值对误差影响的程度,可以用误差对该w的变化率来表达。如果w的一点点变动,就会导致误差增大很多,说明这个w对误差影响的程度就更大,也就是说,误差对该w的变化率越高。而误差对w的变化率就是误差对w的偏导。
所以,看下图,总误差的大小首先受输出层神经元O1的输出影响,继续反推,O1的输出受它自己的输入的影响,而它自己的输入会受到w5的影响。这就是连锁反应,从结果找根因。
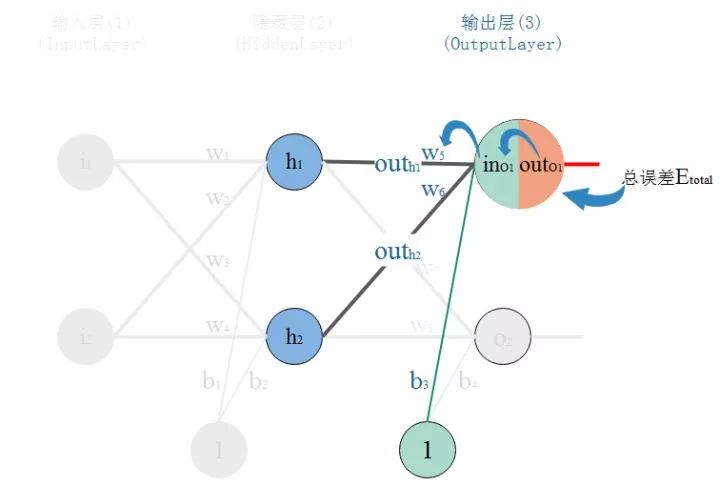
那么,根据链式法则则有:
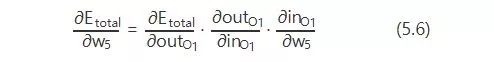
现在挨个计算:


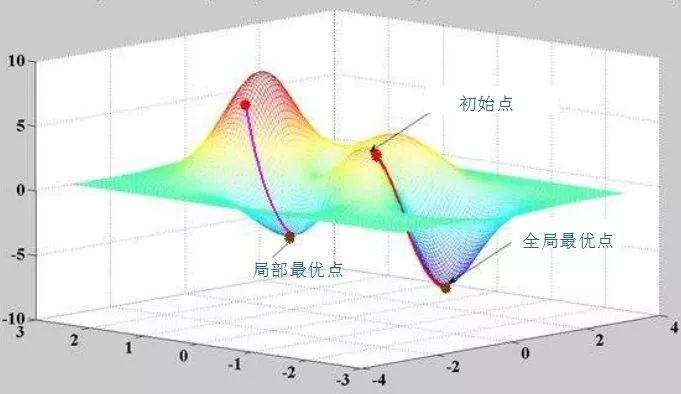
有个学习率的东西,学习率取个0.5。关于学习率,不能过高也不能过低。因为训练神经网络系统的过程,就是通过不断的迭代,找到让系统输出误差最小的参数的过程。每一次迭代都经过反向传播进行梯度下降,然而误差空间不是一个滑梯,一降到底,常规情况下就像坑洼的山地。学习率太小,那就很容易陷入局部最优,就是你认为的最低点并不是整个空间的最低点。如果学习率太高,那系统可能难以收敛,会在一个地方上串下跳,无法对准目标(目标是指误差空间的最低点),可以看图:
xy轴是权值w平面,z轴是输出总误差。整个误差曲面可以看到两个明显的低点,显然右边最低,属于全局最优。而左边的是次低,从局部范围看,属于局部最优。而图中,在给定初始点的情况下,标出的两条抵达低点的路线,已经是很理想情况的梯度下降路径。

3.输入层-->隐层的权值及偏置b更新:
以更新w1为例:仔细观察,我们在求w5的更新,误差反向传递路径输出层-->隐层,即out(O1)-->in(O1)-->w5,总误差只有一根线能传回来。但是求w1时,误差反向传递路径是隐藏层-->输入层,但是隐藏层的神经元是有2根线的,所以总误差沿着2个路径回来,也就是说,计算偏导时,要分开来算。看图:
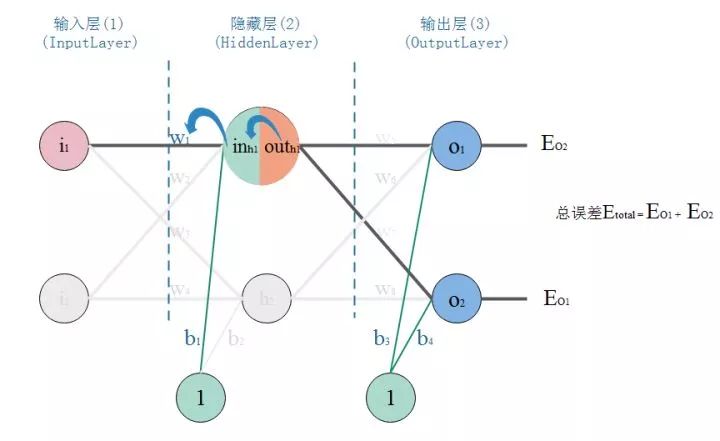
那么,现在开始算总误差对w1的偏导:





4.结论:
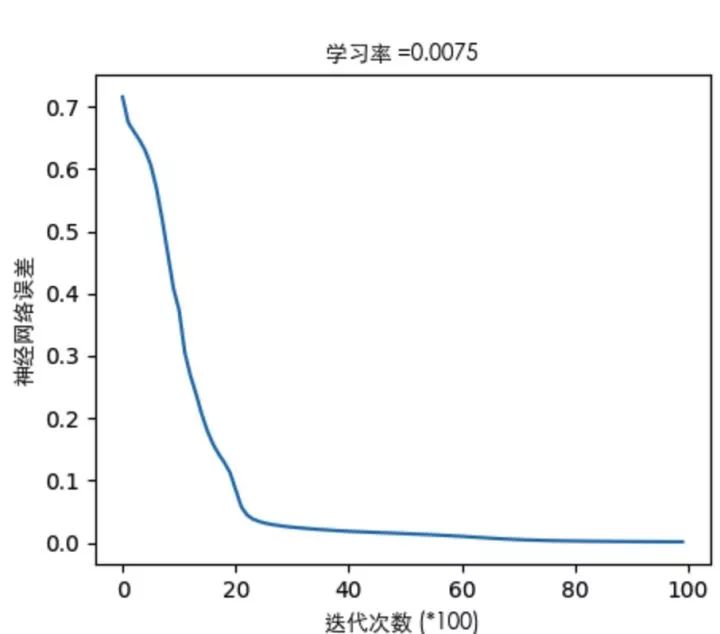
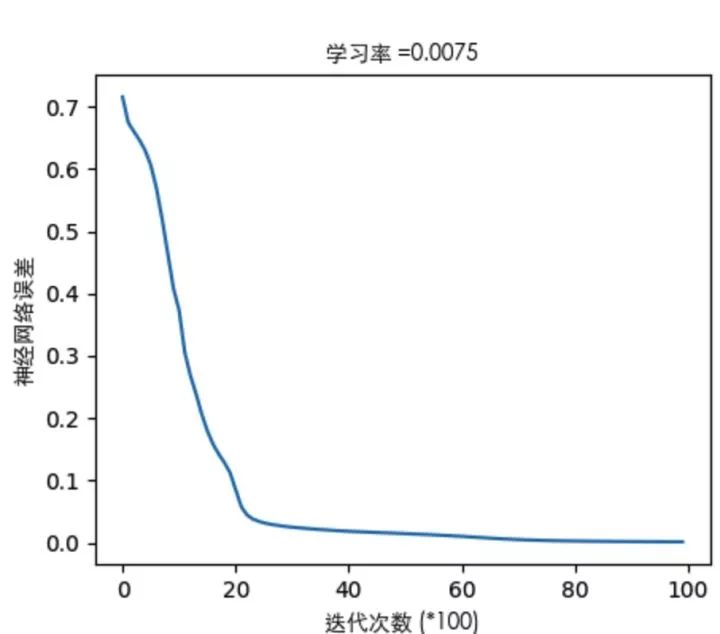
我们通过亲力亲为的计算,走过了正向传播,也体会了反向传播,完成了一次训练(迭代)。随着迭代加深,输出层的误差会越来越小,专业点说就是系统趋于收敛。来一张系统误差随迭代次数变化的图来表明我刚才说描述:
▌六. 沙漠的绿洲:代码实现
1. 代码代码!
其实已经有很多机器学习的框架可以很简单的实现神经网络。但是我们的目标是:在看懂算法之后,我们是否能照着算法的整个过程,去实现一遍,可以加深对算法原理的理解,以及对算法实现思路的的理解。顺便说打个call,numpy这个库,你值得拥有!
代码实现如下。代码里已经做了尽量啰嗦的注释,关键实现的地方对标了公式的编号,如果看的不明白的地方多回来啃一下算法推导。对应代码也传到了github上。
代码能自己定义神经网络的结构,支持深度网络。代码实现了对红蓝颜色的点做分类的模型训练,通过3层网络结构,改变隐藏层的神经元个数,通过图形显示隐藏层神经元数量对问题的解释能力。
代码中还实现了不同激活函数。隐藏层可以根据需要换着激活函数玩,输出层一般就用sigmoid,当然想换也随你喜欢~
#coding:utf-8importh5pyimportsklearn.datasetsimportsklearn.linear_modelimportmatplotlibimportmatplotlib.font_managerasfmimportmatplotlib.pyplotaspltimportnumpyasnpnp.random.seed(1)font=fm.FontProperties(fname='/System/Library/Fonts/STHeitiLight.ttc')matplotlib.rcParams['figure.figsize']=(10.0,8.0)defsigmoid(input_sum):"""函数:激活函数Sigmoid输入:input_sum:输入,即神经元的加权和返回:output:激活后的输出input_sum:把输入缓存起来返回"""output=1.0/(1+np.exp(-input_sum))returnoutput,input_sumdefsigmoid_back_propagation(derror_wrt_output,input_sum):"""函数:误差关于神经元输入的偏导:dE/dIn=dE/dOut*dOut/dIn参照式(5.6)其中:dOut/dIn就是激活函数的导数dy=y(1-y),见式(5.9)dE/dOut误差对神经元输出的偏导,见式(5.8)输入:derror_wrt_output:误差关于神经元输出的偏导:dE/dyⱼ=1/2(d(expect_to_output-output)**2/doutput)=-(expect_to_output-output)input_sum:输入加权和返回:derror_wrt_dinputs:误差关于输入的偏导,见式(5.13)"""output=1.0/(1+np.exp(-input_sum))doutput_wrt_dinput=output*(1-output)derror_wrt_dinput=derror_wrt_output*doutput_wrt_dinputreturnderror_wrt_dinputdefrelu(input_sum):"""函数:激活函数ReLU输入:input_sum:输入,即神经元的加权和返回:outputs:激活后的输出input_sum:把输入缓存起来返回"""output=np.maximum(0,input_sum)returnoutput,input_sumdefrelu_back_propagation(derror_wrt_output,input_sum):"""函数:误差关于神经元输入的偏导:dE/dIn=dE/dOut*dOut/dIn其中:dOut/dIn就是激活函数的导数dE/dOut误差对神经元输出的偏导输入:derror_wrt_output:误差关于神经元输出的偏导input_sum:输入加权和返回:derror_wrt_dinputs:误差关于输入的偏导"""derror_wrt_dinputs=np.array(derror_wrt_output,copy=True)derror_wrt_dinputs[input_sum<= 0] = 0 return derror_wrt_dinputsdef tanh(input_sum): """ 函数: 激活函数 tanh 输入: input_sum: 输入,即神经元的加权和 返回: output: 激活后的输出 input_sum: 把输入缓存起来返回 """ output = np.tanh(input_sum) return output, input_sumdef tanh_back_propagation(derror_wrt_output, input_sum): """ 函数: 误差关于神经元输入的偏导: dE/dIn = dE/dOut * dOut/dIn 其中: dOut/dIn 就是激活函数的导数 tanh'(x) = 1 - x² dE/dOut 误差对神经元输出的偏导 输入: derror_wrt_output:误差关于神经元输出的偏导: dE/dyⱼ = 1/2(d(expect_to_output - output)**2/doutput) = -(expect_to_output - output) input_sum: 输入加权和 返回: derror_wrt_dinputs: 误差关于输入的偏导 """ output = np.tanh(input_sum) doutput_wrt_dinput = 1 - np.power(output, 2) derror_wrt_dinput = derror_wrt_output * doutput_wrt_dinput return derror_wrt_dinputdef activated(activation_choose, input): """把正向激活包装一下""" if activation_choose == "sigmoid": return sigmoid(input) elif activation_choose == "relu": return relu(input) elif activation_choose == "tanh": return tanh(input) return sigmoid(input)def activated_back_propagation(activation_choose, derror_wrt_output, output): """包装反向激活传播""" if activation_choose == "sigmoid": return sigmoid_back_propagation(derror_wrt_output, output) elif activation_choose == "relu": return relu_back_propagation(derror_wrt_output, output) elif activation_choose == "tanh": return tanh_back_propagation(derror_wrt_output, output) return sigmoid_back_propagation(derror_wrt_output, output)class NeuralNetwork: def __init__(self, layers_strcuture, print_cost = False): self.layers_strcuture = layers_strcuture self.layers_num = len(layers_strcuture) # 除掉输入层的网络层数,因为其他层才是真正的神经元层 self.param_layers_num = self.layers_num - 1 self.learning_rate = 0.0618 self.num_iterations = 2000 self.x = None self.y = None self.w = dict() self.b = dict() self.costs = [] self.print_cost = print_cost self.init_w_and_b() def set_learning_rate(self, learning_rate): """设置学习率""" self.learning_rate = learning_rate def set_num_iterations(self, num_iterations): """设置迭代次数""" self.num_iterations = num_iterations def set_xy(self, input, expected_output): """设置神经网络的输入和期望的输出""" self.x = input self.y = expected_output def init_w_and_b(self): """ 函数: 初始化神经网络所有参数 输入: layers_strcuture: 神经网络的结构,例如[2,4,3,1],4层结构: 第0层输入层接收2个数据,第1层隐藏层4个神经元,第2层隐藏层3个神经元,第3层输出层1个神经元 返回: 神经网络各层参数的索引表,用来定位权值 wᵢ 和偏置 bᵢ,i为网络层编号 """ np.random.seed(3) # 当前神经元层的权值为 n_i x n_(i-1)的矩阵,i为网络层编号,n为下标i代表的网络层的节点个数 # 例如[2,4,3,1],4层结构:第0层输入层为2,那么第1层隐藏层神经元个数为4 # 那么第1层的权值w是一个 4x2 的矩阵,如: # w1 = array([ [-0.96927756, -0.59273074], # [ 0.58227367, 0.45993021], # [-0.02270222, 0.13577601], # [-0.07912066, -1.49802751] ]) # 当前层的偏置一般给0就行,偏置是个1xnᵢ的矩阵,nᵢ为第i层的节点个数,例如第1层为4个节点,那么: # b1 = array([ 0., 0., 0., 0.]) for l in range(1, self.layers_num): self.w["w" + str(l)] = np.random.randn(self.layers_strcuture[l], self.layers_strcuture[l-1])/np.sqrt(self.layers_strcuture[l-1]) self.b["b" + str(l)] = np.zeros((self.layers_strcuture[l], 1)) return self.w, self.b def layer_activation_forward(self, x, w, b, activation_choose): """ 函数: 网络层的正向传播 输入: x: 当前网络层输入(即上一层的输出),一般是所有训练数据,即输入矩阵 w: 当前网络层的权值矩阵 b: 当前网络层的偏置矩阵 activation_choose: 选择激活函数 "sigmoid", "relu", "tanh" 返回: output: 网络层的激活输出 cache: 缓存该网络层的信息,供后续使用: (x, w, b, input_sum) ->cache"""#对输入求加权和,见式(5.1)input_sum=np.dot(w,x)+b#对输入加权和进行激活输出output,_=activated(activation_choose,input_sum)returnoutput,(x,w,b,input_sum)defforward_propagation(self,x):"""函数:神经网络的正向传播输入:返回:output:正向传播完成后的输出层的输出caches:正向传播过程中缓存每一个网络层的信息:(x,w,b,input_sum),...->caches"""caches=[]#作为输入层,输出=输入output_prev=x#第0层为输入层,只负责观察到输入的数据,并不需要处理,正向传播从第1层开始,一直到输出层输出为止#range(1,n)=>[1,2,...,n-1]L=self.param_layers_numforlinrange(1,L):#当前网络层的输入来自前一层的输出input_cur=output_prevoutput_prev,cache=self.layer_activation_forward(input_cur,self.w["w"+str(l)],self.b["b"+str(l)],"tanh")caches.append(cache)output,cache=self.layer_activation_forward(output_prev,self.w["w"+str(L)],self.b["b"+str(L)],"sigmoid")caches.append(cache)returnoutput,cachesdefshow_caches(self,caches):"""显示网络层的缓存参数信息"""i=1forcacheincaches:print("%dtdLayer"%i)print("input:%s"%cache[0])print("w:%s"%cache[1])print("b:%s"%cache[2])print("input_sum:%s"%cache[3])print("----------")i+=1defcompute_error(self,output):"""函数:计算档次迭代的输出总误差输入:返回:"""m=self.y.shape[1]#计算误差,见式(5.5):E=Σ1/2(期望输出-实际输出)²#error=np.sum(0.5*(self.y-output)**2)/m#交叉熵作为误差函数error=-np.sum(np.multiply(np.log(output),self.y)+np.multiply(np.log(1-output),1-self.y))/merror=np.squeeze(error)returnerrordeflayer_activation_backward(self,derror_wrt_output,cache,activation_choose):"""函数:网络层的反向传播输入:derror_wrt_output:误差关于输出的偏导cache:网络层的缓存信息(x,w,b,input_sum)activation_choose:选择激活函数"sigmoid","relu","tanh"返回:梯度信息,即derror_wrt_output_prev:反向传播到上一层的误差关于输出的梯度derror_wrt_dw:误差关于权值的梯度derror_wrt_db:误差关于偏置的梯度"""input,w,b,input_sum=cacheoutput_prev=input#上一层的输出=当前层的输入;注意是'输入'不是输入的加权和(input_sum)m=output_prev.shape[1]#m是输入的样本数量,我们要取均值,所以下面的求值要除以m#实现式(5.13)->误差关于权值w的偏导数derror_wrt_dinput=activated_back_propagation(activation_choose,derror_wrt_output,input_sum)derror_wrt_dw=np.dot(derror_wrt_dinput,output_prev.T)/m#实现式(5.32)->误差关于偏置b的偏导数derror_wrt_db=np.sum(derror_wrt_dinput,axis=1,keepdims=True)/m#为反向传播到上一层提供误差传递,见式(5.28)的(Σδ·w)部分derror_wrt_output_prev=np.dot(w.T,derror_wrt_dinput)returnderror_wrt_output_prev,derror_wrt_dw,derror_wrt_dbdefback_propagation(self,output,caches):"""函数:神经网络的反向传播输入:output:神经网络输caches:所有网络层(输入层不算)的缓存参数信息[(x,w,b,input_sum),...]返回:grads:返回当前迭代的梯度信息"""grads={}L=self.param_layers_num#output=output.reshape(output.shape)#把输出层输出输出重构成和期望输出一样的结构expected_output=self.y#见式(5.8)#derror_wrt_output=-(expected_output-output)#交叉熵作为误差函数derror_wrt_output=-(np.divide(expected_output,output)-np.divide(1-expected_output,1-output))#反向传播:输出层->隐藏层,得到梯度:见式(5.8),(5.13),(5.15)current_cache=caches[L-1]#取最后一层,即输出层的参数信息grads["derror_wrt_output"+str(L)],grads["derror_wrt_dw"+str(L)],grads["derror_wrt_db"+str(L)]=self.layer_activation_backward(derror_wrt_output,current_cache,"sigmoid")#反向传播:隐藏层->隐藏层,得到梯度:见式(5.28)的(Σδ·w),(5.28),(5.32)forlinreversed(range(L-1)):current_cache=caches[l]derror_wrt_output_prev_temp,derror_wrt_dw_temp,derror_wrt_db_temp=self.layer_activation_backward(grads["derror_wrt_output"+str(l+2)],current_cache,"tanh")grads["derror_wrt_output"+str(l+1)]=derror_wrt_output_prev_tempgrads["derror_wrt_dw"+str(l+1)]=derror_wrt_dw_tempgrads["derror_wrt_db"+str(l+1)]=derror_wrt_db_tempreturngradsdefupdate_w_and_b(self,grads):"""函数:根据梯度信息更新w,b输入:grads:当前迭代的梯度信息返回:"""#权值w和偏置b的更新,见式:(5.16),(5.18)forlinrange(self.param_layers_num):self.w["w"+str(l+1)]=self.w["w"+str(l+1)]-self.learning_rate*grads["derror_wrt_dw"+str(l+1)]self.b["b"+str(l+1)]=self.b["b"+str(l+1)]-self.learning_rate*grads["derror_wrt_db"+str(l+1)]deftraining_modle(self):"""训练神经网络模型"""np.random.seed(5)foriinrange(0,self.num_iterations):#正向传播,得到网络输出,以及每一层的参数信息output,caches=self.forward_propagation(self.x)#计算网络输出误差cost=self.compute_error(output)#反向传播,得到梯度信息grads=self.back_propagation(output,caches)#根据梯度信息,更新权值w和偏置bself.update_w_and_b(grads)#当次迭代结束,打印误差信息ifself.print_costandi%1000==0:print("Costafteriteration%i:%f"%(i,cost))ifself.print_costandi%1000==0:self.costs.append(cost)#模型训练完后显示误差曲线ifFalse:plt.plot(np.squeeze(self.costs))plt.ylabel(u'神经网络误差',fontproperties=font)plt.xlabel(u'迭代次数(*100)',fontproperties=font)plt.title(u"学习率="+str(self.learning_rate),fontproperties=font)plt.show()returnself.w,self.bdefpredict_by_modle(self,x):"""使用训练好的模型(即最后求得w,b参数)来决策输入的样本的结果"""output,_=self.forward_propagation(x.T)output=output.Tresult=output/np.sum(output,axis=1,keepdims=True)returnnp.argmax(result,axis=1)defplot_decision_boundary(xy,colors,pred_func):#xy是坐标点的集合,把集合的范围算出来#加减0.5相当于扩大画布的范围,不然画出来的图坐标点会落在图的边缘,逼死强迫症患者x_min,x_max=xy[:,0].min()-0.5,xy[:,0].max()+0.5y_min,y_max=xy[:,1].min()-0.5,xy[:,1].max()+0.5#以h为分辨率,生成采样点的网格,就像一张网覆盖所有颜色点h=.01xx,yy=np.meshgrid(np.arange(x_min,x_max,h),np.arange(y_min,y_max,h))#把网格点集合作为输入到模型,也就是预测这个采样点是什么颜色的点,从而得到一个决策面Z=pred_func(np.c_[xx.ravel(),yy.ravel()])Z=Z.reshape(xx.shape)#利用等高线,把预测的结果画出来,效果上就是画出红蓝点的分界线plt.contourf(xx,yy,Z,cmap=plt.cm.Spectral)#训练用的红蓝点点也画出来plt.scatter(xy[:,0],xy[:,1],c=colors,marker='o',cmap=plt.cm.Spectral,edgecolors='black')if__name__=="__main__":plt.figure(figsize=(16,32))#用sklearn的数据样本集,产生2种颜色的坐标点,noise是噪声系数,噪声越大,2种颜色的点分布越凌乱xy,colors=sklearn.datasets.make_moons(60,noise=1.0)#因为点的颜色是1bit,我们设计一个神经网络,输出层有2个神经元。#标定输出[1,0]为红色点,输出[0,1]为蓝色点expect_output=[]forcincolors:ifc==1:expect_output.append([0,1])else:expect_output.append([1,0])expect_output=np.array(expect_output).T#设计3层网络,改变隐藏层神经元的个数,观察神经网络分类红蓝点的效果hidden_layer_neuron_num_list=[1,2,4,10,20,50]fori,hidden_layer_neuron_numinenumerate(hidden_layer_neuron_num_list):plt.subplot(5,2,i+1)plt.title(u'隐藏层神经元数量:%d'%hidden_layer_neuron_num,fontproperties=font)nn=NeuralNetwork([2,hidden_layer_neuron_num,2],True)#输出和输入层都是2个节点,所以输入和输出的数据集合都要是nx2的矩阵nn.set_xy(xy.T,expect_output)nn.set_num_iterations(30000)nn.set_learning_rate(0.1)w,b=nn.training_modle()plot_decision_boundary(xy,colors,nn.predict_by_modle)plt.show()
2. 晒图晒图!
关于误差曲线(这里只举其中一个栗子):
通过看误差曲线,可以从一定程度上判定网络的效果,模型训练是否能收敛,收敛程度如何,都可以从误差曲线对梯度下降的过程能见一二。
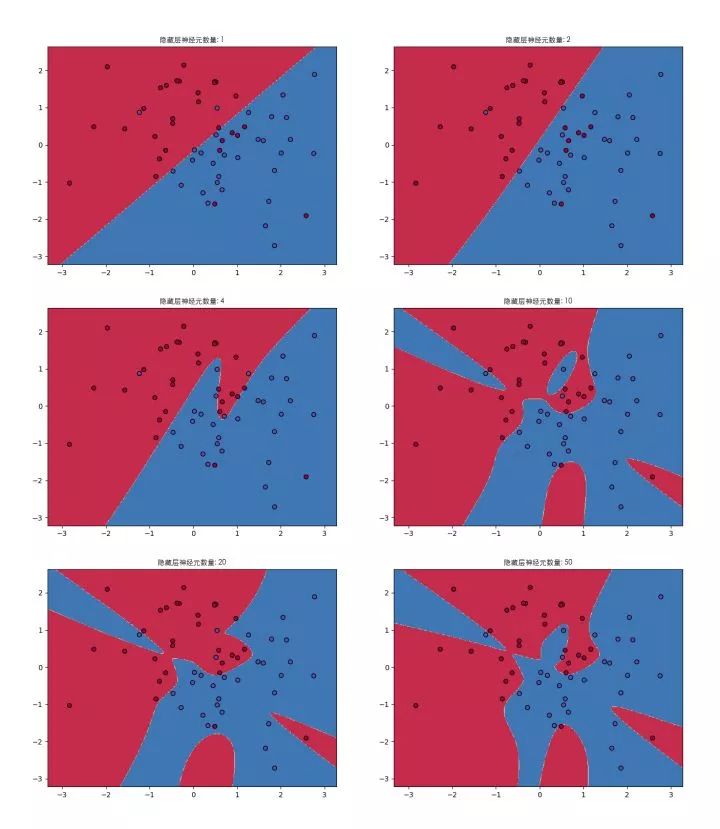
3层网络的结构下,隐藏层只有一层,看图说明一下隐藏层神经元个数变化对神经网络表达能力的影响:
当隐藏层只有1个神经元:就像文章刚开始说的,一个神经元,就是个线性分类器,表达能力就一条直线而已,见式(3.6)
2个神经元:线开始有点弯曲了,但是这次结果一点都不明显,尴尬。但从原理上神经网络开始具备了非线性表达能力
随着隐藏层神经元个数不断增加,神经网络表达能力越来越强,分类的效果越来越好。当然也不是神经元越多越好,可以开始考虑深度网络是不是效果更好一些。
▌7. 没有结局
记住一点,bp神经网络是其他各种神经网络中最简单的一种。只有学会了它,才能以此为基础展开对其他更复杂的神经网络的学习。
虽然推导了并实现了算法,但是仍然是有很多疑问,这里就作为抛砖引玉吧:
神经网络的结构,即几层网络,输入输出怎么设计才最有效?
数学理论证明,三层的神经网络就能够以任意精度逼近任何非线性连续函数。那么为什么还需要有深度网络?
在不同应用场合下,激活函数怎么选择?
学习率怎么怎么选择?
训练次数设定多少训练出的模型效果更好?
AI,从入门到放弃,首篇结束。
-
函数
+关注
关注
3文章
4327浏览量
62567 -
神经元
+关注
关注
1文章
363浏览量
18449
原文标题:AI从入门到放弃:BP神经网络算法推导及代码实现笔记
文章出处:【微信号:rgznai100,微信公众号:rgznai100】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐




 神经元和函数算法之间的关系(干货)
神经元和函数算法之间的关系(干货)











评论