基于碰撞缓解的自动驾驶控制设计
摘要 -本文介绍了一种路径规划方法，尤其是当碰撞不可避免时，通过产生尽可能减轻碰撞的轨迹。这里采用模型预测控制算法进行路径规划。为避免障碍物的产生，并减轻不可避免的碰撞，在控制目标中加入了描述障碍物和潜在碰撞严重程度的人工势场。车辆动态也被认为是最佳控制目标。基于以上分析，模型预测控制器可以保证指令的跟随、避障、车辆动态，并减轻不可避免的碰撞。仿真结果验证了所提出的MPC具有避障和减轻不可避免的碰撞的能力。
作者：Hong Wang, Yanjun Huang*, Amir Khajepour, Teng Liu, Yechen Qin,Yubiao Zhang
索引术语—碰撞缓解、潜在碰撞严重性、自动驾驶车辆、路径规划、MPC、安全性
I.介绍
交通事故是世界上最危险的杀手，统计数据显示，每年世界上有数百万人在车辆的车轮下丧生。先进的驾驶辅助系统（ADAS），例如巡航控制，自适应巡航控制（ACC）和应用于高速公路驾驶和自动停车的协同ACC，应用于城市环境的盲角车辆检测，显着提高了安全性[1]。道路上的完全自动驾驶车辆（AV），无需人为干预，可以显着减少因驾驶员的错误、疲劳和醉酒驾驶引起的事故。完全避免交通事故仍然是不现实的，在不可避免的事故情况下，确定如何生成碰撞严重程度最低的路径是一个需要研究和解决的挑战。
根据车辆事故调查[2]，大多数事故现场可分为以下几类：前方车辆突然转弯或改变其车道而不显示转向信号；前车突然刹车；障碍物从前面的车辆上掉下来；与行人碰撞或与道路上的静态车碰撞。事故造成的损害取决于障碍物的性质（行人，汽车或道路边界等）、碰撞速度及其配置[3]。对于汽车碰撞，碰撞主要取决于碰撞速度、碰撞方向[4]、车辆不匹配[5]、驾驶员的特征（如性别，年龄和体重[6]），汽车大小[ 7]，以及车辆安全装置[8]。
在过去的几十年里，路径规划研究一直是一个热门话题[15]。路径规划采用了许多技术。这些路径规划方法可以分为三种：基于图搜索的规划器，基于采样的方法和内插曲线规划器。在基于图形搜索的规划器的范围内，Dijkstra算法是一种基于图形搜索的算法，可以在图形中找到单源最短路径[16];A *算法是一种基于图形搜索的算法，由于实现启发式算法，因而可以实现快速节点搜索[17]；并且状态点阵算法使用具有状态网格的规划区域的离散表示[18]。概率路线图方法（PRM）[19]和快速探索随机树（RRT）[20]是基于抽样的规划者最常用的方法。插值曲线规划器实现了路径平滑和曲线生成的不同技术，例如直线和圆[21]，回旋曲线和多项式曲线。
近年来，基于路径优化的技术已经成为最先进的AV路径规划方法，[ 9 ]。这项技术的核心是将路径规划问题表述为一个考虑多约束和预期车辆性能的优化问题。模型预测控制（MPC）已被证明非常适合解决路径规划问题，因为它们能够处理多约束和凸问题[10] [22]。此外，MPC以递归方式解决路径优化问题，同时考虑到规划过程中环境状态的更新。因此，MPC用于解决本论文中的路径规划问题。
据我们所知，碰撞缓解研究仍然是路径规划领域研究中的一个空白领域。我们为此合成了一种自动驾驶汽车MPC路径规划控制器，该控制器可以避开障碍物并生成一种具有不可避免的碰撞但可将严重性降到最低的紧急路径。在模型预测控制器中，预测碰撞严重程度、障碍物和道路边界的人工势场、路径跟踪矩阵和其他车辆性能约束被考虑到成本函数中。vwin 不同的场景以验证我们提出的控制策略能够生成既可以避开障碍物又可以减轻碰撞严重程度以保持自动车辆的最佳安全性的路径。
本论文研究了自动驾驶车辆的路径规划算法，以便在无法避免碰撞时减轻碰撞严重程度。第II节介绍了碰撞缓解路径规划的控制设计——包括车辆模型、碰撞严重度系数的定义、这里采用的潜在领域代表了路径规划的环境和控制设计。第III节介绍了两个案例研究，以验证拟议的减速路径规划控制策略，然后是第IV节的结论和未来工作。
II.路径规划
本节介绍基于碰撞缓解的自动驾驶车辆路径规划方法的控制设计。该过程包括车辆建模，严重性因子SF的定义，人工势场的引入和用于路径规划的MPC算法。
A.车辆建模
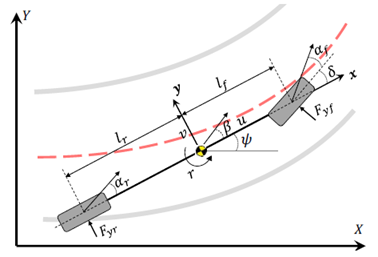
实际上，车辆动力学非常复杂，高保真度模型可能是高度非线性和不连续的。为了设计控制器，使用自行车模型。图1描绘了具有3个自由度的车辆模型图，即纵向，横向和偏航[11]：
图1.车辆自行车模型
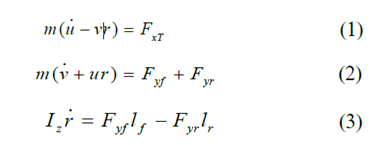
车辆相对于全局坐标的运动：
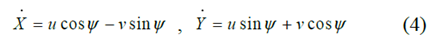
其中，m表示车辆的总质量，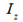
是车辆的偏航惯性矩；r，u和v分别是CG的横摆率、纵向的速度和横向速度。
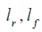分别是C.G.到前、后轴的距离。X和Y是纵向和横向的车辆位置，
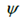是车辆的航向角，
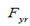和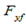
表示后轮胎和前轮胎的力，
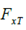是纵向轮胎力。
具有线性轮胎模型的前轮转向车辆的横向轮胎力可以计算为：
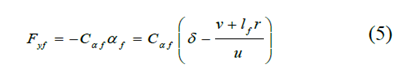
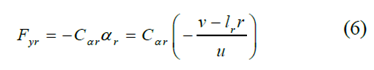
其中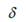
是输入转向角，
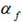表示前轮的侧滑角，
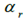表示后轮胎的侧滑角，
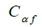和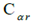
代表前后轮胎的转弯刚度。
B.潜在碰撞严重度指数PCSI的定义
如引言中所述，事故严重程度主要取决于碰撞速度，障碍物特征和碰撞配置（与停止的车辆、具有刚性固定障碍物、或与任何其他车辆的正面碰撞）。本文考虑了三个主要因素：碰撞速度，碰撞角度和两个碰撞车辆的质量比。
1）相对速度ΔV
许多速度相关指标被用来评估潜在的碰撞严重度，包括等效速度、能量等效速度、加速度严重度指数或乘员碰撞速度。根据美国，英国和澳大利亚的碰撞数据分析，与速度有关的碰撞严重程度是ΔV的函数，ΔV是碰撞时之前和之后的车速变化。相反，但本质上相同，在我们的算法中，采用接近速度作为ΔV的定义来测量潜在碰撞严重度指数( PCSI )：
其中，ΔV和D分别是接近速度和障碍车辆与自我车辆之间的距离。
2）相对航向角θ
数据库分析显示，最高碰撞风险发生在1/3重叠碰撞中，而等效障碍速度高于20英里/小时[13]。在上述分析的基础上, 为了便于实现, 我们将自我车辆与车辆障碍物之间的相对角θ定义为每辆车辆的航向角之和。与相对角度θ相关的潜在碰撞严重性指数定义如下：
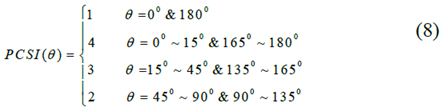
3）质量比Wo / W
就两辆车坠毁事故的不匹配而言，报告显示轻型卡车车辆的乘客死亡相对风险比乘用车撞车的风险高3至4倍[7]。关于与两种车辆的质量比相关的潜在碰撞严重性指数，我们可以简单地将其定义如下[14]：
其中Wo和W分别是障碍车辆和自我车辆的重量。因此，潜在的总碰撞严重度指数将是：
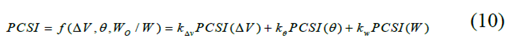
其中，A、B和C是潜在碰撞严重程度的重量参数，分别与相对速度、相对角度和质量比相关。
C.障碍描述
其中人工势场（PF）、不可穿越（U）、可穿越（UC）和道路（UR））定义的障碍有三种。势场可以计算为PF的总和[23]：
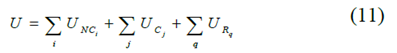
其中索引 i，j和q代表不能越过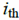
的障碍，可以跨越的障碍是
，
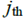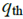表示车道标记。这三种PF的详细介绍如下：
a）不可穿越的障碍物：
不可穿越的障碍物，如车辆或行人，会造成不稳定、损坏车辆或威胁人们的生命，并且是安全距离SD的函数，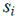
[ 12 ]：
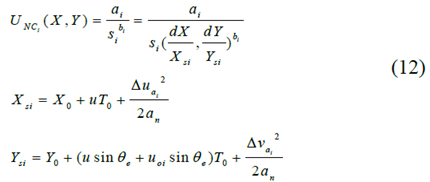
ｙ其中ai和bi分别是PF的形状和强度参数，Xsi表示与障碍物的纵向安全距离，Ysi是与障碍物的横向安全距离，Xo和Yo是最小纵向和横向距离。为了表示安全时间间隙，u表示自我车辆的速度，uoi是障碍物的速度，θe是朝向彼此的航向角。位于( 20m，2m )的不可穿越障碍物的势场如图2所示：
图2.不可穿越障碍物的PF
b )可穿越障碍物：
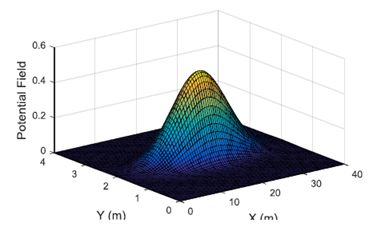
指数函数用于定义某些障碍物的PF，例如道路上的小碰撞或一些软垃圾不会对自我车辆造成任何损害：
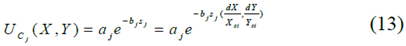
其中aj和bj是障碍物的形状和强度参数，sj表示类似于计算的障碍物和自我车辆之间的归一化安全距离（12）。位于( 10m，2m )的可穿越障碍物的势场如图3所示。
图3.可穿越障碍物的PF
c）道路边界：
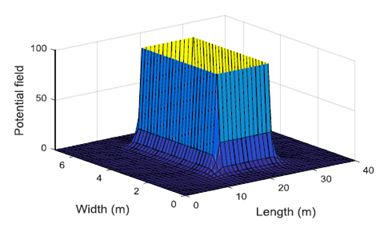
当自我车辆在道路上行驶时，尤其是在高速公路上行驶时，除非驾驶员想要改变车道，否则车辆不能越过道路车道标记。禁止撞击道路隔离带，因为它会导致不稳定或严重的车祸。为了避免不希望的道路交叉，道路边界的PF可以定义为：
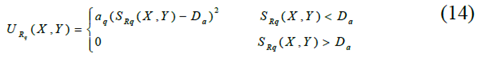
其中sRq是距离道路边界的车辆安全距离，Da是距离道路边界的允许距离，q表示右侧或左侧的车道标记，aq是强度参数。
利用二次函数来定义车道标记PF，当安全距离减小时，它们的梯度线性增加，如图4所示。
图4.道路边界的PF
D.路径规划的控制设计
本节采用模型预测控制算法进行路径规划。为了达到避障和最低碰撞严重程度的目的，根据目标函数计算出的碰撞严重性因子和人工势场。车辆动态也被认为是最优控制问题。基于上述分析，模型预测控制器可以优化指令跟踪、避障、车辆动态、道路调节，并利用预测值减轻不可避免的碰撞。
假设路径规划模块接受期望车道、速度、障碍物、道路边界和车辆状态的信息。
使用等式( 1 ) - ( 6 )，车辆在全局坐标中的动态可以以状态空间形式写成：
其中，
。横向和纵向速度v，u；车辆的航向角
和横摆率r。系统输入包括纵向轮胎力FxT和转向角δ。y是包括横向位置和速度的输出矩阵。
包括所需车道和目标纵向速度的所需输出矩阵，表示要跟踪的参考点如下所示：
其中ydes是所需的输出矩阵，包括所需的车辆横向位置Ydes和所需的速度udes。ldes是从右侧开始计算的所需车道索引号。Lw是车道的宽度。MPC的优点之一是它不仅能够处理对输入、状态和输出的限制。因此，包括道路规则、致动器容量约束和车辆动态约束在内的约束都被考虑到MPC问题中。
首先，根据道路规定，公路车辆不应违反最高和最低速度的要求。约束可以表示为：
其中umin和umax表示最小和最大允许速度。
此外，致动器容量被认为是：
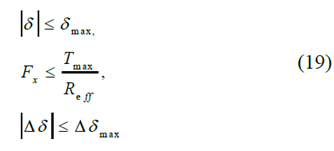
其中Reff表示车轮的半径; δmax表示最大转向角；Tmax是最大推进扭矩; △δ是一步中转向角的变化率，△δmax是其容量。纵向载荷传递效率包含在轮胎力椭圆约束中：
其中FxT_max表示最大总纵向轮胎力。Fyf0_max和Fyr0_max表示标称最大横向前后轮胎力。W是车辆的重量， h是C.G.的高度，μ是轮胎 - 路面摩擦系数。成本函数包括势场U，严重性因子SF，所需路径的跟踪，控制输入及其变化以及松弛变量如下所示：
其中t + k表示当前时间t之前的k个步长的预测值。Nc和Np分别表示控制范围和预测范围。
是k步的松弛变量向量，表示轮胎力的软约束的惩罚。目标函数包含潜在字段、碰撞严重程度、路径跟踪、输入、输入变化和松弛变量。其中，路径跟踪，输入，输入变化和松弛变量分别加权加权矩阵Q，R，S和用P加权的松弛变量的第一范数。通过（21.a）预测州。公式（21.b）生成输出，其中C是输出，D是前馈矩阵。在（21.d）中给出了对致动器的约束，车辆速度和轮胎容量约束的相应线性约束，其中ys是软约束变量向量并且还包括以提供对边界违反的许可。对应于致动器约束的松弛变量被设置为零，因为它们不能被违反。线性化约束可以作为（21.c）中输入和状态的函数写入，其中Ds和Cs分别表示前馈和输出矩阵。车速及其违规限制在（21.f）和（21.g）中表示。通过减少（21.h）中的控制输入数量可以降低计算成本，并且控制输入在第一个Nc预测步骤之后每Nrc步骤改变一次。
III.案例分析
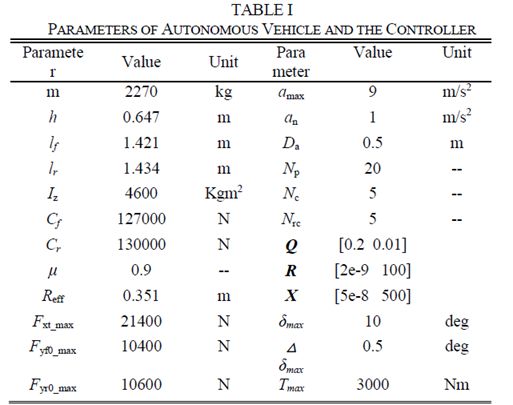
自动驾驶车辆和控制器的参数如表I所示。
案例研究1：如图5所示，自我车辆在车道1上以60km / h的速度起动，同时在车道2中间，前方10m处有一辆障碍车辆。1号车道的人行横道已满。然而，道路边界没有隔离带。在这种情况下，碰撞是不可避免的，因为车辆1和行人之间没有足够的空间停车，车道2也不清楚。
图5.案例研究1的示意图
使用工作中描述的方法，自我车辆的横向距离如图6所示。可以看出，车辆选择越过道路边界而不是撞击行人和左侧车辆。速度如图7所示，可以看出自我车辆也采用苛刻的制动来越过道路边界。图8展示了自我车辆的前轮胎力。
图6.自我车辆的横向距离
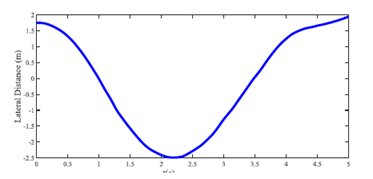
图7.自我车辆的纵向速度
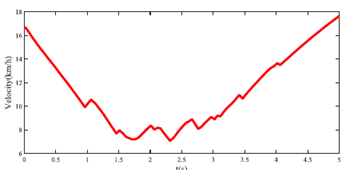
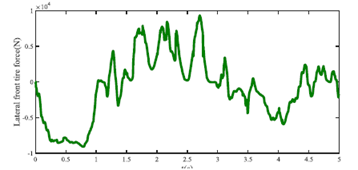
图8.自我车辆的横向前轮胎力
案例研究2：自我车辆在车道1上以60km / h的速度启动。在车道2的中间有一辆障碍车1，速度为25km / h，最初在X方向上在障碍物前方的10m处。人行横道部分和右侧人行道都被行人占用。与此同时，左侧人行道是空的。设计这样的情况使得自我车辆在停留在道路边界内时不能避开两个障碍物。示意图如图9所示。
图9.案例研究2的示意图
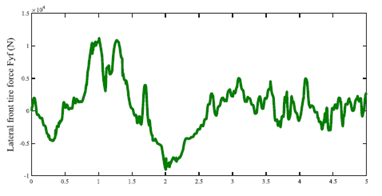
自我车辆的轨迹如图10所示。在这种情况下，自我车辆避免撞击行人并通过进入左车道来最小化事故严重性。图11显示了自我车辆的纵向速度。图12显示了自我车辆的前轮胎力。据我们所知，人类生命的保护是最重要的。仿真结果满足联网和自动驾驶车辆交通道德规则的要求。
图10.自我车辆的横向距离
图11.自我车辆的纵向速度
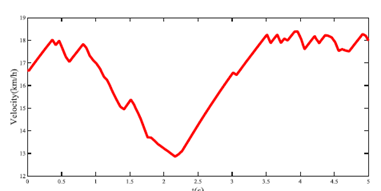
图12.自我车辆IV的横向前轮胎力。
IV.结论
本文提出了一种用于自动驾驶车辆的路径规划方法，尤其是当碰撞不可避免时，通过产生尽可能减轻碰撞的轨迹。假设运动规划模块从全局规划模块接收期望的车道和速度信息，并且从感知模块接收障碍物和道路边界的信息。本研究采用模型预测控制算法进行路径规划。为了达到避障的目的，将提出的描述障碍物的碰撞严重度因子和人工势场插入到成本函数中，如果避障是不可能的，则为最低碰撞严重度。此外，车辆动态也被考虑到该最优控制问题中以确保所产生的路径的可行性。仿真结果表明，MPC算法能够避开障碍物，并在碰撞不可避免的情况下减轻碰撞。这种拟议的路径规划方法正在进行实地测试，未来应该分析更多的城市情况，例如交通灯处的紧急情况。
致谢
作者要感谢安大略省研究基金会（ORF）和加拿大自然科学与工程研究委员会（NSERC）的慷慨赞助。
-
MPC
+关注
关注
2文章
36浏览量
21221 -
自动驾驶
+关注
关注
784文章
13784浏览量
166375
原文标题：自动驾驶汽车的本地路径规划：减少碰撞
文章出处：【微信号：IV_Technology，微信公众号：智车科技】欢迎添加关注！文章转载请注明出处。
发布评论请先 登录
相关推荐
工商网监
评论