以MSP430F499为核心的波形合成器设计方案-德赢Vwin官网网

随着电力电子技术的发展，对信号的要求越来越高。在某些场合，对于信号的频率，相位以及失真度要求较高。高质量信号的合成显得具有特殊的地位。"信号系统"课程中，周期连续信号的分解与合成是学习的难点。加深对理论知识的理解，提高学生实践能力、创新能力以及理论联系实际的能力，实验是必不可少的。已知周期信号的数学表达式，按照傅立叶级数可以分解为无穷多个不同频率不同振幅的正弦信号；反之，无穷多个不同频率、不同振幅的正弦波可以合成各种周期信号。本系统利用一些常规的芯片设计了一系列电路，可以实现周期连续信号的分解与合成。本系统既可以帮助低年级的同学学习周期信号的分解与合成，又可以运用于实际，信号质量高，具有实用价值。

1 波形合成器设计方案

1.1 该系统的基本原理

任何周期信号只要满足狄利克雷条件就可以分解成直流分量及许多正弦、余弦分量。这些正弦、余弦分量的频率必定是基频的整数倍。根据函数的对称性与傅里叶系数的关系知，周期对称方波信号可以用无穷个奇次谐波分量的傅里叶级数来表示：

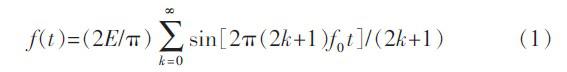
以MSP430F499为核心的波形合成器设计方案

周期对称三角波可以用无穷个奇次谐波分量的傅里叶级数来表示：

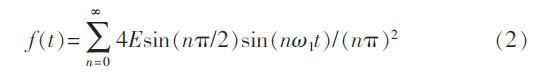
以MSP430F499为核心的波形合成器设计方案

在本系统中只用取出前两项奇次谐波，然后合成即可得到近似方波、三角波。

1.2 方波振荡电路

采用vwin 分立元件或单片压控函数发生器以及FPGA都可以产生方波，但是采用模拟器件由于元件分散性太大，参数也与外接部件有关，外接电阻电容对参数影响太大，影响系统的稳定性，故本系统用FPGA产生方波。FPGA系统板上有晶振，可以产生高精度高稳定度的基准频率。利用镇相环可以输出频率稳定的信号源，如果对输出信号再进行分频就可以得到步进频率较细的频率源。分频的方法可以使用锁相环来实现。操作方便，输出信号稳定性好，可以产生频率为晶振的约数的任意频率。

1.3 移相网络

移相是指对于两路同频信号，以其中一路为参考信号，另一路信号相对于该参考信号做超前或滞后的移相形成相位差。主要有数字移相法和RC移相两种。数字移相法通常采用延时的方法，以延时的长短来决定两路数字信号间的相位差。数字移相法移相量可以很大，但是在一个周期内采样点数较多，对AD和RAM的速度要求很高。用RC组成移相网络进行移相，由于回路呈容性，信号经过该网络后，相位发生变化。由于该方案简单，很方便实现-45°到+45°移相，足以满足需求，所以本系统采用了RC移相法。

1.4 滤波电路设计

滤波电路用八阶低通椭圆开关电容滤波器，椭圆滤波器相比其他类型的滤波器，在阶数相同的条件下有着最小的通带和阻带波动。巴特沃兹滤波器的幅度函数是单调下降的，但巴特沃兹滤波器能实现最大平坦幅度滤波；切比雪夫低通滤波器的幅度响应在通带内是在两个值之间波动，在通带内的波动次数取决予滤波器的阶数。为进一步减小高次谐波对有用信号的影响并保证通频带内最大平坦幅度滤波，在开关电容滤波器后加上巴特沃斯低通滤波器。

1.5 五选一通道选择

模拟开关和继电器都可以控制通道的选择。模拟开关的作用就是用在模拟信号的传输路径切换电路中，开关在电路中起接通信号和断开信号的作用。最常见的可控开关是继电器，当驱动继电器的电路加高电平或低电平时，继电器就吸合或释放，其触点接通或断井电路。CMOS模拟开关是半导体器件，它不像继电器那样可以用在大电流、大电压的场合，当输入信号过低或者过高时，MOSFET处于反向偏量，当电压达到一定值时（超过限制0.3 V），开关无法正常工作，因此模拟开关只适用于处理幅度不超过其工作电压、电流较小的模拟或数字信号。模拟开关的导通电阻随输入信号的变化而变化，对信号有一定的影响。继电器寿命高、灵敏度高、转换速度快、电磁干扰小，故本系统使用继电器进行通道切换。

1.6 检波方案的设计

常见的检波方法主要有两种：峰值检波和有效值检波。基本的峰值检波电路由二极管电路和电压跟随器组成，当输入电压正半周导通时，检波管导通，对电容充电。选择适当的电容值，使得电容充电速度大于放电速度，这样电容两端的电压可以保持在最大电压处从而实现峰值检波。峰值检波能检测的信号频率范圈很宽，被检测信号频率低时检波的纹波较大，且二极管是非线性元件，当交流电压较小时，检测的直流电压偏离其峰值较多。而采用有效值检波不仅可以直接测得各种波形的真实有效值，而且测量精度高。

2 系统整体方案设计

本系统用FPGA产生方波，分频后用八阶椭圆低通开关电容滤波器MAX297初步滤波，然后用三阶低通巴特沃斯滤波器进一步滤波。分频滤波后即可得到10 kHz、30 kHz、50 kHz的正弦波。可通过按键选择波形和合成阶数。通过RC移相网络使得信号产生确定的相位差，根据方波三角波各次谐波组成关系，把各次谐波叠加，即可得到近似方波和三角波。各次谐波信号依次经过峰值检波电路处理后送入单片机，单片机对分频滤波后的信号采样，经过一系列处理后，将峰值用LCD显示。系统框图如1所示。

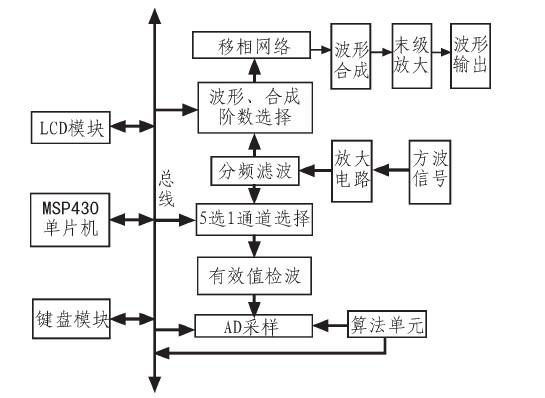
以MSP430F499为核心的波形合成器设计方案

图1 系统框图

3 系统硬件电路设计

3.1 整个系统中电源的去耦问题

在整个系统中会用到很多的运算放大器芯片。一般来说，运算放大器的供电电源端应连接去耦电容（对交流放大器尤其需要），以消除信号电流通过电源内阻给电路带来的影响。运算放大器的性能不同，其去耦电容的容量也有所不同。对于低速运算放大器，一般在紧靠运放供电端与电源地之间接容量为0.1μF的电容就可以了，但是对于高速运算放大器，应当在紧靠运放的供电端与电源地之间用容量为10μF和容量为0.01μF的电容器并联连接。整个系统中所有的运算放大器都做了去耦处理，只是画图中为简单起见，省略了去耦电容。

除此之外，运算放大器的地线连接也有讲究，对于小功率运放而言，地线连接无特殊要求，但对于较大功率的运算放大器，地线连接相当重要。总的原则是地线应短而粗并且在同一点连接。本系统中数字地模拟地共存，因此设计时将所有模拟地和数字地分别连接，最后电路中的模拟地和数字地与电源地一点汇集。

3.2 滤波电路

图2、图3中两个低通滤波器都是三阶巴特沃斯低通滤波器。有源滤波器适应在低频段（<100 kHz）的滤波，当频率较低时，若用无源滤波，电容、电感的元件值及体积都会很大，大电容电感不易获得，且误差较大，而有源滤波器则可以依靠运放在低频段的诸多优势（尤其是低噪声运放）达到很好的滤波效果。10 kHz、30 kHz、50 kHz信号经八阶椭圆开关电容滤波器滤波后，10 kHz、30 kHz、50 kHz信号再分别用理论截止频率为20kHz、35 kHz、55 kHz的低通滤波器滤波，理论值与实际截止频率有一定的偏差，为防止有用信号落在通频带之外，理论截止频率没有按照严格的10kHz和30kHz。

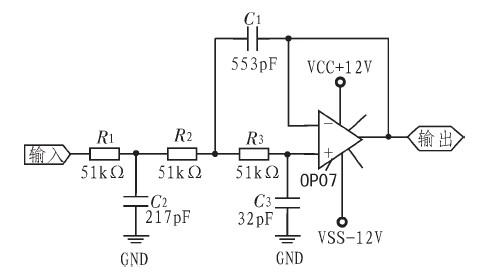
以MSP430F499为核心的波形合成器设计方案

图2 20kHz低通滤波器

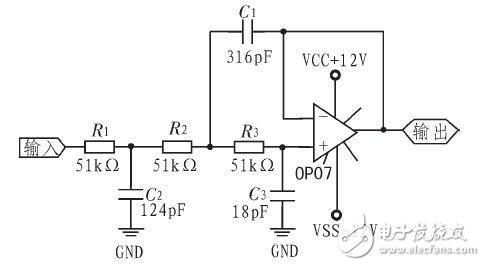
以MSP430F499为核心的波形合成器设计方案

图3 35kHz低通滤波器

3.3 移相电路

RC移相网络参数的计算：

要求叠加后的信号移相范围为-45°~+45°，设A信号为Asin（ωt+45°），B信号为Bsin（ωt+45°），叠加后的信号为

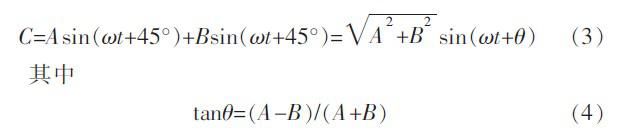
以MSP430F499为核心的波形合成器设计方案

改变A和B的值就可以改变叠加后信号的相位。

只有输入信号的频率与RC网络的谐振频率相同时，才会有45°的相移，因此随着输入信号频率的变化，RC网络的谐振频率也要相应的改变。根据公式

f=1/2πRC （5）

推导可得R值，取电容C为0.1μF,当输入信号的频率为100Hz时，R=16kΩ，当频率为1kHz时，R=1.6kΩ，当频率变为10kHz时，R=160Ω。

输入的正弦信号经过RC构成的超前和滞后网络后经过运放（OPA37）构成的射极跟随器，然后通过电位器R3叠加，再经过放大电路通过一个电位器输出。电路图如图4所示。

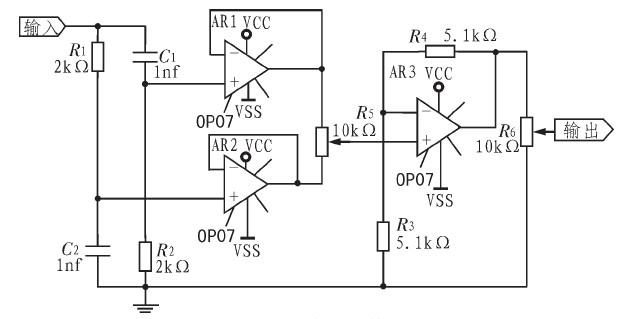
以MSP430F499为核心的波形合成器设计方案

图4 移相网络

3.4 加法器

此加法器为同相加法器，由于集成运放可视为理想运放，其输入端可视为虚短和虚开路。在同向端运用节点电流方程可求得输出：

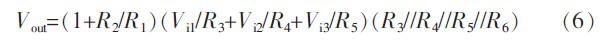
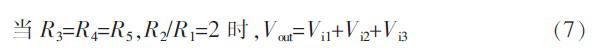
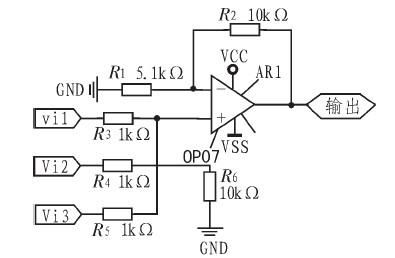
以MSP430F499为核心的波形合成器设计方案

图5 加法器

3.5 有效值检波

有效值检波采用真有效值/直流转换芯片AD637能计算任何复杂波形的真有效值、平均值、均方值、绝对值，具有分贝输出（0~60 dB）。具有宽频带，量程在0~7 V范围内可调。

AD637内部结构包括有源整流器（即绝对值电路），平方/除法器、滤波放大器、独立的缓冲放大器、偏置电路五部分。使用AD637在测量峰值系数高达10的信号时附加误差仅为1%,且外围元件少、频带宽。对于有效值为200 mV的信号，-3dB带宽为600kHz;对于有效值为1V的信号。-3dB带宽为8MHz.该方案硬件简单，两且精度很高，效果理想。

4 系统软件设计

软件流程图见图6,本系统选用MSP430F449单片机，主要负责对方波、三角波10k、30k、50k等各次谐波连行采样，并用LCD12864对各次谐波的峰值显示；在程序运行的过程中，可通过16x16矩阵键盘控制选择波形及阶数的切换。

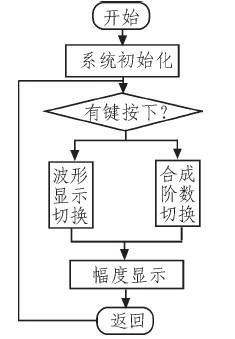
以MSP430F499为核心的波形合成器设计方案