DataCamp的Sayak Paul带你入门张量、PyTorch。
在深度学习中,常常看到张量是数据结构的基石这一说法。Google的机器学习库TensorFlow甚至都以张量(tensor)命名。张量是线性代数中用到的一种数据结构,类似向量和矩阵,你可以在张量上进行算术运算。
PyTorch(Facebook创建的python包,提供两个高层特性:1) 类似Numpy的基于GPU加速的张量运算 2) 在基于回放(tape-based)的自动微分系统之上构建的深度神经网络。
本教程将介绍什么是张量,如何在PyTorch中操作张量:
张量介绍
PyTorch介绍
PyTorch安装步骤
PyTorch下的一些张量操作
基于PyTorch实现一个简单的神经网络
闲话少叙,让我们开始介绍张量吧。
张量介绍
张量是向量和矩阵的推广,可以理解为多维数组。知名的《深度学习》(Goodfellow等编写)是这样介绍张量的:
在一般意义上,以基于可变数目的轴的规则网格组织的一组数字称为张量。
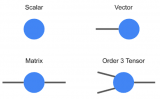
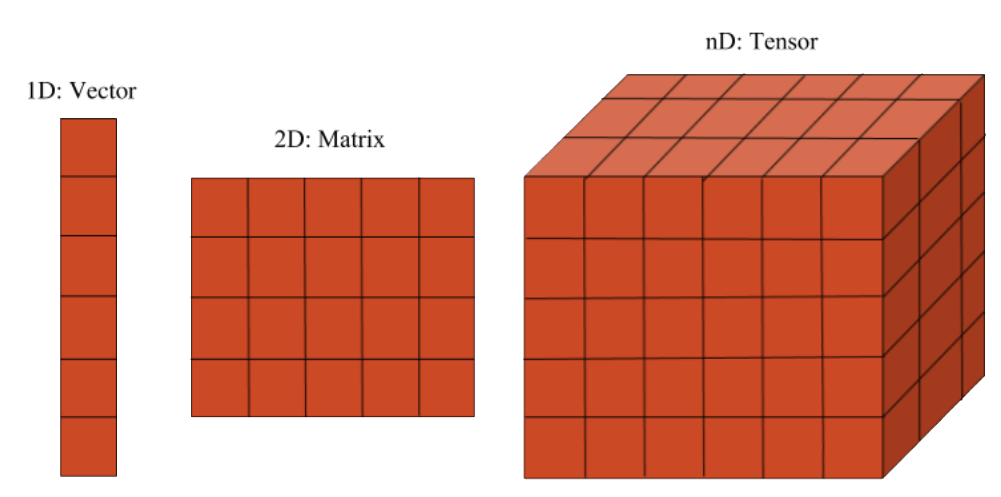
标量是零阶张量。向量是一阶张量,矩阵是二阶张量。
下面是张量的示意图:
现在让我们以更清晰易懂的方式构建张量背后的直觉。
张量是现代机器学习的基本构建。它是一个数据容器,大多数情况下包含数字,有时可能包含字符串(不过这罕见)。所以可以把张量想象成一桶数字。
人们经常混用张量和多维数组。不过有时需要严格区分两者,如StackExchange指出:
张量和多维数组是不同类型的对象。前者是一种函数,后者是适宜在坐标系统中表示张量的一种数据结构。
在数学上,张量由多元线性函数定义。一个多元线性函数包含多个向量变量。张量域是张量值函数。更严谨的数学解释,可以参考https://math.stackexchange.com/q/10282
所以,张量是需要定义的函数或容器。实际上,当数据传入时,计算才真正发生。当不需要严格区分数组和张量的时候,数组或多维数组(1D, 2D, …, ND)一般可以视作张量。
现在我们稍微讲下张量表述(Tensor notation)。
张量表述和矩阵类似,一般用大写字母表示张量,带整数下标的小写字母表示张量中的标量值。
标量、向量、矩阵的许多运算同样适用于张量。
张量和张量代数是物理和工程领域广泛使用的工具。机器学习的许多技术,深度学习模型的训练和操作,常常使用张量这一术语进行描述。
PyTorch介绍
PyTorch是一个非常灵活的基于Python的深度学习研究平台。
PyTorch特性
提供各种张量的常规操作。
基于回放的自动微分系统。
不同于TensorFlow、Theano、Caffe、CNTK等大多数框架采用的静态图系统,PyTorch采用动态图系统。
最小化框架开销,可基于GPU加速。
相比Torch等替代品,PyTorch的内存使用非常高效。这让你可以训练比以往更大的深度学习模型。
Kirill Dubovikov写的PyTorch vs TensorFlow — spotting the difference比较了PyTorch和TensorFlow这两个框架。如果你想了解TensorFlow,可以看看Karlijn Willems写的教程TensorFlow Tutorial For Beginners。
PyTorch安装步骤
PyTorch的安装很简单。如果你的显卡支持,可以安装GPU版本的PyTorch。
你可以使用pip安装torch、torchvision这两个包,也可以使用conda安装pytorch torchvision这两个包。注意,Windows平台上,PyTorch不支持Python 2.7,需要基于Python 3.5以上的版本安装。
具体的安装命令可以通过PyTorch官网查询: https://pytorch.org/get-started/locally/
好了,下面让我们直接深入PyTorch下的一些张量算术。
PyTorch下的一些张量操作
首先,导入所需的库:
import torch
如果出现报错,说明PyTorch没有安装成功,请参考上一节重新安装。
现在,我们构造一个5×3的矩阵:
x = torch.rand(5, 3)
print(x)
输出:
tensor([[ 0.5991, 0.9365, 0.6120],
[ 0.3622, 0.1408, 0.8811],
[ 0.6248, 0.4808, 0.0322],
[ 0.2267, 0.3715, 0.8430],
[ 0.0145, 0.0900, 0.3418]])
再构造一个5×3的矩阵,不过这次用零初始化,并指定数据类型为long:
x = torch.zeros(5, 3, dtype=torch.long)
print(x)
输出:
tensor([[ 0, 0, 0],
[ 0, 0, 0],
[ 0, 0, 0],
[ 0, 0, 0],
[ 0, 0, 0]])
构造张量时直接提供数据:
x = torch.tensor([5.5, 3])
print(x)
输出:
tensor([ 5.5000, 3.0000])
如果你想检验下自己是否理解了PyTorch中的张量,那可以思考下上面的张量x是什么类别的。
基于已有张量,可以创建新张量——新张量会复用输入张量的属性,比如dtype(数据类型),除非另外给出新值:
x = x.new_ones(5, 3, dtype=torch.double)
print(x)
x = torch.randn_like(x, dtype=torch.float)
print(x)
输出:
tensor([[ 1., 1., 1.],
[ 1., 1., 1.],
[ 1., 1., 1.],
[ 1., 1., 1.],
[ 1., 1., 1.]], dtype=torch.float64)
tensor([[-1.2174, 1.1807, 1.4249],
[-1.1114, -0.8098, 0.4003],
[ 0.0780, -0.5011, -1.0985],
[ 1.8160, -0.3778, -0.8610],
[-0.7109, -2.0509, -1.2079]])
获取张量的尺寸:
print(x.size())
输出:
torch.Size([5, 3])
注意,torch.Size事实上是一个元组,支持所有元组操作。
现在,让我们看下张量的加法。
张量加法
两个张量分素相加,得到维度一致的张量,结果张量中每个标量的值是相应标量的和。
y = torch.rand(5, 3)
print(x)
print(y)
print(x + y)
输出:
tensor([[-1.2174, 1.1807, 1.4249],
[-1.1114, -0.8098, 0.4003],
[ 0.0780, -0.5011, -1.0985],
[ 1.8160, -0.3778, -0.8610],
[-0.7109, -2.0509, -1.2079]])
tensor([[ 0.8285, 0.7619, 0.1147],
[ 0.1624, 0.8994, 0.6119],
[ 0.2802, 0.2950, 0.7098],
[ 0.8132, 0.3382, 0.4383],
[ 0.6738, 0.2022, 0.3264]])
tensor([[-0.3889, 1.9426, 1.5396],
[-0.9490, 0.0897, 1.0122],
[ 0.3583, -0.2061, -0.3887],
[ 2.6292, -0.0396, -0.4227],
[-0.0371, -1.8487, -0.8815]])
除了使用+运算符外,也可以调用torch.add方法(两者是等价的):
print(torch.add(x, y))
下面我们来看张量减法。
张量减法
两个张量分素相减,得到维度一致的张量,结果张量中每个标量的值是相应标量之差。
接着我们将讨论张量相乘。
张量乘法
假设mat1是一个(n×m)的张量,mat2是一个(m×p)的张量,两者相乘,将得到一个(n×p)的张量。
mat1 = torch.randn(2, 3)
mat2 = torch.randn(3, 3)
print(mat1)
print(mat2)
print(torch.mm(mat1, mat2))
输出:
tensor([[ 1.9490, -0.6503, -1.9448],
[-0.7126, 1.0519, -0.4250]])
tensor([[ 0.0846, 0.4410, -0.0625],
[-1.3264, -0.5265, 0.2575],
[-1.3324, 0.6644, 0.3528]])
tensor([[ 3.6185, -0.0901, -0.9753],
[-0.8892, -1.1504, 0.1654]])
注意,torch.mm()不支持广播(broadcast)。
广播
“广播”这一术语用于描述如何在形状不一的数组上应用算术运算。在满足特定限制的前提下,较小的数组“广播至”较大的数组,使两者形状互相兼容。广播提供了一个向量化数组操作的机制,这样遍历就发生在C层面,而不是Python层面。广播可以避免不必要的数据复制,通常导向高效的算法实现。不过,也存在不适用广播的情形(可能导致拖慢计算过程的低效内存使用)。
可广播的一对张量需满足以下规则:
每个张量至少有一个维度。
迭代维度尺寸时,从尾部的维度开始,维度尺寸或者相等,或者其中一个张量的维度尺寸为一,或者其中一个张量不存在这个维度。
让我们通过几段代码来理解PyTorch的广播机制。
x=torch.empty(5,7,3)
y=torch.empty(5,7,3)
相同形状的张量总是可广播的,因为总能满足以上规则。
x=torch.empty((0,))
y=torch.empty(2,2)
不可广播(x不满足第一条规则)。
# 为了清晰易读,可以对齐尾部
x=torch.empty(5,3,4,1)
y=torch.empty( 3,1,1)
x和y可广播:
倒数第一个维度:两者的尺寸均为1
倒数第二个维度:y尺寸为1
倒数第三个维度:两者尺寸相同
倒数第四个维度:y该维度不存在
但下面一对就不可广播了:
x=torch.empty(5,2,4,1)
y=torch.empty( 3,1,1)
这是因为倒数第三个维度:2 != 3
现在你对“可广播”这一概念已经有所了解了,让我们看下,广播后的张量是什么样的。
如果张量x和张量y是可广播的,那么广播后的张量尺寸按照如下方法计算:
如果x和y的维数不等,在维数较少的张量上添加尺寸为1的维度。结果维度尺寸是x和y相应维度尺寸的较大者。例如:
x=torch.empty(5,1,4,1)
y=torch.empty( 3,1,1)
(x+y).size()
输出:
torch.Size([5, 3, 4, 1])
再如:
x=torch.empty(1)
y=torch.empty(3,1,7)
(x+y).size()
输出:
torch.Size([3, 1, 7])
再看一个不可广播的例子:
x=torch.empty(5,2,4,1)
y=torch.empty(3,1,1)
(x+y).size()
报错:
---------------------------------------------------------------------------
RuntimeError Traceback (most recent call last)
1 x=torch.empty(5,2,4,1)
2 y=torch.empty(3,1,1)
----> 3 (x+y).size()
RuntimeError: The size of tensor a (2) must match the size of tensor b (3) at non-singleton dimension 1
你现在应该已经掌握了广播这个概念了!
张量乘积是最常见的张量乘法,但也存在其他种类的张量乘法,例如张量点积和张量缩并。
借助Numpy桥,PyTorch张量和NumPy数组之间的互相转换极其迅速。下面就让我们来了解一下这个概念。
NumPy桥
NumPy桥使得PyTorch张量和NumPy数组共享底层内存地址,对其中之一的修改会反映到另一个上。
转换PyTorch张量至NumPy数组。
a = torch.ones(5)
b = a.numpy()
print(a)
print(b)
输出:
tensor([ 1., 1., 1., 1., 1.])
[1.1.1.1.1.]
在这一节中,我们讨论了一些基本的张量算术,例如加法、减法、张量乘积。下一节我们将使用PyTorch实现一个基本的神经网络。
基于PyTorch实现一个简单的神经网络
如果你想要温习一下神经网络的概念,可以参考以下文章:
初窥神经网络内部机制
从头开始搭建三层神经网络
基于Numpy实现神经网络:反向传播、梯度下降
在实现神经网络之前,我们先来讨论一下自动微分,这是PyTorch下所有神经网络的核心,在进行反向传播计算梯度时尤其有用。
PyTorch的autograd模块为张量的所有运算提供了自动微分。这是一个define-by-run框架,也就是说,反向传播由代码如何运行定义,每个迭代都可以不一样。
让我们直接用代码展示自动微分是如何工作的。
x = torch.ones(2, 2, requires_grad=True)
print(x)
输出:
tensor([[ 1., 1.],
[ 1., 1.]])
进行加法运算:
y = x + 2
print(y)
输出:
tensor([[ 3., 3.],
[ 3., 3.]])
再进行一些运算:
z = y * y * 3
out = z.mean()
print(z)
print(out)
输出:
tensor([[ 27., 27.],
[ 27., 27.]])
tensor(27.)
现在让我们进行反向传播:
out.backward()
print(x.grad)
自动微分给出的梯度为:
tensor([[ 4.5000, 4.5000],
[ 4.5000, 4.5000]])
感兴趣的读者可以手工验证下梯度。
了解了PyTorch如何进行自动微分之后,让我们使用PyTorch编码一个简单的神经网络。
我们将创建一个简单的神经网络,包括一个隐藏层,一个输出层。隐藏层使用ReLU激活,输出层使用sigmoid激活。
构建神经网络需要引入torch.nn模块:
import torch.nn as nn
接着定义网络层尺寸和batch尺寸:
n_in, n_h, n_out, batch_size = 10, 5, 1, 10
现在生成一些输入数据x和目标数据y,并使用PyTorch张量存储这些数据。
x = torch.randn(batch_size, n_in)
y = torch.tensor([[1.0], [0.0], [0.0], [1.0], [1.0], [1.0], [0.0], [0.0], [1.0], [1.0]])
接下来,只需一行代码就可以定义我们的模型:
model = nn.Sequential(nn.Linear(n_in, n_h),
nn.ReLU(),
nn.Linear(n_h, n_out),
nn.Sigmoid())
我们创建了一个输入 -> 线性 -> relu -> 线性 -> sigmoid的模型。对于需要更多自定义功能的更加复杂的模型,可以定义一个类,具体请参考PyTorch文档。
现在,我们需要构造损失函数。我们将使用均方误差:
criterion = torch.nn.MSELoss()
然后定义优化器。我们将使用强大的随机梯度下降算法,学习率定为0.01.model.parameters()会返回一个模型参数(权重、偏置)上的迭代器。
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
下面我们跑50个epoch,这依次包括前向传播、损失计算、反向传播和参数更新。
for epoch in range(50):
# 前向传播
y_pred = model(x)
# 计算并打印损失
loss = criterion(y_pred, y)
print('epoch: ', epoch,' loss: ', loss.item())
# 梯度归零
optimizer.zero_grad()
# 反向传播
loss.backward()
# 更新参数
optimizer.step()
输出:
epoch: 0 loss: 0.2399429827928543
epoch: 1 loss: 0.23988191783428192
epoch: 2 loss: 0.23982088267803192
epoch: 3 loss: 0.2397598922252655
epoch: 4 loss: 0.23969893157482147
epoch: 5 loss: 0.23963800072669983
epoch: 6 loss: 0.23957709968090057
epoch: 7 loss: 0.23951618373394012
epoch: 8 loss: 0.23945537209510803
epoch: 9 loss: 0.23939454555511475
epoch: 10 loss: 0.23933371901512146
epoch: 11 loss: 0.23927298188209534
epoch: 12 loss: 0.23921218514442444
epoch: 13 loss: 0.23915143311023712
epoch: 14 loss: 0.2390907108783722
epoch: 15 loss: 0.23903003334999084
epoch: 16 loss: 0.23896940052509308
epoch: 17 loss: 0.23890872299671173
epoch: 18 loss: 0.23884813487529755
epoch: 19 loss: 0.23878750205039978
epoch: 20 loss: 0.23872694373130798
epoch: 21 loss: 0.2386663407087326
epoch: 22 loss: 0.2386058121919632
epoch: 23 loss: 0.23854532837867737
epoch: 24 loss: 0.23848481476306915
epoch: 25 loss: 0.23842433094978333
epoch: 26 loss: 0.2383638620376587
epoch: 27 loss: 0.23830339312553406
epoch: 28 loss: 0.2382429838180542
epoch: 29 loss: 0.23818258941173553
epoch: 30 loss: 0.2381247729063034
epoch: 31 loss: 0.2380656749010086
epoch: 32 loss: 0.23800739645957947
epoch: 33 loss: 0.2379491776227951
epoch: 34 loss: 0.2378900945186615
epoch: 35 loss: 0.23783239722251892
epoch: 36 loss: 0.23777374625205994
epoch: 37 loss: 0.23771481215953827
epoch: 38 loss: 0.23765745759010315
epoch: 39 loss: 0.23759838938713074
epoch: 40 loss: 0.23753997683525085
epoch: 41 loss: 0.2374821901321411
epoch: 42 loss: 0.23742322623729706
epoch: 43 loss: 0.23736533522605896
epoch: 44 loss: 0.23730707168579102
epoch: 45 loss: 0.23724813759326935
epoch: 46 loss: 0.23719079792499542
epoch: 47 loss: 0.23713204264640808
epoch: 48 loss: 0.23707345128059387
epoch: 49 loss: 0.2370160073041916
PyTorch的写法很清晰,配上注释,应该不难理解。如果仍有不解之处,可以参考下面的讲解:
y_pred获取模型一次前向传播的预测值。y_pred和目标变量y一起传给criterion以计算损失。
接着,optimizer.zero_grad()清空上一次迭代的梯度。
接下来的loss.backward()集中体现了PyTorch的神奇之处——这里用到了PyTorch的Autograd(自动计算梯度)特性。Autograd基于动态创建的计算图自动计算所有参数上的梯度。总的来说,这一步进行的是梯度下降和反向传播。
最后,我们调用optimizer.step(),使用新的梯度更新一次所有参数。
恭喜你读到了这篇长文的结尾。这篇文章从张量讲到了自动微分,同时基于PyTorch及其张量系统实现了一个简单的神经网络。
如果你想了解更多关于PyTorch的内容,或想进一步深入,请阅读PyTorch的官方文档和教程,这些文档和教程写得非常好。你可以从PyTorch官网找到这些文档和教程。
撰写这篇教程的时候,我参考了以下内容:
Daniel A. Fleisch的《A Student's Guide to Vectors and Tensors》
PyTorch官方文档
Jason Brownlee写的A Gentle Introduction to Tensors for Machine Learning with NumPy
如果有问题要问,或者有想法要讨论,欢迎留言!
如果你打算进一步学习Python,可以参加DataCamp的Statistical Thinking in Python课程。
-
张量
+关注
关注
0文章
7浏览量
2562 -
pytorch
+关注
关注
2文章
807浏览量
13196
原文标题:从张量到自动微分:PyTorch入门教程
文章出处:【微信号:jqr_AI,微信公众号:论智】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
张量计算在神经网络加速器中的实现形式
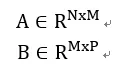
RK3568国产处理器 + TensorFlow框架的张量创建实验案例分享
TensorFlow获取张量形状的操作tfshape属性shape及方法
TensorFlow教程|张量的阶、形状、数据类型
一种张量总变分的模糊图像盲复原算法
基于TTr1SVD的张量奇异值分解
谷歌宣布开源张量计算库TensorNetwork及其API
基于张量的车辆交通数据缺失估计方法
什么是张量处理单元(TPU)
如何使用张量核在CUDA C++设备代码中编程
PyTorch的简单实现
张量类Tensor的实现
GPU的张量核心: 深度学习的秘密武器





 什么是张量,如何在PyTorch中操作张量?
什么是张量,如何在PyTorch中操作张量?










评论