最大功率传输分析-德赢Vwin官网网

当负载的电阻值等于电压源内部电阻的值，允许提供最大功率时，发生最大功率传输，通常，此源电阻甚至阻抗如果涉及电感器或电容器具有欧姆的固定值。

然而，当我们连接负载电阻时， R L 穿过在电源的输出端子中，负载的阻抗将从开路状态变化到短路状态，导致负载吸收的功率变得依赖于实际电源的阻抗。然后，为了使负载电阻能够吸收可能的最大功率，它必须与电源的阻抗“匹配”，这构成了最大功率传输的基础。

最大功率传输定理是另一种有用的电路分析方法，用于确保当负载电阻值恰好等于电源电阻时，最大功率消耗将在负载电阻中消耗。负载阻抗与能量源的内部阻抗之间的关系将给出负载中的功率。考虑下面的电路。

Thevenins等效电路

在上面的戴维宁等效电路中，最大功率传递定理表明，“如果它与提供功率的网络的Thevenin或Norton源电阻的值相等，则负载电阻中的最大功率消耗将消耗。” / p>

换句话说，导致最大功耗的负载电阻必须等于相当于戴维宁源电阻的值，然后 R L = R S 但如果负载电阻值低于或高于网络的戴维宁源电阻，则其耗散功率将小于最大值。

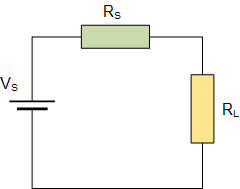
例如，找到值负载电阻 R L 将在以下电路中提供最大功率传输。

最大功率传输示例No1

Whe re：
R S =25Ω
R L 可在0 - 100Ω之间变化> V S = 100v

然后使用以下方法欧姆定律方程：

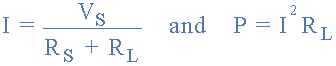
我们现在可以完成下表来确定电路中不同负载电阻值的电流和功率。

电流对表

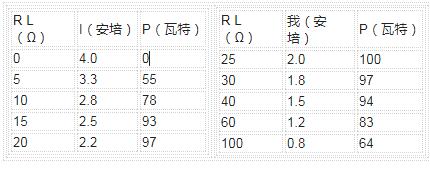
使用上表中的数据，我们可以绘制一个负载图对于不同的负载电阻值，电阻 R L ， P 。另请注意，开路时功率为零（零电流）条件）以及短路（零电压条件）。

电源负载电阻图

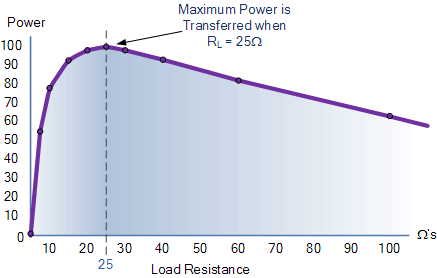
从上表和图表中可以看出，当负载电阻 R L <时，负载中出现最大功率传输/ span>的值与源电阻相等， R S ： R S = R L =25Ω。这被称为“匹配条件”，并且作为一般规则，当外部设备的阻抗时，最大功率从诸如电源或电池的有源设备传输到外部设备。完全匹配源的阻抗。

一个很好的例子阻抗匹配的le在音频放大器和扬声器之间。放大器的输出阻抗 Z OUT 可以在4Ω和8Ω之间给出，而标称输入扬声器的阻抗 Z IN 可能仅为8Ω。

然后，如果8Ω扬声器连接到放大器输出端，放大器将把扬声器视为8Ω负载。并联两个8Ω扬声器相当于驱动一个4Ω扬声器的放大器，两种配置均在放大器的输出规格范围内。

阻抗不当匹配会导致过多的功率损耗和散热。但是，如何阻抗匹配具有非常不同阻抗的放大器和扬声器。那么，有可用的扬声器阻抗匹配变压器，可以将阻抗从4Ω改变到8Ω，或者16Ω，以允许连接的许多扬声器的阻抗匹配各种组合，例如PA（公共广播）系统。

变压器阻抗匹配

阻抗匹配的一个非常有用的应用，以便在信号源和信号源之间提供最大的功率传输。负载处于放大器电路的输出级。信号变压器用于将扬声器的较高或较低阻抗值与放大器输出阻抗相匹配，以获得最大声功率输出。这些音频信号变压器称为“匹配变压器”，并将负载耦合到放大器输出，如下所示。

变压器阻抗匹配

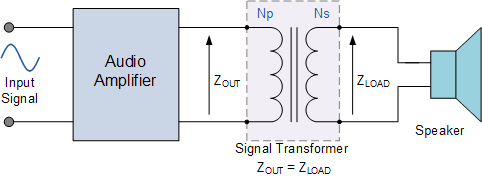
即使输出阻抗与负载阻抗不同，也可以获得最大功率传输。这可以通过变压器上合适的“匝数比”来实现，相应的负载阻抗比率 Z LOAD 与输出阻抗， Z OUT 匹配变压器初级匝数与次级匝数之比，因为变压器一侧的电阻变为另一侧的不同值。

如果负载阻抗， Z LOAD 是纯电阻性的，源阻抗是纯电阻性的， Z OUT 然后找到最大值的等式权力转移如下：

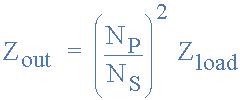
其中： N P 是初级匝数和 N S 变压器上的次级匝数。然后，通过改变变压器匝数比的值，输出阻抗可以与源阻抗“匹配”，以实现最大功率传输。例如，

最大功率传输示例No2

如果要将8Ω扬声器连接到输出阻抗1000Ω<的放大器/ span>，计算提供音频信号最大功率传输所需的匹配变压器的匝数比。假设放大器源阻抗 Z 1 ，负载阻抗 Z 2 ，匝数比为<跨度>名词

通常，低功率放大器电路中使用的小型高频音频变压器几乎总是被认为是简单的理想选择，因此可以忽略任何损耗。

声明：本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人，不代表德赢Vwin官网网立场。文章及其配图仅供工程师学习之用，如有内容侵权或者其他违规问题，请联系本站处理。举报投诉

最大功率传输分析