傅里叶级数的数学推导公式
但傅里叶级数在数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学等领域都有着广泛的应用，这不由得让人肃然起敬。一打开《信号与系统》、《锁相环原理》等书籍，动不动就跳出一个“傅里叶级数”或“傅里叶变换”，弄一长串公式，让人云山雾罩。
如下就是傅里叶级数的公式：
不客气地说，这个公式可以说是像“臭婆娘的裹脚布——又臭又长”，而且来历相当蹊跷，不知那个傅里叶什么时候灵光乍现，把一个周期函数f(t)硬生生地写成这么一大堆东西。单看那个①式，就是把周期函数f(t)描述成一个常数系数a0、及1倍ω的sin和cos函数、2倍ω的sin和cos函数等、到n倍ω的sin和cos函数等一系列式子的和，且每项都有不同的系数，即An和Bn，至于这些系数，需要用积分来解得，即②③④式，不过为了积分方便，积分区间一般设为[-π, π]，也相当一个周期T的宽度。
能否从数学的角度推导出此公式，以使傅里叶级数来得明白些，让我等能了解它的前世今生呢?下面来详细解释一下此公式的得出过程：
1、把一个周期函数表示成三角级数：
首先，周期函数是客观世界中周期运动的数学表述，如物体挂在弹簧上作简谐振动、单摆振动、无线电电子振荡器的电子振荡等，大多可以表述为：
f(x)=A sin(ωt+ψ)
这里t表示时间，A表示振幅，ω为角频率，ψ为初相(与考察时设置原点位置有关)。
然而，世界上许多周期信号并非正弦函数那么简单，如方波、三角波等。傅叶里就想，能否用一系列的三角函数An sin(nωt+ψ)之和来表示那个较复杂的周期函数f(t)呢?因为正弦函数sin可以说是最简单的周期函数了。于是，傅里叶写出下式：(关于傅里叶推导纯属猜想)
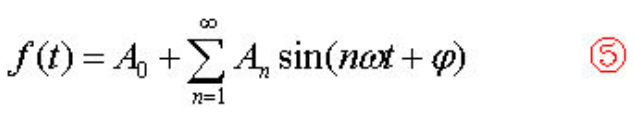
这里，t是变量，其他都是常数。与上面最简单的正弦周期函数相比，5式中多了一个n，且n从1到无穷大。这里f(t)是已知函数，也就是需要分解的原周期函数。从公式5来看，傅里叶是想把一个周期函数表示成许多正弦函数的线性叠加，这许许多多的正弦函数有着不同的幅度分量(即式中An)、有不同的周期或说是频率(是原周期函数的整数倍，即n)、有不同的初相角(即ψ)，当然还有一项常数项(即A0)。要命的是，这个n是从1到无穷大，也就是是一个无穷级数。
应该说，傅里叶是一个天才，想得那么复杂。一般人不太会把一个简单的周期函数弄成这么一个复杂的表示式。但傅里叶认为，式子右边一大堆的函数，其实都是最简单的正弦函数，有利于后续的分析和计算。当然，这个式能否成立，关键是级数中的每一项都有一个未知系数，如A0、An等，如果能把这些系数求出来，那么5式就可以成立。当然在5式中，唯一已知的就是原周期函数f(t),那么只需用已知函数f(t)来表达出各项系数，上式就可以成立，也能计算了。
于是乎，傅里叶首先对式5作如下变形：
这样，公式5就可以写成如下公式6的形式：
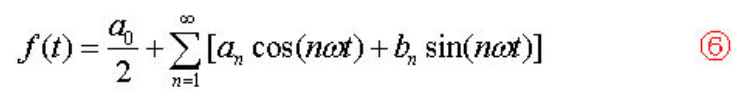
这个公式6就是通常形式的三角级数，接下来的任务就是要把各项系数an和bn及a0用已知函数f(t)来表达出来。
2、三角函数的正交性：
这是为下一步傅里叶级数展开时所用积分的准备知识。一个三角函数系：1，cosx , sinx , cos2x , sin2x , … , cosnx , sinnx , … 如果这一堆函数(包括常数1)中任何两个不同函数的乘积在区间[-π, π]上的积分等于零，就说三角函数系在区间[-π, π]上正交，即有如下式子：
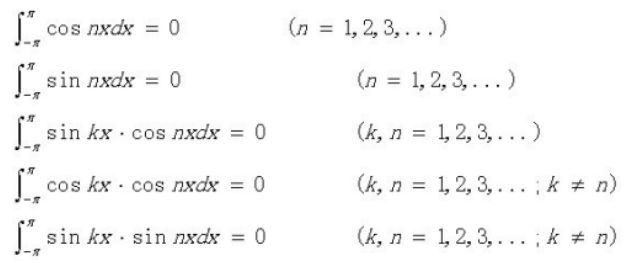
以上各式在区间[-π, π]的定积分均为0，第1第2式可视为三角函数cos和sin与1相乘的积分;第3-5式则为sin和cos的不同组合相乘的积分式。除了这5个式子外，不可能再有其他的组合了。注意，第4第5两个式中，k不能等于n，否则就不属于“三角函数系中任意两个不同函数”的定义了，变成同一函数的平方了。但第3式中，k与n可以相等，相等时也是二个不同函数。下面通过计算第4式的定积分来验证其正确性，第4式中二函数相乘可以写成：
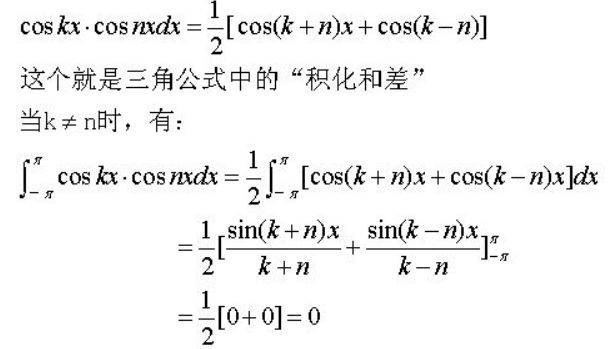
可见在指定[-π, π]的区间里，该式的定积分为0。其他式也可逐一验证。
3、函数展开成傅里叶级数：
先把傅里叶级数表示为下式，即⑥式：
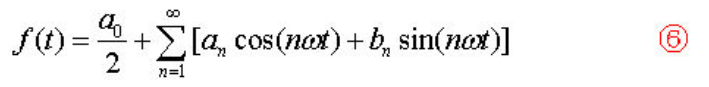
对⑥式从[-π, π]积分，得：
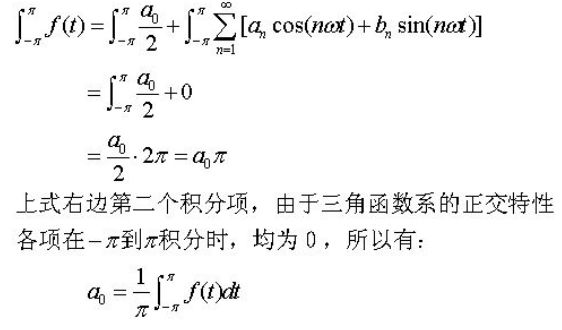
这就求得了第一个系数a0的表达式，即最上边傅里叶级数公式里的②式。接下来再求an和bn的表达式。用cos(kωt)乘⑥式的二边得：
至此，已经求得傅里叶级数中各系数的表达式，只要这些积分都存在，那么⑥式等号右侧所表示的傅里叶级数就能用来表达原函数f(t)。上述过程就是整个傅里叶级数的推导过程。事实上，如果能够写出⑥式，不难求出各个系数的表达式，关键是人们不会想到一个周期函数竟然可以用一些简单的正弦或余弦函数来表达，且这个表达式是一个无穷级数。这当然就是数学家傅里叶的天才之作了，我等只有拼命理解的份了。
综上，傅里叶级数的产生过程可以分为以下三步：
1、设想可以把一个周期函数f(t)通过最简单的一系列正弦函数来表示，即5式;
2、通过变形后用三角级数(含sin和cos)来表示;
3、通过积分，把各未知系数用f(t)的积分式来表达;
4、最后得到的4个表达式就是傅里叶级数公式。
在电子学中，傅里叶级数是一种频域分析工具，可以理解成一种复杂的周期波分解成直流项、基波(角频率为ω)和各次谐波(角频率为nω)的和，也就是级数中的各项。一般，随着n的增大，各次谐波的能量逐渐衰减，所以一般从级数中取前n项之和就可以很好接近原周期波形。这是傅里叶级数在电子学分析中的重要应用。
-
傅里叶
+关注
关注
0文章
59浏览量
20464 -
傅里叶变换
+关注
关注
6文章
441浏览量
42590
原文标题：傅里叶级数的数学推导，小白免看！
文章出处：【微信号：EngicoolArabic，微信公众号：电子工程技术】欢迎添加关注！文章转载请注明出处。
发布评论请先 登录
相关推荐
傅里叶级数
详细解释一下傅里叶级数的数学推导过程
傅里叶级数的数学推导
工商网监
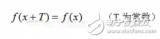
评论