模拟信号与数字信号

vwin 信号与数字信号

一、模拟信号

　　模拟信号是一种不仅再时间上连续、数值上也连续的物理量，具有无穷多的数值，其数学表达是必较复杂，比如正弦函数、指数函数等。
　　从自然界感知的大部分物理量都是模拟性质的，如速度、压力、温度、声音、重量以及位置等都是最常见的物理量。
　　图1.1.1 是几种常见的模拟信号波形

　　正弦波：例如我们最经常接触到的声波。可能你有机会用一台示波器察看一个真实的声音波形，你将发现所看到的波形可不像这里所示范的这样清晰的正弦波，而是看起来非常杂乱的一种波形，确实如此，这只是因为真实的声音波形中包含了多种频率的正弦波。另一个例子由发条驱动的钟摆，将钟摆的运动轨迹延时间轴展开，得到的连续波形正好就是一个正弦波形。
　　调幅波：自从发明收音机以来，普通百姓就开始与调幅波打交道了，这种波形是以一种频率很高的正弦波作为载波，在此基础上叠加一个频率较低的信号波就形成了入图所示得波形。
阻尼振荡波：凡是自然界中可以看到的振荡运动，都可以观察到这种波形，比如弹簧的自由振动、钟摆的自由运动（不同于由发条驱动得钟摆运动）等，如果说这些还有人工的痕迹，那么水波的涟漪则是在自然不过的了。
　　指数衰减波：许多发光物质都具有这种波形，也就是荧光寿命。我们平时使用的日光灯就是一个例子，当我们将一个点亮的日光灯的电源切断时，可以观察到日光灯不是一下子就熄灭，而是有一个短暂的熄灭过程，也就是通常所说的日光灯的余辉。
　　在电子技术中通常采用一些传感器将这些信号转换为电流、电压或电阻等电学量。这些同样是模拟量，因为如果采用一台示波器来测量这些电学量的波形的话，将观察到与图1.1.2图示波形一样的波形。
　　实际使用中电流和电压常用图形来表示。
　　下面我们看到的就是一个幅值为0～5V、周期为100ms的电压波形：

图1.1.2 周期性电压波形

　　图中电压的幅值按照正弦波形周期性地变化，图中显示了两个完整的波形，起始相位为零，如果想确定其中值的个数是不可能的，其值的个数有无穷多个。
　　正如我们在模拟电路中所学习的，周期性模拟信号的基本参数之一是频率，也可以用周期表示。通常频率用f表示，单位为赫兹（Hz）
；周期用T表示，单位为秒（s）。二者之间的关系是互为倒数，即有。图1.1.2中已知电压波形的周期Ｔ＝100ms，则频率为10Hz，该电压的幅值介于0～5V之间，值的个数为无穷大。
　　典型的模拟信号包括工频信号、射频信号、视频信号等。我国和欧洲的工频信号的频率为50Hz ，美国为60Hz 。调幅波的射频信号在 530Hz～1600kHz之间。调频波的射频信号在880MHz～108MHz之间。甚高频（VHF）和超高频（UHF）视频信号在6GHz以上。

二、数字信号

　　电子系统中一般含有模拟和数字两种构件，通常使用的收音机等
，其中的电路结构主要是模拟电路，比如功率放大器，不过现在有许多音响系统中不仅包含模拟电路，而且已经有了数字模块，比如CD机
，其中主要的部件就是数字模块；而像电脑这样一类的电子系统，则主要就是建立在数字技术上的，但即使是所谓的纯数字系统，仍然离不开模拟电路，因为数字电路实事上可以说是模拟电路的一种特例，比如说在模拟电路中我们采用晶体管的线性工作区间，而数字电路则采用晶体管的非线性工作区间，因此说模拟电路是电子系统中必须的组成部分。
　　人们发现在对信号的存储、分析和传输中，数字电路更具优越性
。为了能够处理存储连续变化的模拟信号，数字电路采用二进制数首先对其进行量化处理后，再使用复杂的数字系统来实现信号的存储、分析和量化。

1.二值数字逻辑和逻辑电平

　　二进制数正好是利用二值数字逻辑中的０和１来表示的。二值数字逻辑是Binary DigitalLogic的译称。
　　与模拟信号相反，数字数字信号在时间上和数值上均是离散的，而离散信号的值只有真或假，是与不是，因此可以使用二进制数中的０和１来表示。需要注意的是这里的０和１并非通常意义上的０和１
，也就是说并不像在十进制中０和１有大小之分，这里的０和１指的是逻辑０和逻辑１。
　　因此我们可以将其称之为二值数字逻辑或简称为数字逻辑。
　　二值数字的产生，是基于客观世界中存在许多可以用彼此相关又互相对立的两种状态来描述的事物，比如人的性别，不是男的就是女的，开关的开与关等，就是这样一种关系。很显然，这些都具有明显的二值特性，因此完全可以用电子器件的开关特性来表示。比如，利用晶体管的非线性特性制作成的开关二极管，工作时仅有两种状态，不是导通就是关断，也是一个二值特性，因此可以用其来表示人的性别等。
　　当开关器件起作用时，电路中只可能出现两种电压值，当开关器件导通时，开关后的电路中将有电流流过（比如串联于三极管发射极的负载），因而将可得到一个较高的电压值，而当开关器件关断时，开关后的电路中将没有电流流过，因而将只能得到一个较低的电压值
，从而在电路中将形成离散的电压信号，也叫数字电压，通常称之为逻辑电平。
　　应该注意的是逻辑电平不是一个具体的物理量，而是物理量的相对表示。比如，当使用示波器测量一个音响设备的输出时，你可观察到一个输出电压幅值连续变化的波形，但是将该输出信号量化成二值信号后，你观察到的只是一系列电压值不是５Ｖ就是０Ｖ的离散电压值，很显然我们不能因此就说该音响设备的输出就是５Ｖ。

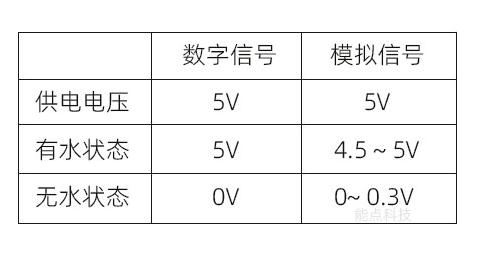
表1.1.1 逻辑电平与电压值的关系

　　从表中可以看到，+5V的电压值可以用二值逻辑中的1或0来表示，就看你使用的是正逻辑还是负逻辑。在逻辑电平中则使用高电平来表示。事实上高电平并非就只等于+5V，可以是3V，还可以是其它任何值。
　　图1.1.3表示用逻辑电平描述的数字波形，其中图1.1.3a的逻辑0表示0V，逻辑1表示5V；图1.1.3b的逻辑0表示5V，逻辑1表示0V；图1.1.3c 则是一个16位长数据的图形表示。

2.数字波形

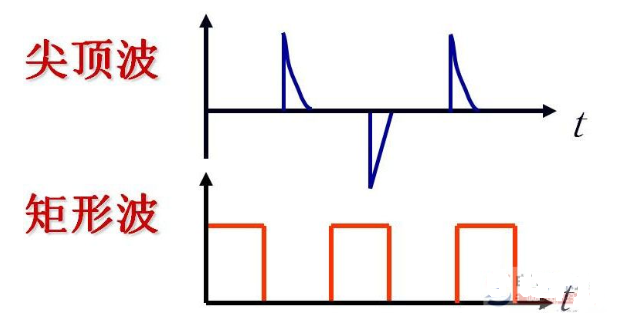
　　数字波形是逻辑电平对时间的图形表示。通常，我们将只有两个离散值的波形称之为脉冲波形，在这一点上脉冲波形与数字波形是一致的，只不过数字波形用逻辑电平表示，而脉冲波形用电压值表示而已。
　　与模拟波形的定义相同，数字波形也有周期性和非周期性之分。图1.1.4表示了这两类数字波形：

　　周期性数字波形同样用周期T或频率f来描述；而脉冲波形的频率常称为脉冲重复率PRR--Pulse Repetition Rate。
　　脉冲波形的参数：
　　脉冲宽度：t_w表示，表示脉冲作用的时间；
　　占空比：q，表示脉冲宽度t_w占整个周期T的百分数，常用下式来表示：
　　占空比是一个重要参数，其定义同样适用于数字波形。
　　图1.1.5表示两种数字波形及其周期、频率、脉冲宽度和占空比：

　　例题1.1.1设周期性数字波形的高电平持续6ms，低电平持续10ms
，求占空比q？

解：根据给定的高电平持续时间有t_w= 6ms，而高电平与低电平持续时间之和即为周期T

　　所以有Ｔ＝6ms＋10ms＝16ms

　　到目前为止，我们所讨论的数字波形都是理想波形，然而实际的数字系统中，数字波形的升降都要经历一段时间，也就是说波形存在上升时间t_r和下降时间t_f。
　　上升时间t_r的定义是：从脉冲幅值的10%到90%所经历的时间；下降时间t_f的定义刚好相反：从脉冲幅值的90%到10%所经历的时间。t_r和t_f的典型值约为几个纳秒（ns），视不同类型的器件和电路而异。
　　脉冲宽度的定义是脉冲幅值为50%时前后两个时间点所跨越的时间。非理想脉冲如图1.1.6所示：

　　例题1.1.2 试绘出一脉冲波形，设它的占空比为50%，脉冲宽度 t_w＝100ns，上升时间t_r＝10ns，下降时间t_f＝20ns。

解：根据题意，可绘出脉冲波形如下：

图1.1.7 例1.1.2的波形图

　　一般情况下波形的上升或下降时间均要比高电平或低电平的持续时间要小很多，画波形的目的主要是为了了解高、低电平所经历的时间。因此在理想波形中就只有高、低电平，而忽略了上升和下降时间
。本课程中所用的数字波形将采用理想波形。
　　当然，实际中碰到的波形，不管从示波器上来看，其上升沿和下降沿是多么的直，t_r和t_f都不可能为零，只是在数字电路中，只需关注逻辑电平的高低，因此在画波形时只需画出高低电平所经历的时间即可，无需画出上升沿和下降沿。

(a)

(b)

图1.1.8 用逻辑1和0表示的二值位行图
(a) 对称方波 (b) 二值数据

　　上图为一个二值位形图，其中１或１占用的最小时间称为位时间
，也就是１位数据所占用的时间。我们将每秒钟所传输的位数称为数据率或比特率。
　　例题1.1.3 某通信系统每秒中传输1.544兆位数据，求每位数据的时间。

解：根据题意，只需将1.544M倒数，即可求得每位数据的时间为：

　　举例来说，象图1.1.8b中看到的22位的二值位形图，如果每一位数据所占用的时间是648ns，则22位共占用14256ns，也就是14.256微秒，而其数据率就是1.544兆。
　　在设计数字集成电路时，有时为了分析各种信号之间的逻辑关系
，需要将多个数字波形按时间排列在一起，用来表明相互间的时间关系，我们将这样一种关系图称为时序图（Timing diagram）。
　　时序图中的每一个波形都被称为时间信号。时序图被广泛运用在设计数字集成电路中，在设计存储器、微处理机等数字应用电路时均须附有时序图，以便数字系统的分析、应用和设计。
　　图1.1.9就是一个时序图的例子：

图1.1.9 数字时序图

　　图中CP为时钟脉冲信号，用作系统中的时间参考信号，一般由石英晶体振荡器来产生，如图所示波形为对称方波。关于图中各个波形的具体作用，将在以后的课程加以介绍

3.模拟量的数字表示

　　为便于存储、分析和传输，常常需要将模拟信号转换为数字信号
。
　　在数字电路中用数字0、1的编码来表示一个模拟量，这里的编码所指的是数字0、1的字符串，图1.1.3和图1.1.8所示的数字波形即是这种编码的图形。这样一种编码实际上就是二进制编码。
　　下面通过图1.1.10的图示来了解用数字表示模拟信号的过程：

　　取其中Ａ、Ｂ、Ｃ３个取样点。以Ｂ点为例，该点的模拟电压为3V，将其送入一个模数转换器后可得到以数字０、１表示的数字电压
，如图1.1.10b所示。同样地也可以得到Ａ、Ｃ点的数字编码。
　　当信号的取样点数足够多时，原信号就可以被较真实地复制下来
。
　　当然，必要的话还可以通过数模转换器将已经数字化的信号还原成模拟信号。