卡诺图的构成及其简法
一 卡诺图的构成
卡诺图是一种平面方格图,每个小方格代表一个最小项,故又称为最小项方格图。
1.结构特点
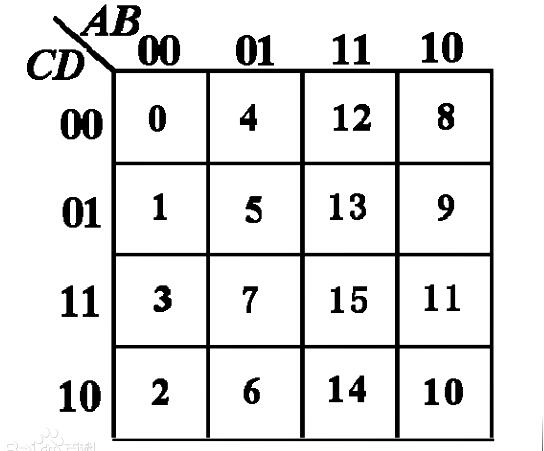
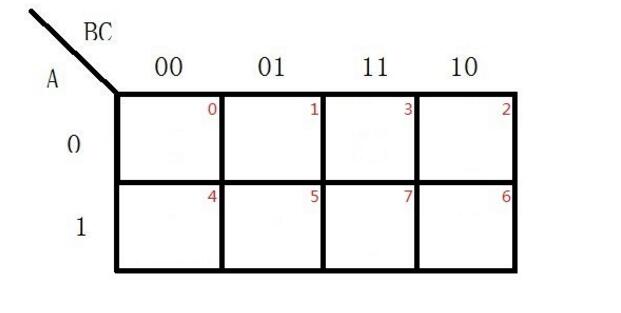
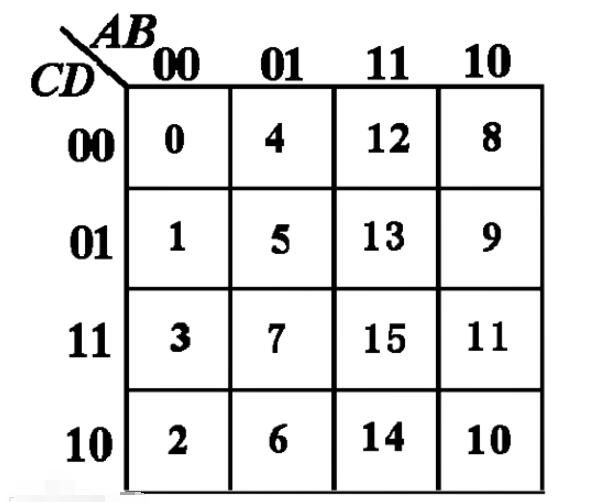
卡诺图中最小项的排列方案不是唯一的,图2.5(a)、(b)、(c)、(d)分别为2变量、3变量、4变量、5变量卡诺图的一种排列方案。图中,变量的坐标值0表示相应变量的反变量,1表示相应变量的原变量。各小方格依变量顺序取坐标值,所得二进制数对应的十进制数即相应最小项的下标i。
在五变量卡诺图中,为了方便省略了符号“m”,直接标出m的下标i 。
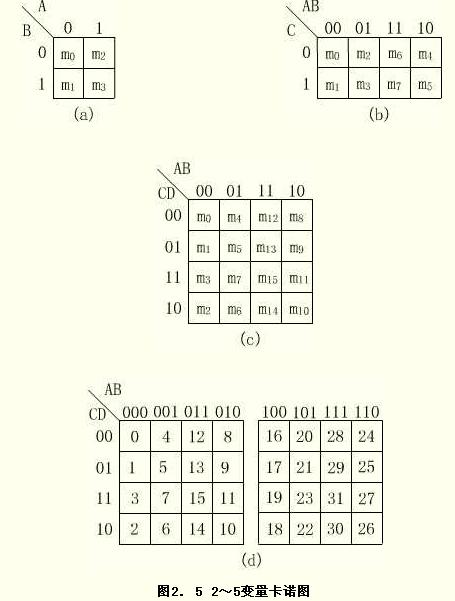
从图2.5所示的各卡诺图可以看出,卡诺图上变量的排列规律使最小项的相邻关系能在图形上清晰地反映出来。具体地说,在n个变量的卡诺图中,能从图形上直观、方便地找到每个最小项的n个相邻最小项。以四变量卡诺图为例,图中每个最小项应有4个相邻最小项,如m5的4个相邻最小项分别是m1,m4,m7,m13,这4个最小项对应的小方格与m5对应的小方格分别相连,也就是说在几何位置上是相邻的,这种相邻称为几何相邻。而m2则不完全相同,它的4个相邻最小项除了与之几何相邻的m3和m6之外,另外两个是处在“相对”位置的m0(同一列的两端)和m10(同一行的两端)。这种相邻似乎不太直观,但只要把这个图的上、下边缘连接,卷成圆筒状,便可看出m0和m2在几何位置上是相邻的。同样,把图的左、右边缘连接,便可使m2和m10相邻。通常把这种相邻称为相对相邻。除此之外,还有“相重”位置的最小项相邻,如五变量卡诺图中的m3,除了几何相邻的m1,m2,m7和相对相邻的m11外,还与m19相邻。对于这种情形,可以把卡诺图左边的矩形重叠到右边矩形之上来看,凡上下重叠的最小项相邻,这种相邻称为重叠相邻。??
归纳起来,卡诺图在构造上具有以下两个特点:
☆ n个变量的卡诺图由2n个小方格组成,每个小方格代表一个最小项;
☆ 卡诺图上处在相邻、相对、相重位置的小方格所代表的最小项为相邻最小项。
二 卡诺图的性质
卡诺图的构造特点使卡诺图具有一个重要性质:可以从图形上直观地找出相邻最小项合并。合并的理论依据是并项定理AB+AB=A。例如,
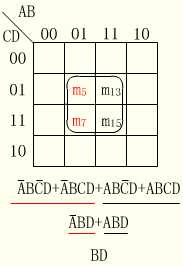
根据定理AB+AB=A和相邻最小项的定义,两个相邻最小项可以合并为一个与项并消去一个变量。例如,4变量最小项ABCD和ABCD相邻,可以合并为ABD;ABCD和ABCD相邻,可以合并为ABD;而与项ABD和ABD又为相邻与项,故按同样道理可进一步将两个相邻与项合并为BD。
用卡诺图化简逻辑函数的基本原理就是把上述逻辑依据和图形特征结合起来,通过把卡诺图上表征相邻最小项的相邻小方格“圈”在一起进行合并,达到用一个简单“与”项代替若干最小项的目的。
通常把用来包围那些能由一个简单“与”项代替的若干最小项的“圈”称为卡诺圈。
三 逻辑函数在卡诺图上的表示??
1.给定逻辑函数为标准“与-或”表达式
当逻辑函数为标准“与-或”表达式时,只需在卡诺图上找出和表达式中最小项对应的小方格填上1,其余小方格填上0,即可得到该函数的卡诺图。??
例如,3变量函数F(A,B,C)=∑m(1,2,3,7)的卡诺图如图2.6所示。
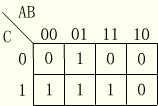
图2.6 函数F(A,B,C)=∑m(1,2,3,7)的卡诺图
2.逻辑函数为一般“与-或”表达式
当逻辑函数为一般“与-或”表达式时,可根据“与”的公共性和“或”的叠加性作出相应卡诺图。
例如,4变量函数F(A,B,C,D)=AB+CD+A·BC的卡诺图如图2.7所示。
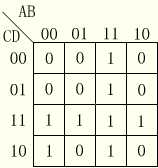
图2.7 函数F(A,B,C,D)=AB+CD+A·BC的卡诺图
填写该函数卡诺图时,只需在4变量卡诺图上依次找出和“与项”AB、CD、A·BC对应的小方格填上1,便可得到该函数的卡诺图。
当逻辑函数表达式为其他形式时,可将其变换成上述形式后再作卡诺图。
为了叙述的方便,通常将卡诺图上填1的小方格称为1方格,填0的小方格称为0方格。0方格有时用空格表示。
四 卡诺图上最小项的合并规律
卡诺图的一个重要特征是,它从图形上直观、清晰地反映了最小项的相邻关系。当一个函数用卡诺图表示后,究竟哪些最小项可以合并呢?下面以2、3、4变量卡诺图为例予以说明。
1.两个小方格相邻, 或处于某行(列)两端时,所代表的最小项可以合并,合并后可消去一个变量。
例如,图2.8给出了2、3、4变量卡诺图上两个相邻最小项合并的典型情况的。

图2.8 两个相邻最小项合并的情况
2.四个小方格组成一个大方格、或组成一行(列)、或处于相邻两行(列)的两端、或处于四角时,所的表的最小项可以合并,合并后可消去两个变量。
例如,图2.9给出了3、4变量卡诺图上四个相邻最小项合并的典型情况的。
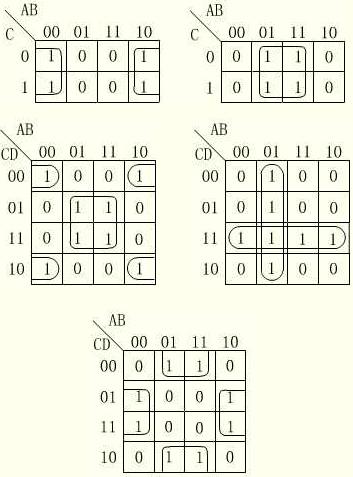
图2.9 四个相邻最小项合并的情况
3.八个小方格组成一个大方格、或组成相邻的两行(列)、或处于两个边行(列)时,所代表的最小项可以合并,合并后可消去三个变量。
例如,图2.10给出了3、4变量卡诺图上八个相邻最小项合并的典型情况的。

图2.10 八个相邻最小项合并的情况
至此,以3、4变量卡诺图为例,讨论了2,4,8个最小项的合并方法。依此类推,不难得出n个变量卡诺图中最小项的合并规律。
归纳起来,n个变量卡诺图中最小项的合并规律如下:
(1)卡诺圈中小方格的个数必须为2m个,m为小于或等于n的整数。
(2)卡诺圈中的2m个小方格有一定的排列规律,具体地说,它们含有m个不同变量,(n-m)个相同变量。
(3)卡诺圈中的2m个小方格对应的最小项可用(n-m)个变量的“与”项表示,该“与”项由这些最小项中的相同变量构成。
(4)当m=n时,卡诺圈包围了整个卡诺图,可用1表示,即n个变量的全部最小项之和为1。
五、卡诺图化简逻辑函数
1.几个定义
蕴涵项:在函数的“与-或”表达式中,每个“与”项被称为该函数的蕴涵项(Implicant)。
显然,在函数卡诺图中,任何一个1方格所对应的最小项或者卡诺圈中的2m个1方格所对应的“与”项都是函数的蕴涵项。
质蕴涵项:若函数的一个蕴涵项不是该函数中其他蕴涵项的子集,则此蕴涵项称为质蕴涵项(Prime Implicant),简称为质项。
显然,在函数卡诺图中,按照最小项合并规律,如果某个卡诺圈不可能被其他更大的卡诺圈包含,那么,该卡诺圈所对应的“与”项为质蕴涵项。
必要质蕴涵项:若函数的一个质蕴涵项包含有不被函数的其他任何质蕴涵项所包含的最小项,则此质蕴涵项被称为必要质蕴涵项(Essential Prime Implicant),简称为必要质项。
在函数卡诺图中,若某个卡诺圈包含了不可能被任何其他卡诺圈包含的1方格,那么,该卡诺圈所对应的“与”项为必要质蕴涵项。
2.求函数最简“与-或”表达式
(1)一般步骤:
第一步:作出函数的卡诺图。
第二步:在卡诺图上圈出函数的全部质蕴涵项。按照卡诺图上最小项的合并规律,对函数F卡诺图中的1方格画卡诺圈。为了圈出全部质蕴涵项,画卡诺圈时在满足合并规律的前题下应尽可能大,若卡诺圈不可能被更大的卡诺圈包围,则对应的“与”项为质蕴涵项。
第三步:从全部质蕴涵项中找出所有必要质蕴涵项。在卡诺图上只被一个卡诺圈包围的最小项被称为必要最小项,包含必要最小项的质蕴涵项即必要质蕴涵项。为了保证所得结果无一遗漏地覆盖函数的所有最小项,函数表达式中必须包含所有必要质蕴涵项。
第四步:求出函数的最简质蕴涵项集。若函数的所有必要质蕴涵项尚不能覆盖卡诺图上的所有1方格,则从剩余质蕴涵项中找出最简的所需质蕴涵项,使它和必要质蕴涵项一起构成函数的最小覆盖。
归纳起来,卡诺图化简的原则是:
☆ 在覆盖函数中的所有最小项的前提下,卡诺圈的个数达到最少。
☆ 在满足合并规律的前题下卡诺圈应尽可能大。
☆ 根据合并的需要,每个最小项可以被多个卡诺圈包围。
3.求函数的最简“或-与”表达式
当需要求一个函数的最简“或-与”表达式时,可采用“两次取反法”。
具体如下:
☆ 先求出函数F的反函数F的最简“与-或”表达(合并卡诺图上的0方格);
☆ 然后对F的最简“与-或”表达式取反,从而得到函数F的最简“或-与”表达式。
例如, 用卡诺图求逻辑函数F(A,B,C,D)=∑m(3,4,6,7,11,12,13,14,15)的最简“或-与”表达式。
解 首先画出函数F的卡诺图如图2.13所示。
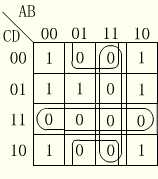
图2.13
图中,F的0方格即反函数F的1方格,它们代表F的各个最小项,将全部0方格合并就可得到反函数F的最简“与-或”表达式
F(A,B,C,D)=AB+CD+BD
再对上述函数式两边取反,即可求得函数的最简“或-与”表达式
卡诺图化简逻辑函数具有方便、直观、容易掌握等优点。但依然带有试凑性。尤其当变量个数大于6时,画图以及对图形的识别都变得相当复杂。
为了克服它的不足,引入了另一种化简方法--列表化简法。
卡诺图是一种平面方格图,每个小方格代表一个最小项,故又称为最小项方格图。
1.结构特点
卡诺图中最小项的排列方案不是唯一的,图2.5(a)、(b)、(c)、(d)分别为2变量、3变量、4变量、5变量卡诺图的一种排列方案。图中,变量的坐标值0表示相应变量的反变量,1表示相应变量的原变量。各小方格依变量顺序取坐标值,所得二进制数对应的十进制数即相应最小项的下标i。
在五变量卡诺图中,为了方便省略了符号“m”,直接标出m的下标i 。

从图2.5所示的各卡诺图可以看出,卡诺图上变量的排列规律使最小项的相邻关系能在图形上清晰地反映出来。具体地说,在n个变量的卡诺图中,能从图形上直观、方便地找到每个最小项的n个相邻最小项。以四变量卡诺图为例,图中每个最小项应有4个相邻最小项,如m5的4个相邻最小项分别是m1,m4,m7,m13,这4个最小项对应的小方格与m5对应的小方格分别相连,也就是说在几何位置上是相邻的,这种相邻称为几何相邻。而m2则不完全相同,它的4个相邻最小项除了与之几何相邻的m3和m6之外,另外两个是处在“相对”位置的m0(同一列的两端)和m10(同一行的两端)。这种相邻似乎不太直观,但只要把这个图的上、下边缘连接,卷成圆筒状,便可看出m0和m2在几何位置上是相邻的。同样,把图的左、右边缘连接,便可使m2和m10相邻。通常把这种相邻称为相对相邻。除此之外,还有“相重”位置的最小项相邻,如五变量卡诺图中的m3,除了几何相邻的m1,m2,m7和相对相邻的m11外,还与m19相邻。对于这种情形,可以把卡诺图左边的矩形重叠到右边矩形之上来看,凡上下重叠的最小项相邻,这种相邻称为重叠相邻。??
归纳起来,卡诺图在构造上具有以下两个特点:
☆ n个变量的卡诺图由2n个小方格组成,每个小方格代表一个最小项;
☆ 卡诺图上处在相邻、相对、相重位置的小方格所代表的最小项为相邻最小项。
二 卡诺图的性质
卡诺图的构造特点使卡诺图具有一个重要性质:可以从图形上直观地找出相邻最小项合并。合并的理论依据是并项定理AB+AB=A。例如,

根据定理AB+AB=A和相邻最小项的定义,两个相邻最小项可以合并为一个与项并消去一个变量。例如,4变量最小项ABCD和ABCD相邻,可以合并为ABD;ABCD和ABCD相邻,可以合并为ABD;而与项ABD和ABD又为相邻与项,故按同样道理可进一步将两个相邻与项合并为BD。
用卡诺图化简逻辑函数的基本原理就是把上述逻辑依据和图形特征结合起来,通过把卡诺图上表征相邻最小项的相邻小方格“圈”在一起进行合并,达到用一个简单“与”项代替若干最小项的目的。
通常把用来包围那些能由一个简单“与”项代替的若干最小项的“圈”称为卡诺圈。
三 逻辑函数在卡诺图上的表示??
1.给定逻辑函数为标准“与-或”表达式
当逻辑函数为标准“与-或”表达式时,只需在卡诺图上找出和表达式中最小项对应的小方格填上1,其余小方格填上0,即可得到该函数的卡诺图。??
例如,3变量函数F(A,B,C)=∑m(1,2,3,7)的卡诺图如图2.6所示。

图2.6 函数F(A,B,C)=∑m(1,2,3,7)的卡诺图
2.逻辑函数为一般“与-或”表达式
当逻辑函数为一般“与-或”表达式时,可根据“与”的公共性和“或”的叠加性作出相应卡诺图。
例如,4变量函数F(A,B,C,D)=AB+CD+A·BC的卡诺图如图2.7所示。

图2.7 函数F(A,B,C,D)=AB+CD+A·BC的卡诺图
填写该函数卡诺图时,只需在4变量卡诺图上依次找出和“与项”AB、CD、A·BC对应的小方格填上1,便可得到该函数的卡诺图。
当逻辑函数表达式为其他形式时,可将其变换成上述形式后再作卡诺图。
为了叙述的方便,通常将卡诺图上填1的小方格称为1方格,填0的小方格称为0方格。0方格有时用空格表示。
四 卡诺图上最小项的合并规律
卡诺图的一个重要特征是,它从图形上直观、清晰地反映了最小项的相邻关系。当一个函数用卡诺图表示后,究竟哪些最小项可以合并呢?下面以2、3、4变量卡诺图为例予以说明。
1.两个小方格相邻, 或处于某行(列)两端时,所代表的最小项可以合并,合并后可消去一个变量。
例如,图2.8给出了2、3、4变量卡诺图上两个相邻最小项合并的典型情况的。

图2.8 两个相邻最小项合并的情况
2.四个小方格组成一个大方格、或组成一行(列)、或处于相邻两行(列)的两端、或处于四角时,所的表的最小项可以合并,合并后可消去两个变量。
例如,图2.9给出了3、4变量卡诺图上四个相邻最小项合并的典型情况的。

图2.9 四个相邻最小项合并的情况
3.八个小方格组成一个大方格、或组成相邻的两行(列)、或处于两个边行(列)时,所代表的最小项可以合并,合并后可消去三个变量。
例如,图2.10给出了3、4变量卡诺图上八个相邻最小项合并的典型情况的。

图2.10 八个相邻最小项合并的情况
至此,以3、4变量卡诺图为例,讨论了2,4,8个最小项的合并方法。依此类推,不难得出n个变量卡诺图中最小项的合并规律。
归纳起来,n个变量卡诺图中最小项的合并规律如下:
(1)卡诺圈中小方格的个数必须为2m个,m为小于或等于n的整数。
(2)卡诺圈中的2m个小方格有一定的排列规律,具体地说,它们含有m个不同变量,(n-m)个相同变量。
(3)卡诺圈中的2m个小方格对应的最小项可用(n-m)个变量的“与”项表示,该“与”项由这些最小项中的相同变量构成。
(4)当m=n时,卡诺圈包围了整个卡诺图,可用1表示,即n个变量的全部最小项之和为1。
五、卡诺图化简逻辑函数
1.几个定义
蕴涵项:在函数的“与-或”表达式中,每个“与”项被称为该函数的蕴涵项(Implicant)。
显然,在函数卡诺图中,任何一个1方格所对应的最小项或者卡诺圈中的2m个1方格所对应的“与”项都是函数的蕴涵项。
质蕴涵项:若函数的一个蕴涵项不是该函数中其他蕴涵项的子集,则此蕴涵项称为质蕴涵项(Prime Implicant),简称为质项。
显然,在函数卡诺图中,按照最小项合并规律,如果某个卡诺圈不可能被其他更大的卡诺圈包含,那么,该卡诺圈所对应的“与”项为质蕴涵项。
必要质蕴涵项:若函数的一个质蕴涵项包含有不被函数的其他任何质蕴涵项所包含的最小项,则此质蕴涵项被称为必要质蕴涵项(Essential Prime Implicant),简称为必要质项。
在函数卡诺图中,若某个卡诺圈包含了不可能被任何其他卡诺圈包含的1方格,那么,该卡诺圈所对应的“与”项为必要质蕴涵项。
2.求函数最简“与-或”表达式
(1)一般步骤:
第一步:作出函数的卡诺图。
第二步:在卡诺图上圈出函数的全部质蕴涵项。按照卡诺图上最小项的合并规律,对函数F卡诺图中的1方格画卡诺圈。为了圈出全部质蕴涵项,画卡诺圈时在满足合并规律的前题下应尽可能大,若卡诺圈不可能被更大的卡诺圈包围,则对应的“与”项为质蕴涵项。
第三步:从全部质蕴涵项中找出所有必要质蕴涵项。在卡诺图上只被一个卡诺圈包围的最小项被称为必要最小项,包含必要最小项的质蕴涵项即必要质蕴涵项。为了保证所得结果无一遗漏地覆盖函数的所有最小项,函数表达式中必须包含所有必要质蕴涵项。
第四步:求出函数的最简质蕴涵项集。若函数的所有必要质蕴涵项尚不能覆盖卡诺图上的所有1方格,则从剩余质蕴涵项中找出最简的所需质蕴涵项,使它和必要质蕴涵项一起构成函数的最小覆盖。
归纳起来,卡诺图化简的原则是:
☆ 在覆盖函数中的所有最小项的前提下,卡诺圈的个数达到最少。
☆ 在满足合并规律的前题下卡诺圈应尽可能大。
☆ 根据合并的需要,每个最小项可以被多个卡诺圈包围。
3.求函数的最简“或-与”表达式
当需要求一个函数的最简“或-与”表达式时,可采用“两次取反法”。
具体如下:
☆ 先求出函数F的反函数F的最简“与-或”表达(合并卡诺图上的0方格);
☆ 然后对F的最简“与-或”表达式取反,从而得到函数F的最简“或-与”表达式。
例如, 用卡诺图求逻辑函数F(A,B,C,D)=∑m(3,4,6,7,11,12,13,14,15)的最简“或-与”表达式。
解 首先画出函数F的卡诺图如图2.13所示。

图2.13
图中,F的0方格即反函数F的1方格,它们代表F的各个最小项,将全部0方格合并就可得到反函数F的最简“与-或”表达式
F(A,B,C,D)=AB+CD+BD
再对上述函数式两边取反,即可求得函数的最简“或-与”表达式
卡诺图化简逻辑函数具有方便、直观、容易掌握等优点。但依然带有试凑性。尤其当变量个数大于6时,画图以及对图形的识别都变得相当复杂。
为了克服它的不足,引入了另一种化简方法--列表化简法。
 德赢Vwin官网
App
德赢Vwin官网
App



























评论