在数字电路中,卡诺图是用最小项方格表示逻辑函数的方法,其是用图形表示输入变量与函数之间的逻辑关系,它用几何位置上的相邻,形象地表示了组成逻辑函数的各个最小项之间在逻辑上的相邻性。初学者往往以为卡诺图只是数字电路分析和设计中用以化简逻辑函数的一种工具。其实不然,实际上灵活运用卡诺图,可以使逻辑电路的分析和设计过程大大地简化,让一些难题迎刃而解。下面介绍卡诺图在化简之外的几点灵活运用。
1 卡诺图的应用
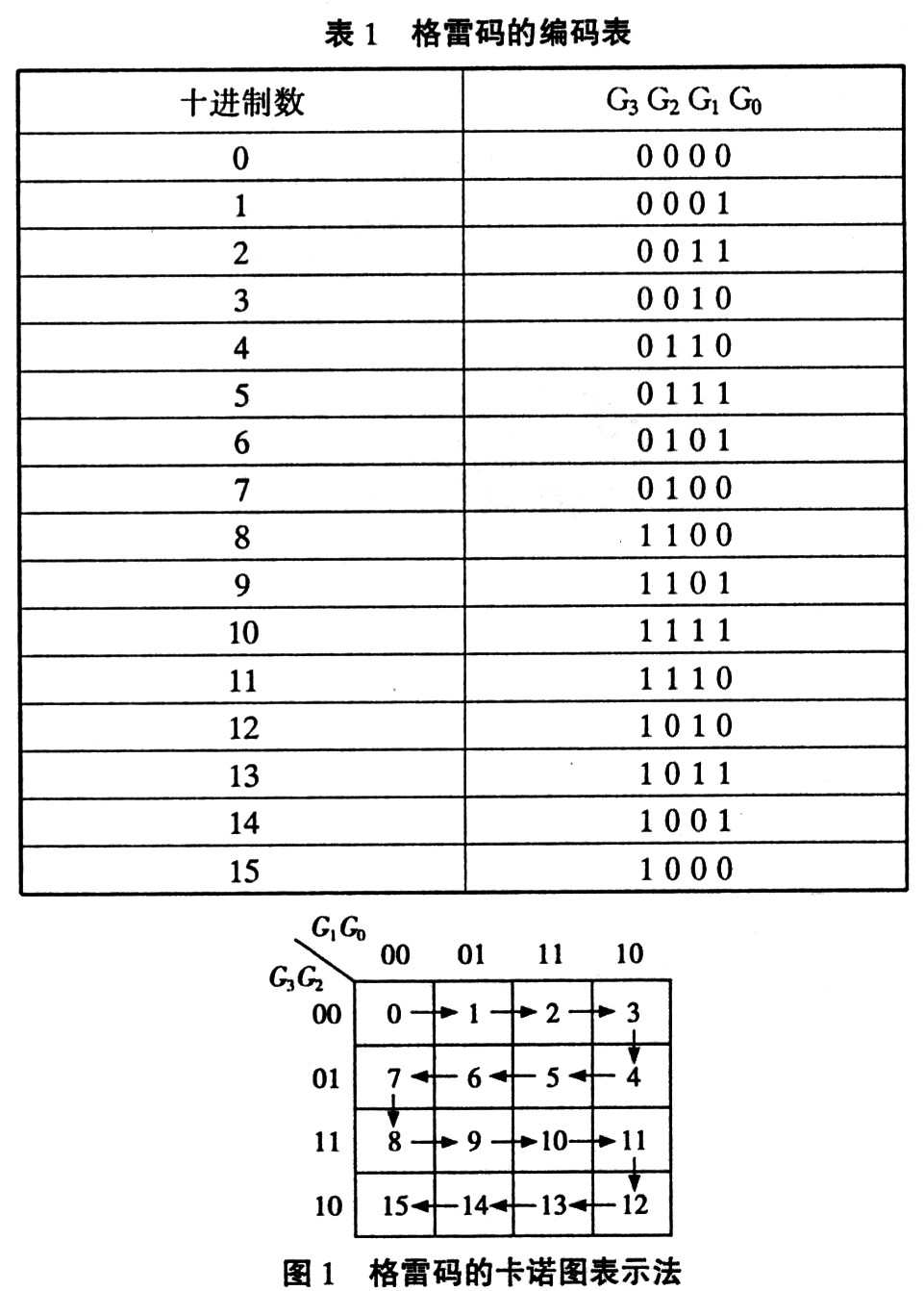
1.1 利用卡诺图结构帮助记忆格雷码
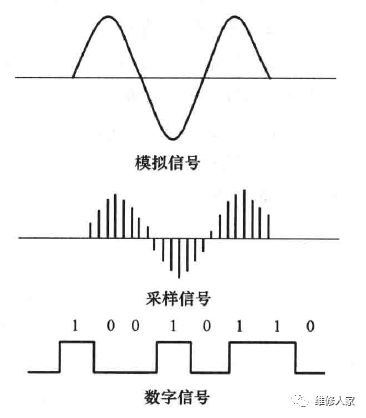
格雷码是一种常用的无权BCD码,相邻两码之间只有一位二进制数码不同。常用于vwin 量的转换中,当模拟量发生微小变化而可能引起数字量发生变化时,格雷码仅改变1位,这样与其他码同时改变两位或多位的情况相比更为可靠,可减少出错的可能性,提高电路的抗干扰能力,它是一种典型的可靠性代码,这种码制在数控装置中有着广泛的应用。但由于这种编码所具有的独特性,实际应用中很难记忆。经研究和探讨,我们观察到利用卡诺图按照一定规律取值,可用于实现记忆格雷码。这种独特的记忆方式,可帮助学生方便、轻松地记住该编码,并应用于实际中。
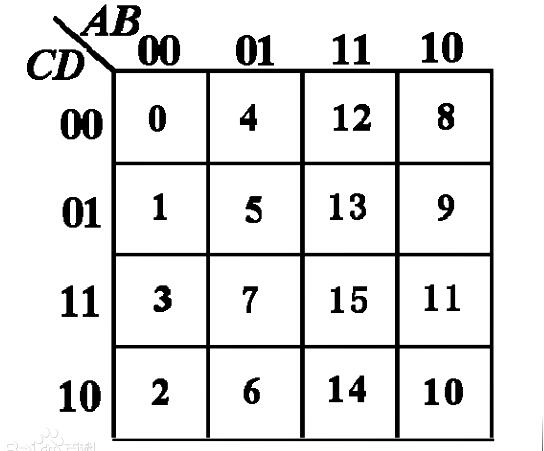
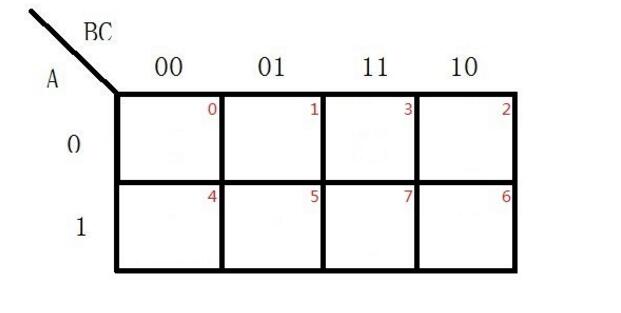
选用四变量卡诺图并令:G3G2G1G0分别作为四位格雷码的输入变量。将变量G3G2作为高位,GlGO作为低位。画出四变量卡诺图。从四变量卡诺图中我们可见,卡诺图中四变量若按箭头所示的方向顺序取值,其所取的值变化顺序正好即为四位格雷码的编码表,如图1格雷码的卡诺图表示法所示。十进制数从 0~15,对应四位格雷码的输入代码依次分别为0000—0001—0011——1001一1000,如表l所示格雷吗码的编码表。
1.2 卡诺图在组合逻辑电路竞争冒险中的应用
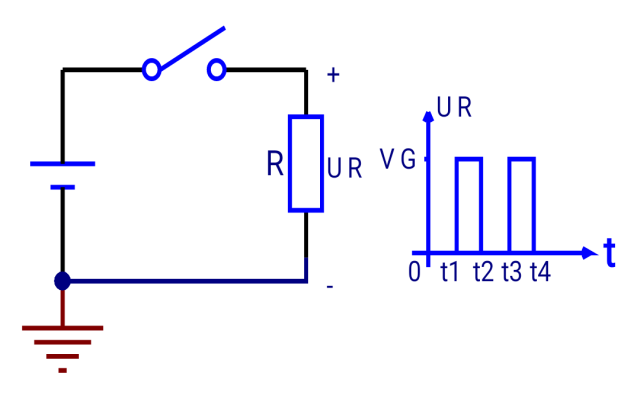
竞争冒险,是数字电路中一种特有的现象。不同的门电路有着不同的延迟时间,输入信号经过不同的途径进行传输,到达输出端的时间有早有迟,状态变化有先有后,存在时差。这种状态变化存在时差的现象就叫做“竞争”。如果竞争结果是使稳态输出的逻辑关系受到短暂破坏,出现不应有的尖峰脉冲,这种现象就叫做“冒险”。冒险可能使电路产生暂时或永久的逻辑错误。
在进行逻辑电路设计时,我们必须应发现和判别出产生竞争冒险的可能,并采取积极有效的措施将竞争冒险予以消除。判断和消除竞争冒险的方法很多,最简便和最直观的方法就是使用卡诺图。
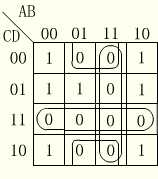
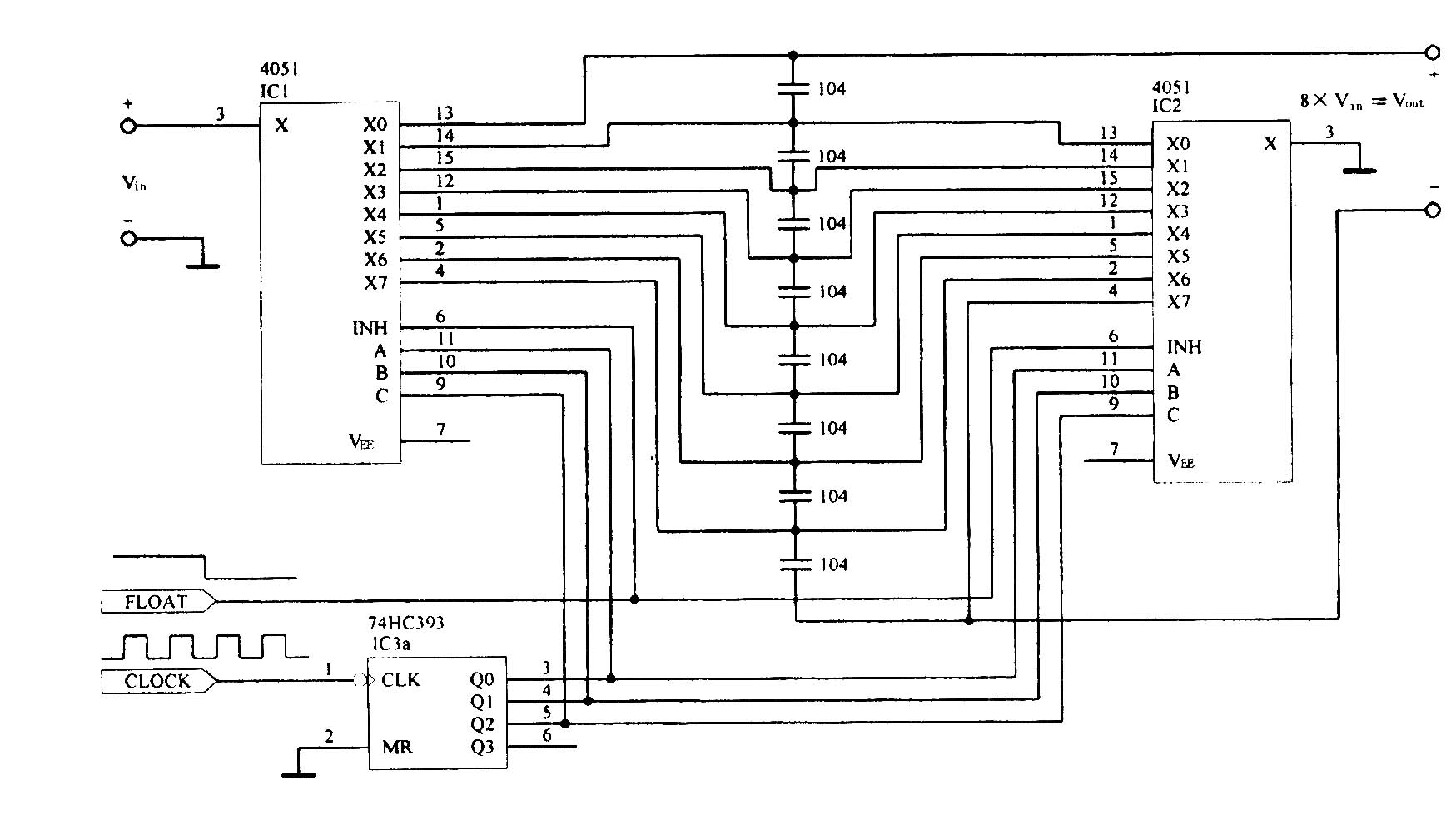
使用卡诺图判断一个组合逻辑电路是否存在着竞争冒险的一般步骤是:首先画出该电路逻辑函数的卡诺图,然后在函数卡诺图上画出与表达式中所有乘积项相对应的卡诺圈,如果图中有相切的卡诺圈,则该逻辑电路存在着竞争冒险如图2所示,所谓卡诺圈相切即两个卡诺圈之间存在不被同一卡诺圈包含的相邻最小项。

如果逻辑函数的卡诺图中存在着相切的卡诺圈,该逻辑电路就存在着竞争冒险;那么,只要使函数的卡诺图中消除相切的卡诺圈,即可消除竞争冒险现象。在卡诺图上,加上一个与两相切卡诺圈相交的一个圈(一项),破坏卡诺圈的单独相切性。加上此圈后,逻辑函数多了一个冗余项,冗余项的加入并不改变原逻辑函数的逻辑值,但冗余项的加入却可以有效地消除冒险。

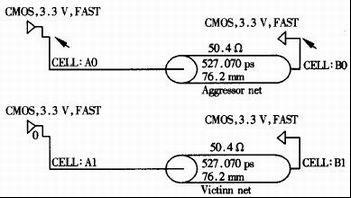
例如图3所示的卡诺图中,有两处存在卡诺圈相切现象,故其表示的逻辑函数式F=ABC十ABD+AD存在冒险。可加两个卡诺圈(虚线圈)破坏其相切性,也即增加两个冗余项BCD和ACD,消除竞争冒险后,该逻辑函数的表达式如下所示:
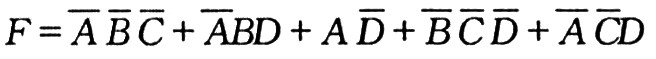
由此可见,使用卡诺图判断和消除数字电路中的竞争冒险,简便直观,易于操作。
1.3 用卡诺图完成两逻辑函数的逻辑运算
首先将逻辑函数F1和F2在同一张卡诺图中表示出来。为区别起见,将函数F1出现的l填在卡诺图小方格的左上角,将另一函数F2出现的l填在卡诺图小方格的左下角。
下面以几个常见的逻辑运算为例来说明。
1)求两逻辑函数Y1和Y2的或运算F1+F2
根据或运算的特点,求或运算时,只要将Y1、Y2卡诺图中出现的所有l都画入包围圈,然后根据卡诺图写出表达式。
2)求两逻辑函数Fl和F2的与运算Fl·F2
根据与运算的特点,求与运算时,只要将F1、F2卡诺图中重复出现的l画入包围圈,然后根据卡诺图写出表达式。
3)求两逻辑函数Fl和F2的异或运算Fl+F2
根据异或运算的特点,求异或运算时,只要将Fl、F2卡诺图中不重复出现的l画入包围,然后根据卡诺图写出表达式。
例:已知两逻辑函数F1(A,B,C)=∑m(0,1,3),F2(A,B,C)=∑m(0,4,5,7),试用卡诺图分别求出F1+F2;Fl·F2和Fl+F2。
解:
1)将逻辑函数Fl、F2在同一张卡诺图中表示出来,将函数出现的1填在卡诺图小方格的左上角,将函数F2出现的l填在卡诺图小方格的左下角,如图4;
2)求Fl+F2时,将Fl、F2卡诺图中出现的所有l都画入包围圈,如图5;
3)求F1·F2时,将F1、F2卡诺图中重复出现的1画入包围圈,如图6;
4)求F1+F2时,将F1、F2卡诺图中不重复出现的1画入包围圈,如图7;
5)根据图5、6、7写出函数表达式:

1.4 使用降维卡诺图化简多变量函数
在卡诺图中,通常我们用“0”、“1”以及无关项“d”(或用“×”表示)作为卡诺图中的单元值,函数的变量都作为卡诺图的变量,一般来说,卡诺图的维数也就是函数的变量数.如果将某些变量也作为图中的单元值,则所得到的卡诺图维数将减少,这样的卡诺图叫做降维卡诺图。在用中规模集成电路,特别是用数据选择器来实现函数时,使用降维卡诺图化简多变量函数是非常有用的。降维卡诺图化简原理在此不再赘述。
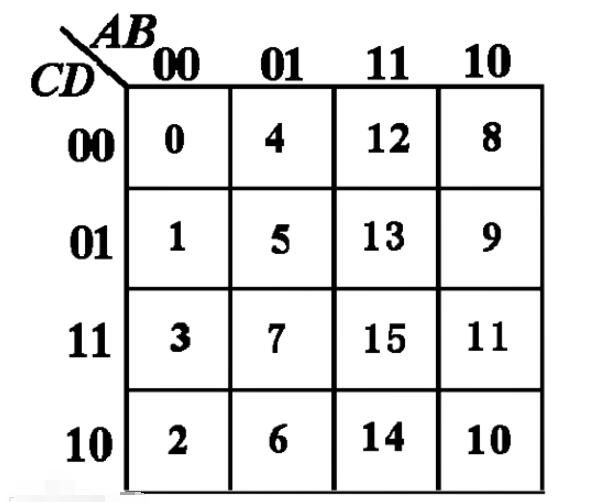
例如逻辑函数F(A,B,C,D)=∑m(0,3,5,6,9,10,12,15) 如果选用8选1数据选择器74LSl5l实现组合逻辑函数,由于8选l数据选择器的地址变量为3个,将逻辑函数降维为三维卡诺图后与8选1数据选择器含 Di的卡诺图对照比较(见图8),很容易获得数据选择器输入信号与逻辑函数变量的关系:令A2=A,A1=B,A0=C,则 Do="D3"=D5=D6=D,Dl=D2=D4=D7=D,画出逻辑图,如图9所示。
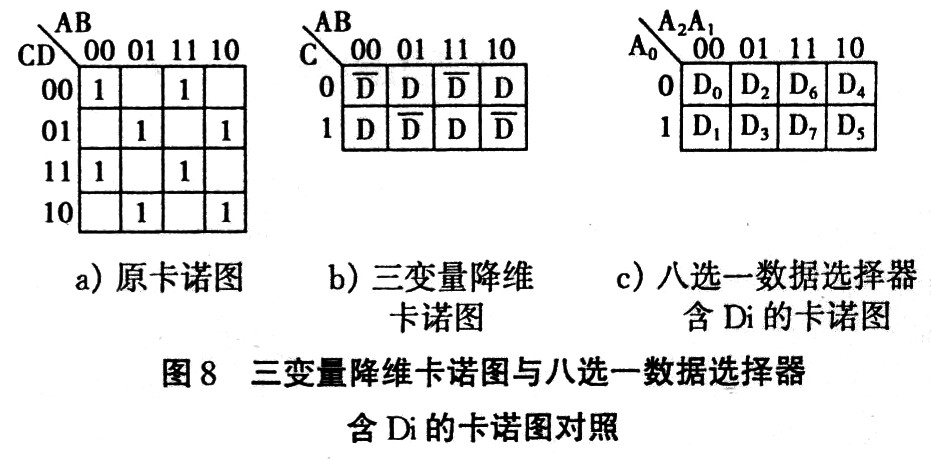
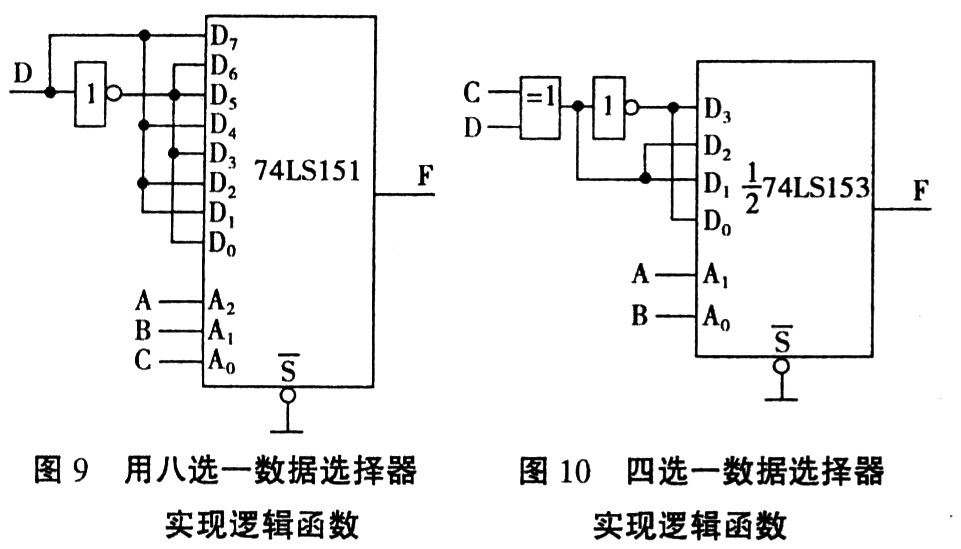
如果选用4选一数据选择器实现逻辑函数,还可以将三维卡诺图继续降维成二维卡诺图后与4选l数据选择器含Di的卡诺图对照比较(见图11),获得数据选择器输入信号与逻辑函数变量的关系:A1=A,A0=B,D0=D3=CD+CD=C+D,Dl=D2=CD+CD=C+D
用4选一数据选择器实现逻辑函数见图10。

2 结束语
从以上几例论述可知,卡诺图的用途不只限于逻辑函数化简的功能,可广泛用于记忆或设计有关码制,竞争冒险中的判断,数据选择器实现组合逻辑函数和逻辑函数的逻辑运算等,深入理解卡诺图的内涵,巧妙地应用它,能得到意想不到的效果,为数字逻辑电路的分析和综合带来很大的方便。
 德赢Vwin官网
App
德赢Vwin官网
App
























评论