德赢Vwin官网
App
比例运算电路的工作原理
比例运算电路的输出电压与输入电压之间存在比例关系，即电路可实现比例运算。比例电路是最基本的运算电路，是其他各种运算电路的基础，本章随后将要介绍的求和电路、积分和微分电路、对数和指数电路等等，都是在比例电路的基础上，加以扩展或演变以后得到的。
比例运算电路的分类
根据输入信号接法的不同，比例电路有三种基本形式：反相输入、同相输入以及差分输入比例电路。
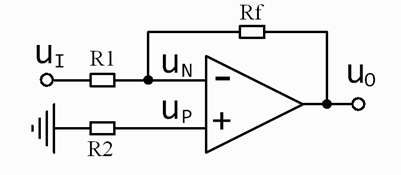
1、反相比例运算电路
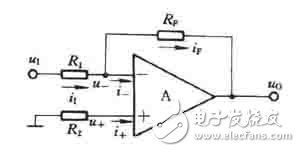
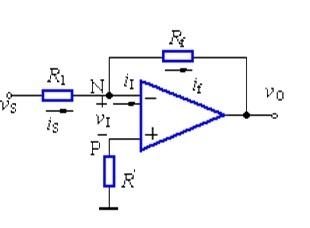
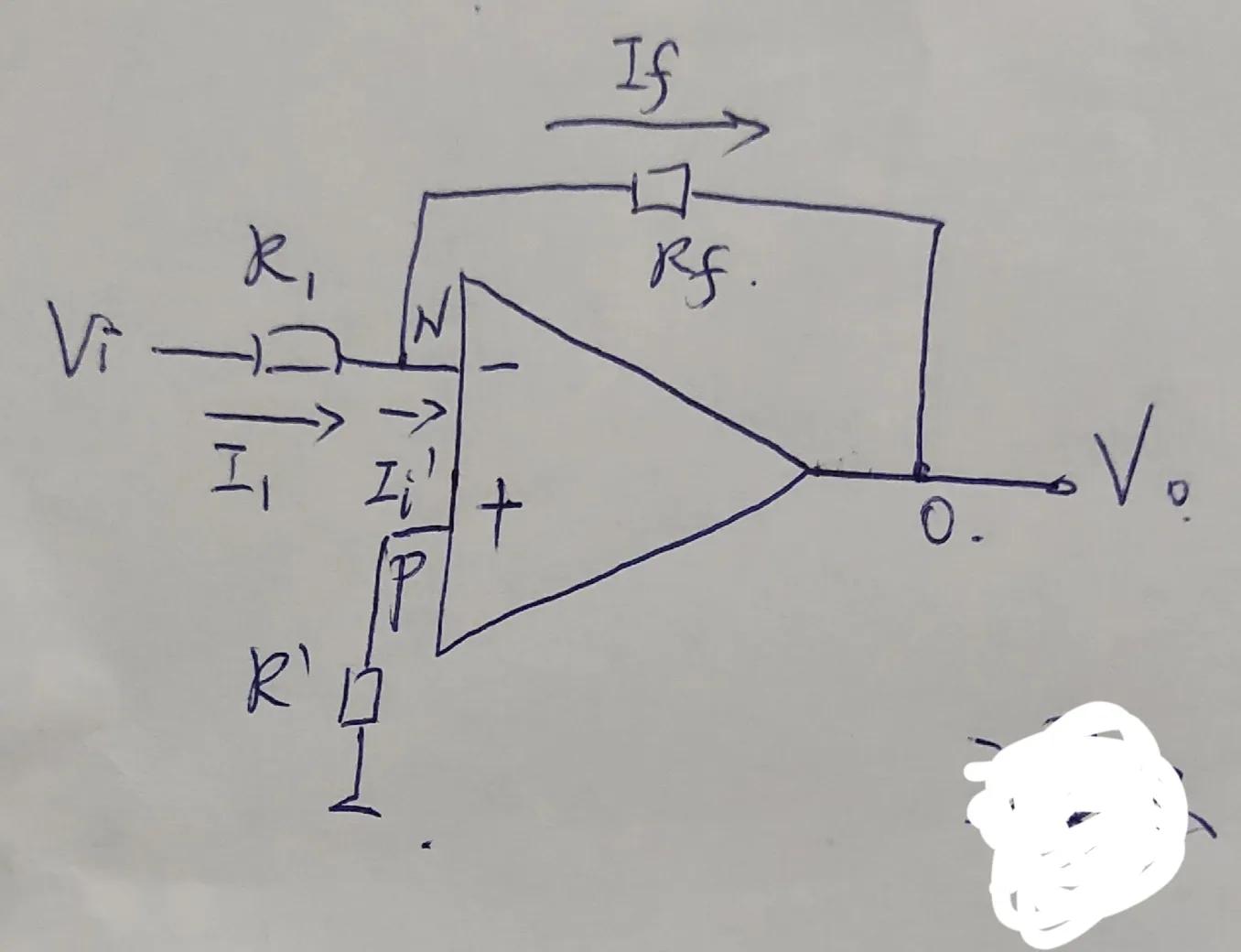
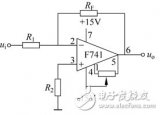
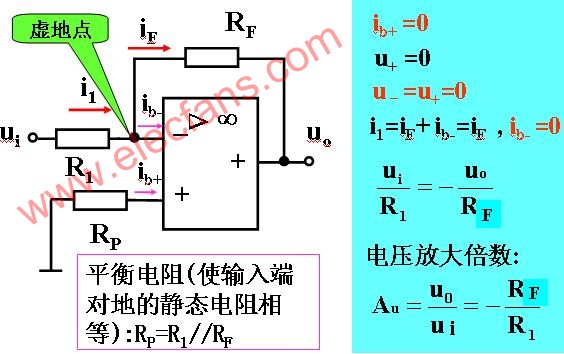
在上图中，输入电压u1经电阻R1加到集成支放的反相输入端，其同相输入端经电阻R2接地。输出电压u0经RF接回到反相输入端。集成运放的反相输入端和同相输入端，实际上是运放内部输入级两个差分对管的基极。为使差动放大电路的参数保持对称，应使两个差分对管基极对地的电阻尽量一致，以免静态基流流过这两个电阻时，在运放输入端产生附加的偏差电压。因此，通常选择R2的阻值为
R2=R1 // RF （1）
经过分析可知，反相比例运算电路中反馈的组态是电压并联负反馈。由于集成运放的开环差模增益很高，因此容易满足深负反馈的条件，故可以认为集成运放工作在线性区。因此，可以利用理想运放工作在线性区时“虚短”和“虚断”的特点来分析反相比例运算电路的电压放大倍数。
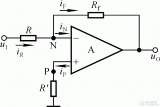
在上图中，由于“虚断”，故i+=0，即R2上没有压降，则u+=0。又因“虚短”，可得
u-= u+=0 （2）
上述说明在反相比例运算电路中，集成运放的反相输入端与同相输入端两点的电位不仅相等，而且均等于零，如同该两点接地一样，这种现象称为“虚地”。“虚地”是反相比例运算电路的一个重要特点。
由于I-=0，由由图可见
iI= iF
即
上式中u-=0，由此可求得反相比例运算电路的电压放大倍数为
（3）
下面分析反相比例运算电路的输入电阻。因为反相输入端“虚地”，显而易见，电路的输入电阻为
Rif = R1 （4）
综合以上分析，对反相比例运算电路可以归纳得出以下几点结论：
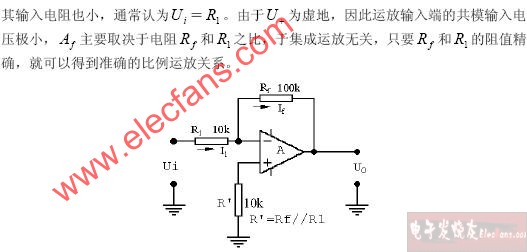
1）反相比例运算电路实际上是一个深度的电压并联负反馈电路。在理想情况下，反相输入端的电位等于零，称为“虚地”。因此加在集成运簇输入端的共模输入电压很小。
2）电压放大倍数
， 即输出电压与输入电压的幅值成正比，但相位
相反。也就是说，电路实现了反相比例运算。比值 Auf 决定于电阻RF和R1之比，而与集成运放内部各项参数无关。只要RF和R1的阻值比较准确而稳定，就可以得到准确的比例运算关系。比值Auf 可以大于1，也可以小于1。当RF=R1时，Auf=-1，称为单位增益倒相器。
3）由于引入了深度电压并联负反馈，因此电路的输入电阻不高，输出电阻很低。
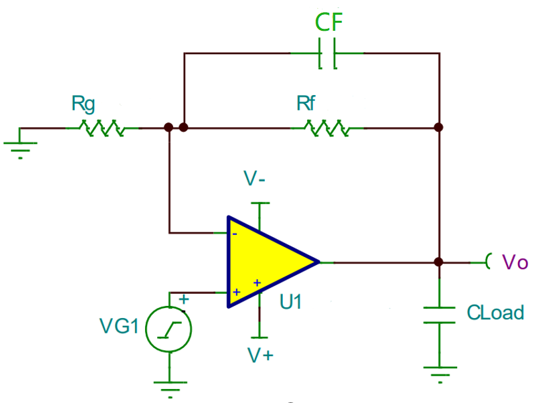
2、同相比例运算电路
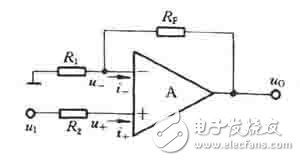
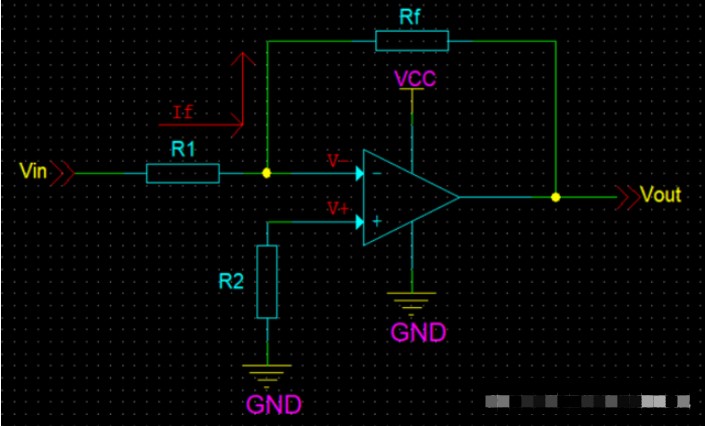
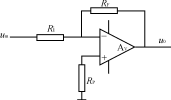
在上图中，输入电压u1接至同相输入端，但是为保证引入的是负反馈，输出电压uo通过电阴RF仍接到反相输入端，同时，反相输入端通过电阴R1接地。为了使集成运放反相输入端和同相输入端对地的电阻一致，R2的阻值仍应为
R2 = R1 // RF
同相比例运算电路中反馈的组态为电压串联负反馈，同样可以利用理想运放工作在线性区时的两个特点来分析其电压放大位数。
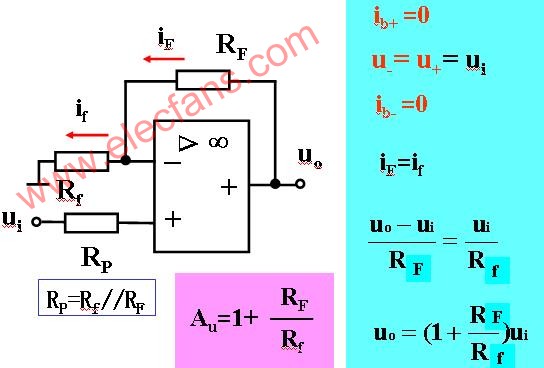
在上图中，根据“虚短”和“虚断”的特点可知， i_=i+=0， 故
则同相比例运算电路的电压放大倍数为
（5）
由于引入了电压串联负反馈，因此能够提高输入电阻，而且提高的程度与反馈深度有关。在理想运放条件下，即认为Aod 趋于无穷大，Rid趋于无穷大 ，则同相比例运算电路的输入电阻Rid 趋于无穷大。当考虑Aod≠ ∞，Rid ≠ ∞的一般情况时，经过分析可知，同相比例运算电路的输入电阻为
Rid = （1 + AodF）Rid （6）
式中Aod和Rid分别是集成运放的开环差模电压增益和差模输入电阻，F是反馈系数，在本电路中
由式（5）可知，同相比例运算电路的电压放大倍数总是大于或等于1。
由于这种电路的输出电压与输入电压不仅幅值相等，而且相位也相同，二者之间是一种“跟随”关系，所以又称为电压跟随器。
综上所述，对同相比例运算电路可以得到以下几点结论：
1）相比例运算放大电路是一个深度的电压串联负反馈电路。因为u_ = u+= uI，所以不存在“虚地”现象，在选用集成运放时要考虑到其输入端可能具有较高的共模输入电压。
2）电压放大倍数 
，即输出电压与输入电压的幅值成正比，且相位相同。也就是说，电路实现了同相比例运算。Auf也只取决于电阻RF和R1之比，而与集成运放的内部参数无关，所以比例运算的精度和稳定性主要取决于电阻RF和R1的精确度和稳定度。一般情况下，Auf值恒大于1。当RF=0或R1=∞时，Auf=1，这种电路称为电压跟随器。
3）由于引入深度电压串联负反馈，因此电路的输入电阻很高，输出电阻很低。
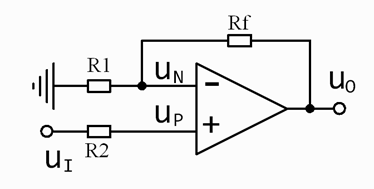
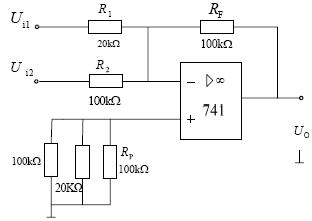
3、差分比例运算电路
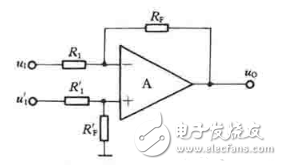
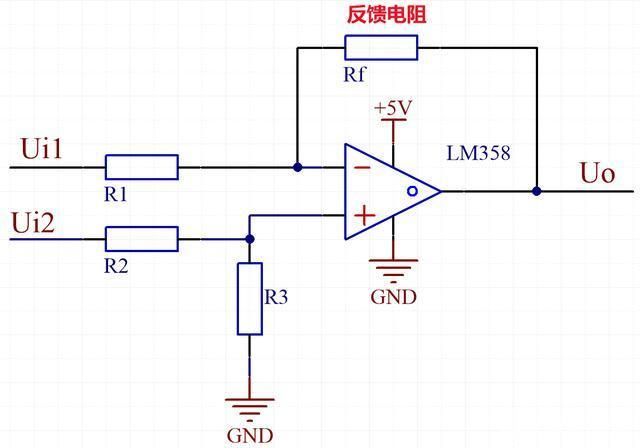
在上图中，输入电压uI和uI’分别加在集成运放的反相输入端和同相输入端，从输出端通过反馈电阴RF接回到反相输入端。为了保证运放两个输入端对地的电阻平衡，同时为了避免降低共模抑制比，通常要求
R1= R1’
RF= RF’
在理想条件下，由于“虚断”，i+=i_=0，利用叠加定理可求得反相输入端的电位为
而同相输入端的电位为
当满足条件R1 = R1’，RF = RF’ 时，整理上式，可求得差分比例运算电路的电压放大倍数为
（8）
在电路元件参数对称的条件下，差分比例运算电路的差模输入电阻为
Rif = 2R1 （9）
由式（8）可知，电路的输出电压与两个输入电压之差成正比，实现了差分比例运算。其比值旧|Auf|同样决定于电阻RF和R1之比，而与集成运放内部参数无关。由以上分析还可以知道，差分比例运算电路中集成运放的反相输入端和同相输入端可能加有较高的共模输入电压，电路中不存在“虚地”现象。
差分比例运算电路除了可以进行减法运算以外，还经常被用作测量放大器。差分比例运算电路的缺点是对元件的对称性要求比较高，如果元件失配，不仅在计算中带来附加误差，而且将产生共模电压输出。电路的另一个缺点是输入电阻不够高。
以上介绍了反相输入、同相输入和差分输入三种基本形式的比例电路，现将它们的电路组成、电压放大倍数、输入和输出电阻，以及性能特点归纳在表中，以便进行比较。
上述各种比例运算电路的输入、输出关系表达式都是在理想运放条件下得到的，但实际集成运放的各项指标不可能完全理想，因此在上述运算公式中将产生误差。
工商网监
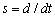
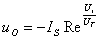
评论