德赢Vwin官网
App
MPU6050模块，如图 1所示。该模块集成了一片MPU6050芯片和一片STM8S003F3P6单片机，具有串口和I2C接口。MPU6050中的DMP（数字运动处理器）对姿态进行融合，STM8单片机通过IIC读取DMP的处理结果，再添加上包头串行输出三轴加速度、三轴角速度、三轴角度和温度数据，输出频率为100Hz。
MPU6050芯片内部由四部分组成：加速度计、陀螺仪、DMP（Digital Motion Processing）、温度传感器。DMP部分的Datasheet原文介绍：The DMPacquires data from accelerometers， gyroscopes， and additional 3rdparty sensorssuch as magnetometers， and processes the data. The resulting data can be readfrom the DMP’s registers， or can be buffered in a FIFO. The DMP has access toone of the MPU’s external pins， which can be used for generating interrupts.
陀螺仪误差分析
imu误差的效果
陀螺仪的偏移对于速度的影响是二次的，对于位置的影响是三次的。
对于收敛的并且设计很好的滤波器，估计和去除imu的误差，能够提高姿态的精度和长期稳定性
常见误差项：
首先介绍几个常见的概念：
1.重复性
假设所有的条件一样，对于相同的输入，传感器输出相同的值的能力（对于每次启动都相同）。陀螺仪的零偏不具有重复性。
2.稳定性
对于同样的输入，在同一次启动，输出值都是相同的。
3.漂移
输出随着时间的变化（零漂是输入为0的时候的输出）
确定性误差
传感器非正交性（安装误差）：
三轴加速度计和陀螺仪的三个轴不是完全的正交的，例如对于加速度计，理想情况下其中一个轴测量重力，其他两个轴不应该有输出。传感器不正交会出现在安装和封装的时候。生产和标定能够一定程度的解决这个问题，在系统运行的时候持续的估计和矫正也是一种解决方法。
尺度误差（scale）
随机噪声
《Notes on Stochastic Errors of Low Cost MEMS Inertial Units》
陀螺仪的噪声分析不适用arma模型，应该使用allan variance。
因为arma模型假设所有的误差都是完全客观的，然而在实际中：传感器的输出受到噪声的影响，而且是不同的独立随机过程的和；目前的arma模型能够解决噪声的影响，但是不能够解决独立随机过程的系数问题。误差中最主要的是：（1）零偏、温漂；（2）角速率噪声，也叫作随机游走
所有噪声可以建模为：
（1）y（t）=u（t）+e（t）+b（T）+N（a，ω，T，t）
allan variance 建模
b（T）表示温漂，一般不考虑，可以通过温度补偿来做
N（a，ω，T，t）表示加速度，角速度，温度和时间等总的因素造成的影响（
G 的依赖性（加速度影响），对于mems陀螺仪来说，有可能受到重力的影响，可以通过建模并采用一定的方法去除这个影响）
e（t）=ARW（t）+F（t）+Q（t）+S（t）表示随机噪声
陀螺仪的误差分类
a。量化噪声Q（t）（Quantization Noise）
AD采样导致的噪声，量化噪声具有很宽的带宽，属于高频噪声，可以用低通滤波器处理或通过导航的积分环节去除，对精度的影响不大；
量化噪声的分辨率为
Δ（和AD的位数有关系），采样频率为
f=1/τ（手册中会介绍采样的频率），τ为采样时间，则量化噪声的功率谱密度为
SΔ（f）=τ0Q2，Allan方差为
σQN2（τ）=3Q2τ2。
量化噪声属于高频噪声，在实际的应用中可进行低通滤波处理或大部分被导航的积分环节滤除。
b。角度随机游走（ARW（t））（Angular Random Walk）
高斯白噪声的影响，需要区别角速率输出还是角增量输出，mpu6050是角速度输出。
角度随机游走的功率谱密度为
SΩ（f）=N2，Allan方差为
σARW2（τ）=N2τ
一般陀螺仪内部会有低通滤波器。白噪声功率谱密度的等效带宽，叫作陀螺仪的带宽；（惯性仪器，157页））通过高频采样和低通滤波能够降低mems陀螺仪的角度随机游走噪声；
从另外一个角度分析：
假设每次测量的角速度受到白噪声的影响，即
δθk=δθ+Nk∗τ，其中Nk为独立同分布的零均值白噪声，标准差σ，则经过时间
n⋅τ之后，误差为
e=τ∑i=1nNi
从而e的数学特征为
E（e）=0，
Var（e）=δt2nVar（N）=δt⋅t⋅σ2
所以
σ（e）=σ⋅δt⋅t
因此，在手册中一般将上面的噪声常时间的积分的标准差记做
ARW=σθ（1）
单位为
∘/hc。零偏不稳定性（F（t））（Bias Instability） ，也叫作闪变噪声（Flicker Noise）
准确的来说，并不是只有零偏导致偏移，零偏是没有运动时平均输出。零偏不稳定性即零偏会随着时间缓慢的变化。这是由于内部电磁的善变噪声和外部影响导致的，而且每次启动之初的零偏是不相同的。
零偏不稳定性的功率谱为
SΩ（f）=B22πf，Allan方差为
σBI2（τ）=4B29
零偏的不稳定性描述一段时间之后，MEMS的零偏的变化情况。零偏稳定性通常定义为1σ值，单位为∘/h。举例来说，假设当前时刻的零偏是已知的
Bt，经过100s后，零偏的均值为Bt，标准差为
0.01∘/h。实际上，零漂并不是一个完全的随机游走，它的范围是有限的。零漂对角度的影响是线性的。
d。速率斜坡（Rate Ramp）
陀螺的角速率输出随着时间缓慢变化，通常由系统误差引起，比如环境温度的缓慢变化，可以通过严格的环境控制或引入补偿来降低此类误差。这个不应该存在，而且可以通过一定的措施去除掉。貌似就是b（T）温漂
温度补偿和温度闭环两种方法比较：温度补偿很难做，而且效果不好，一般使用温度闭环；
e。指数相关噪声（Exponential Correlation Noise）和正弦噪声S（t）（Sinusoidal Noise）
正弦噪声：由于mems单元在特定频率工作，所以一般受到正弦噪声的污染；
从算法上需要解决的：（1）角度随机游走（2）零偏不稳定性
MPU6050不论是做平衡还是四轴飞行器，关键的问题在于模块姿态的确定，通常需要用到积分运算与卡尔曼滤波算法，需要较强的数学功底与编程能力，因此以下主要分析姿态确定问题。
虽然6050芯片能够输出三轴加速度和三轴角速度的数据，但实际应用的时候，直接使用的确不是这些量，而是需要根据这些数据解算出三轴的角度数据。比如平衡小车，需要算出模块的俯仰角，然后控制算法根据角度大小控制小车轮子的移动。四轴飞行器需要根据俯仰角度、滚转角度，和飞行指令来调节四个电机的转速。
从6轴的原始数据得到三轴的角度计算是一个比较复杂的运动学解算过程，有三点需要注意的问题：
1.三轴姿态的解算不能直接积分。因为三轴是有耦合的，只有在三轴角度为小角度的时候可以这么算，角度大了以后，比如60度了，这么算的误差就很大。标准的做法是用四元数的方法做姿态解算，积分的方法可以用4阶龙格-库塔法，或者4阶Gill法。详情请参考：航空航天器运动的建模——飞行动力学的理论基础肖业伦著北京航空航天大学出版社。
2.积分运算的累积误差。角速度积分运算是有累积误差的，累积误差在短时间内表现不明显，只要零点漂移处理得好了，1分钟以内的漂移都不大，但时间长了，就会有累积误差。稳像仪中使用的MPU6050模块零点漂移比较小，5分钟大概0.02度。
3.角速率零点漂移。所谓零点漂移就是模块静止的时候，我们认为正常的输出应该是0，或者均值为0的数据，但是实际上6050的输出不是，经测量，小于0.15度/秒。
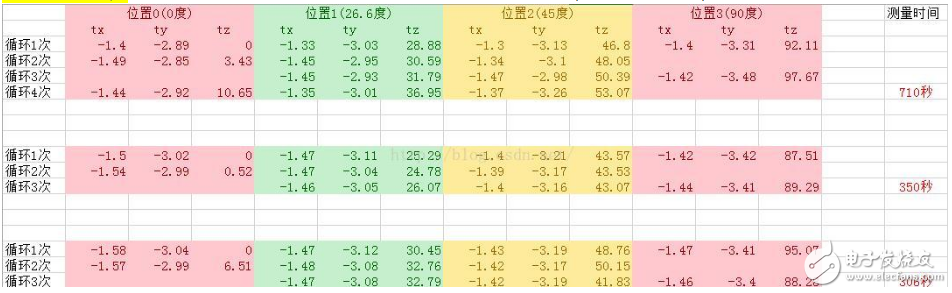
在纸上画出四个角度，分别为0度、26.6度、45度、90度，将纸固定在桌子上，每次将陀螺仪模块旋转到对应的位置，经过多次实验（实验结果如图2所示），证实所使用的MPU6050模块的角度输出确实存在很大的误差。但是从datasheet上看，MPU6050芯片和其他精度高且价格昂贵的芯片如ADIS16系列差别不是大，那么极有可能是姿态融合算法部分的问题。MPU6050模块的姿态融合是在STM8单片机中实现的，而且没有源码，精度难以保证。
综上所述，有两种解决方法：
一、使用MPU6050模块输出的角速度和加速度的原始数据，用算法对其进行姿态融合，得到角度。综合利用陀螺仪和加速度计的特点，优势互补获得准确的姿态角度，方法就是用卡尔曼滤波做数据融合。大致的思路是将模块的姿态用四元素表示，作为系统的状态量，模块的姿态运动学方程作为滤波的状态转移方程，加速度信息作为滤波的观察量信息，然后利用卡尔曼滤波的计算方法迭代计算更新，详细的过程可以参考惯性导航方面的书籍。不过卡尔曼滤波算法比较复杂，需要用到矩阵运算等等，而且MPU6050模块是IIC接口输出的。
二、采用更高精度的陀螺仪模块，直接得到角度。
工商网监
评论