德赢Vwin官网
App
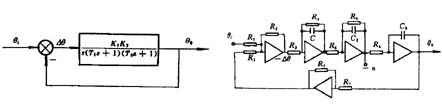
根据数学模型的相似原理，我们应用电子元件模拟工程系统中的典型环节，然后加入典型测试信号，测试环节的输出响应。反之从实测的输出响应也可以求得未知环节的传递函数及其各个参数。
模拟典型环节传递函数的方法有两种：第一种方法，利用模拟装置中的运算部件，采用逐项积分法，进行适当的组合，构成典型环节传递函数模拟结构图；第二种方法将运算放大器与不同的输入网络、反馈网络组合，构成传递函数模拟线路图，这种方法可以称为复合网络法。本节介绍第二种方法。
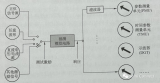
| (a)模拟电路 | (b)输出响应 |
| 图2-3-1惯性环节的模拟电路及响应 |
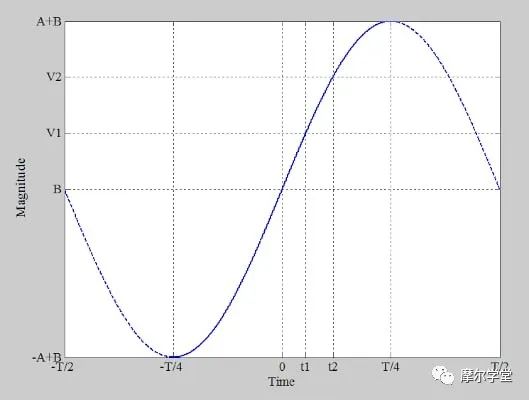
当输入负阶跃信号时，其输出响应如图2-3-1(b)所示。从图中可知，T和K是响应曲线的两个特征量。T表示阶跃信号输入后，响应按指数上升的快慢，它可从响应曲线实测得到。
 |
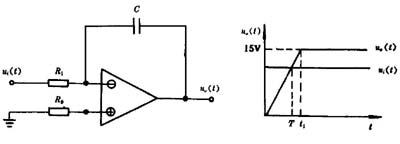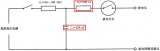
| (a)模拟电路 | (b)输出响应 |
| 图2-3-2 积分环节的模拟电路及响应 |
当输入负阶跃信号时，其输出响应如图2-3-2(b)所示。从图中可知，积分时间常数Ti是积分环节的特征量，它表示阶跃输入后响应按线性上升的快慢，Ti可从响应曲线上求出，即响应上升到阶跃输入幅值时所需的时间。积分环节的特点是，不管输入幅值多小，输出就不断地按线性增长，输入幅值愈小，增长的速率愈小，只有输入为零时，输出才停止增长而保持其原来的数值。从图中可看出运算放大器最终达到饱和值。
| (a)模拟电路 | (b)输出响应 |
| 图2-3-3 比例积分环节的模拟电路及响应 |
当输入负阶跃信号时，其输出响应如图2-3-3(b)所示。从该图中可以得到比例积分环节的特征参数K和Ti。必须注意：在测试积分环节和比例积分环节的阶跃响应时，由于存在储能元件C，因此每次输入阶跃响应时，必须保证uc为零，否则将因uc的初始值不同使每次测得的响应不同。
| (a)模拟电路 | (b)输出响应 |
| 图2-3-4 比例积分微分环节的模拟电路及理想的响应 |
对于理想的比例积分微分环节，当输入负阶跃信号时其输出响应如图2-3-4(b)所示，在输入跃变时，它的输出响应能够以无限大的变化率在瞬间跃至∞ ，又在此瞬间下降至按某一比例Kp分配的电压值，并立即按积分时间常数Ti规律线性增长。而模拟比例积分微分环节的输出响应，在输入跃变时只能以有限的变化率上升至运算放大的饱和值就不再增长，经过一段时间，又以有限的变化率下降。这是因为模拟电路是在满足R1>>R3 、C21>>C1 的条件下，忽略了小时间常数才得到近似的PID数学模型式，而且运算放大器也不是理想的，因此实际比例积分微分环节的响应曲线与图2-3-4(b)略有不同。
综上所述，典型环节的模拟方法是：根据典型环节的传递函数，选择适当的网络作为运算放大器的输入阻抗与反馈阻抗，使模拟电路的传递函数与被模拟环节的传递函数具有同一表达式，然后根据被模拟环节传递函数的参数，计算出模拟电路各元件的参数值。
工商网监
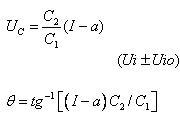
评论